2023年中考苏科版数学一轮复习专题讲义与练习-全等图形

这是一份2023年中考苏科版数学一轮复习专题讲义与练习-全等图形，共4页。
【课标要求】
1.熟悉全等图形的基本性质；
2.熟练掌握三角形全等的概念和两个三角形全等的条件；并能熟练运用全等三角形的性质和判定进行相关的计算和证明；
3.熟悉角平分线的性质和判定，会用直尺和圆规作角的平分线；
4.了解三角形的稳定性.
【要点梳理】
1. 叫做全等图形， 叫做全等三角形；
2.全等三角形的 相等， 相等；
3.全等三角形的条件：
（1） , 简写成 ；
（2） , 简写成 ；
（3） _ , 简写成 ；
（4） , 简写成 ；
4.直角三角形全等的判定定理
5.角平分线的性质定理： , 角平分线的判定定理： ；
6.三角形具有 性，四边形具有 性.
【规律总结】
1.灵活应用全等三角形的条件证题，常见思路有：
（1）已知两边：①找夹角SAS；②找直角HL；③找另一边SSS；
（2）已知一边一角：①边为角的对边找另外任一角AAS；
②边为角的邻边
（3）已知两角
2.全等三角形的应用;若两个三角形全等，则它们的对应边.对应角相等，因此我们常常利用全等三角形来证明线段和角相等.
3.全等三角形的其他对应线段都相等（证明方法，适用范围）
【强化训练】
1.如图，点在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（ ）
A．∠A＝∠DB．AC＝DFC．AB＝EDD．BF＝EC
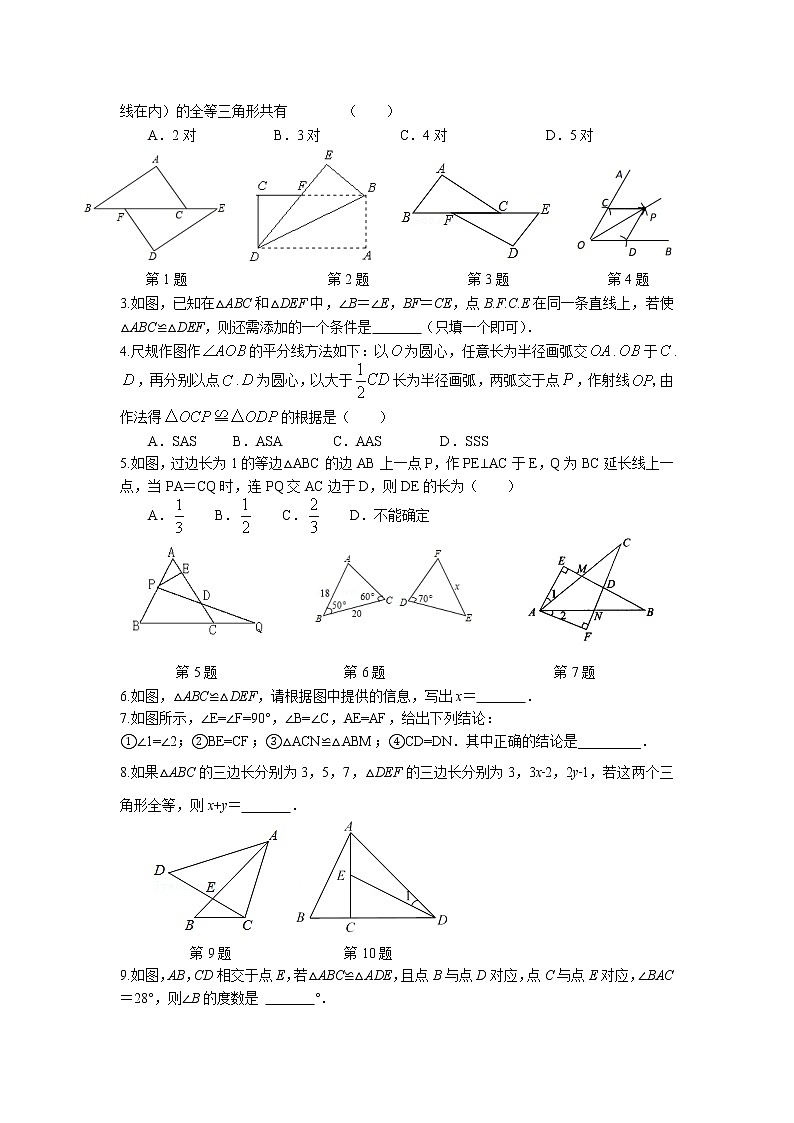
2.如图，△BDE是将长方形纸片ABCD沿对角线BD折叠后得到的，则图中（包括实线.虚线在内）的全等三角形共有（ ）
A．2对 B．3对 C．4对 D．5对

第1题 第2题 第3题 第4题
3.如图，已知在△ABC和△DEF中，∠B＝∠E，BF＝CE，点在同一条直线上，若使△ABC≌△DEF，则还需添加的一个条件是 （只填一个即可）．
4.尺规作图作的平分线方法如下：以为圆心，任意长为半径画弧交.于.，再分别以点.为圆心，以大于长为半径画弧，两弧交于点，作射线由作法得的根据是（ ）
A．SAS B．ASA C．AAS D．SSS
5.如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为（ ）
A． B． C． D．不能确定
第5题 第6题 第7题
6.如图，△ABC≌△DEF，请根据图中提供的信息，写出x＝ ．
7.如图所示，∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：
①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论是_________．
8.如果△ABC的三边长分别为3，5，7，△DEF的三边长分别为3，3x﹣2，2y﹣1，若这两个三角形全等，则x+y＝ ．

第9题 第10题
9.如图，AB，CD相交于点E，若△ABC≌△ADE，且点B与点D对应，点C与点E对应，∠BAC＝28°，则∠B的度数是 °．
10.如图，已知Rt△ABC≌Rt△DEC，连结AD，若∠B＝58°，则∠1的度数是 ．
11.沿着图中的虚线，用四种不同的方法将下面的图形分成个全等的图形
12.如图，已知△ABC≌△DEB，点E在AB上，DE与AC相交于点F，
（1）当DE=8，BC=5时，线段AE的长为_________；
（2）已知∠D=35°，∠C=60°，
①求∠DBC的度数；
②求∠AFD的度数．
13.如图，∠A＝∠B，AE＝BE，点D在AC边上，∠1＝∠2，AE和BD相交于点O．
（1）求证：△AEC≌△BED；
（2）若∠1＝42°，求∠BDE的度数．
14.如图①，在Rt△ABC中，∠C＝90°，BC＝9cm，AC＝12cm，AB＝15cm，现有一动点P，从点A出发，沿着三角形的边AC→CB→BA运动，回到点A停止，速度为3cm/s，设运动时间为ts．
（1）如图（1），当t＝ 时，△APC的面积等于△ABC面积的一半；
（2）如图（2），在△DEF中，∠E＝90°，DE＝4cm，DF＝5cm，∠D＝∠A．在△ABC的边上，若另外有一个动点Q，与点P同时从点A出发，沿着边AB→BC→CA运动，回到点A停止．在两点运动过程中的某一时刻，恰好△APQ≌△DEF，求点Q的运动速度．
15.如图，在△ACD中，E为边CD上一点，F为AD的中点，过点A作AB∥CD，交EF的延长线于点B．
（1）求证：△AFB≌△DFE；
（2）若AB＝6，DC＝4CE，求CD的长．
16.（1）如图1，图2，图3，在△ABC中，分别以AB，AC为边，向△ABC外作正三角形，正四边形，正五边形，BE，CD相交于点O．
①如图1，求证：△ABE≌△ADC；
②探究：如图1，∠BOC＝ ；如图2，∠BOC＝ ；如图3，∠BOC＝ ；
（2）如图4，已知：AB，AD是以AB为边向△ABC外所作正n边形的一组邻边；AC，AE是以AC为边向△ABC外所作正n边形的一组邻边，BE，CD的延长相交于点O．
①猜想：如图4，∠BOC＝ （用含n的式子表示）；
②根据图4证明你的猜想．