人教版八年级下册17.1 勾股定理精品课件ppt

这是一份人教版八年级下册17.1 勾股定理精品课件ppt，共17页。PPT课件主要包含了复习回顾，问题1，几何语言，新知探究，探究一，问题2，木板可以斜着过吗，探究二，∴OB1，≈57m等内容，欢迎下载使用。
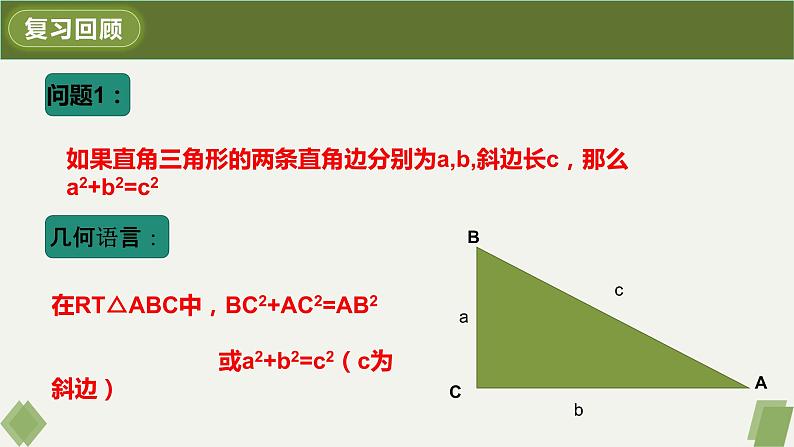
如果直角三角形的两条直角边分别为a,b,斜边长c，那么a2+b2=c2
在RT△ABC中，BC2+AC2=AB2 或a2+b2=c2（c为斜边）
木板可以横着过吗？可以竖着过吗？
分析：可以看出，木板横着或竖着都不能从门框通过，只能试试斜着能否通过。门框对角线AC的长度是斜着能通过的最大长度。求出AC，再与木板的宽度比较，就能知道木板能否通过。
例1：一个门框的尺寸如图所示，一块长3 m，宽2.2 m的长方形薄木板能否从门框内通过？为什么？
根据题意, 画出图形.
解：在Rt△ABC中，根据勾股定理，
因为AC大于木板的宽2.2m,所以木板能从门框内通过.
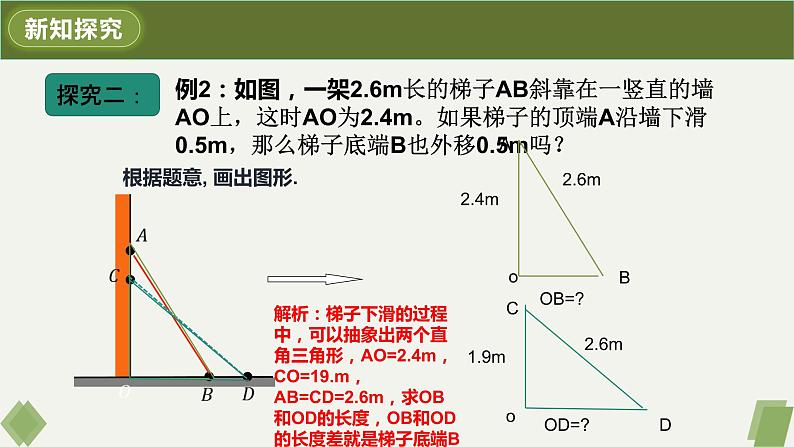
例2：如图，一架2.6m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2.4m。如果梯子的顶端A沿墙下滑0.5m，那么梯子底端B也外移0.5m吗？
解析：梯子下滑的过程中，可以抽象出两个直角三角形，AO=2.4m，CO=19.m，AB=CD=2.6m，求OB和OD的长度，OB和OD的长度差就是梯子底端B外移的距离。
解：在Rt△AOB中，根据勾股定理得
OB2=AB2-OA2=2.62-2.42=1，
在Rt△COD中，根据勾股定理得
OD2=CD2-OC2=2.62-(2.4-0.5)2=3.15,
∴梯子的顶端沿墙下滑0.5m时，梯子底端并不是也外移0.5m，而是外移约0.77m.
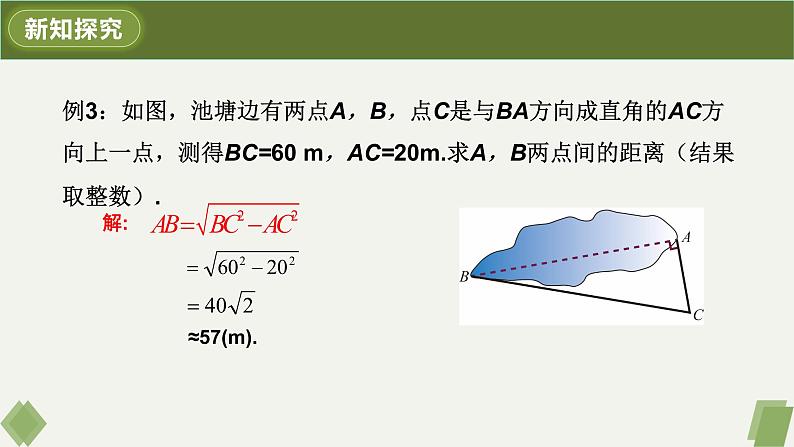
例3：如图，池塘边有两点A，B，点C是与BA方向成直角的AC方向上一点，测得BC=60 m，AC=20m.求A，B两点间的距离（结果取整数）.
例4：在《九章算术》中有一个问题（如图）：今有竹高一丈，末折抵地，去本三尺，问折者高几何？它的意思是：一根竹子原高一丈（10尺），中部一处折断，竹梢触地面处离竹根3尺，试问折断处离地面几尺．
解：如图，由题意得：∠ACB＝90°，BC＝3尺，AC+AB＝10尺，设折断处离地面x尺，则AB＝（10﹣x）尺，在Rt△ABC中，由勾股定理得：x2+32＝（10﹣x）2，解得：x＝4.55，即折断处离地面4.55尺．
【分析】根据题意作出图形，设折断处离地面x尺，则AB＝（10﹣x）尺，勾股定理求解即可。
3.如图，有两棵树，一棵高19米，另一棵高10米，两树相距12米．若一只小鸟从一棵树的树梢飞到另一棵树的树梢，则小鸟至少飞行（ ）A．10米B．15米C．16米D．20米
4.如图，有两棵树，一棵高8米，另一棵高2米，两树相聚8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少飞了（　　）米．A．7B．8C．9D．10
5.如图，一棵大树（树干与地面垂直）在一次强台风中于离地面6米B处折断倒下，倒下后的树顶C与树根A的距离为8米，则这棵大树在折断前的高度为（ ）A．10米B．12米C．14米D．16米
利用勾股定理解决实际问题的基本步骤：
（1）读懂题意，分析已知、未知间的关系；
（2）构造直角三角形；
（3）利用勾股定理等列方程；