初中数学人教版八年级下册18.2.2 菱形精品ppt课件

这是一份初中数学人教版八年级下册18.2.2 菱形精品ppt课件，共23页。PPT课件主要包含了平行四边形，归纳总结，菱形的性质，相等的线段，相等的角，等腰三角形有，直角三角形有，全等三角形有，菱形ABCD中，菱形的面积等内容，欢迎下载使用。
学习目标1. 探索并证明菱形的性质定理. 2. 应用菱形的性质定理解决相关计算或证明问题．
思考：如果从边的角度，将平行四边形特殊化，内角大小保持不变仅改变边的长度让它有一组邻边相等，这个特殊的平行四边形叫什么呢?
菱形是特殊的平行四边形.
平行四边形不一定是菱形.
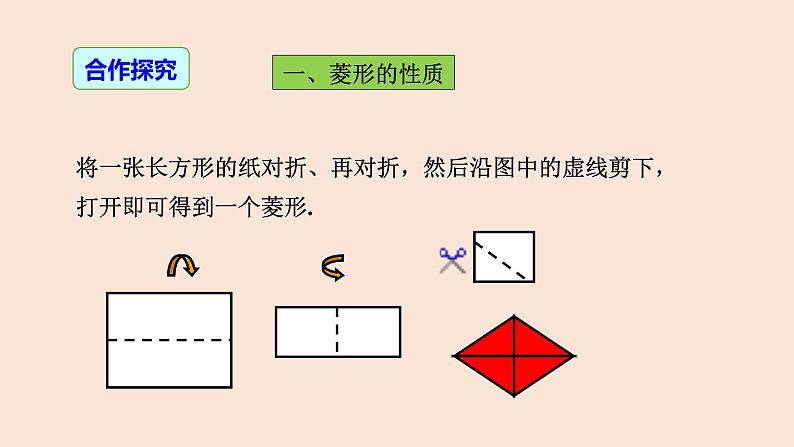
将一张长方形的纸对折、再对折，然后沿图中的虚线剪下，打开即可得到一个菱形.
画出菱形的两条折痕，并通过折叠手中的图形回答以下问题：
1. 菱形是轴对称图形吗？
2. 菱形有几条对称轴？
3. 对称轴之间有什么关系？
4. 你能看出图中哪些线段和角相等？
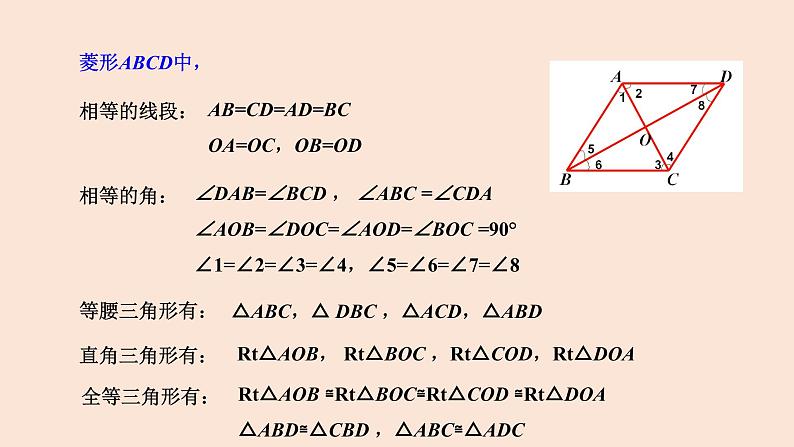
AB=CD=AD=BC OA=OC，OB=OD
∠DAB=∠BCD ， ∠ABC =∠CDA ∠AOB=∠DOC=∠AOD=∠BOC =90° ∠1=∠2=∠3=∠4，∠5=∠6=∠7=∠8
△ABC，△ DBC ，△ACD，△ABD
Rt△AOB， Rt△BOC ，Rt△COD，Rt△DOA
Rt△AOB ≌Rt△BOC≌Rt△COD ≌Rt△DOA△ABD≌△CBD ，△ABC≌△ADC
菱形是特殊的平行四边形，具有平行四边形的所有性质.
由此我们可以得到菱形的性质：
菱形是轴对称图形， 对称轴有两条，是菱形两条对角线所在的直线.
问题：猜想菱形的四条边在数量上有什么关系？ 菱形的两条对角线有什么关系？
猜想1：菱形的四条边都相等.
猜想2：菱形的两条对角线互相垂直，并且每一条对角线平分一组对角.
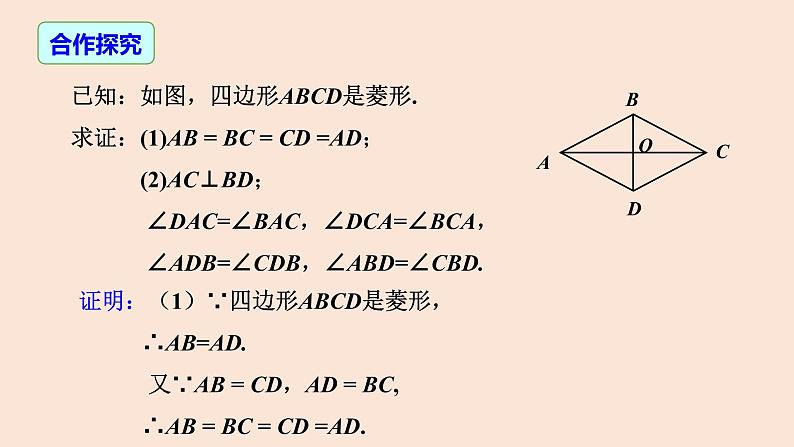
已知：如图，四边形ABCD是菱形. 求证：(1)AB = BC = CD =AD； (2)AC⊥BD； ∠DAC=∠BAC，∠DCA=∠BCA， ∠ADB=∠CDB，∠ABD=∠CBD.
证明：（1）∵四边形ABCD是菱形， ∴AB=AD. 又∵AB = CD，AD = BC, ∴AB = BC = CD =AD.
（2）∵AB = AD, ∴△ABD是等腰三角形. 又∵四边形ABCD是菱形, ∴OB = OD . 在等腰三角形ABD中， ∵OB = OD， ∴AO⊥BD，AO平分∠BAD， 即AC⊥BD，∠DAC=∠BAC. 同理可证∠DCA=∠BCA， ∠ADB=∠CDB，∠ABD=∠CBD.
例1：如图，在菱形ABCD中，CE⊥AB于点E，CF⊥AD于点F，求证：AE＝AF.
证明：连接AC. ∵四边形ABCD是菱形， ∴AC平分∠BAD， 即∠BAC＝∠DAC. ∵CE⊥AB，CF⊥AD， ∴∠AEC＝∠AFC＝90°. 又∵AC＝AC， ∴△ACE≌△ACF. ∴AE＝AF.
问题1：菱形是特殊的平行四边形，那么能否利用平行四边形面积公式计算菱形ABCD的面积吗?
思考：前面我们已经学习了菱形的对角线互相垂直，那么能否利用对角线来计算菱形ABCD的面积呢?
能.过点A作AE⊥BC于点E,则S菱形ABCD=底×高 =BC·AE.
问题2：如图，四边形ABCD是菱形，对角线AC，BD交于点O，试用对角线表示出菱形ABCD的面积.
解：∵四边形ABCD是菱形，∴AC⊥BD，∴S菱形ABCD=S△ABC +S△ADC= AC·BO+ AC·DO= AC(BO+DO)= AC·BD.
菱形的面积 = 底×高 = 对角线乘积的一半
例2：如图，在菱形ABCD中，点O为对角线AC与BD的交点，且在△AOB中，OA＝5，OB＝12.求菱形ABCD两对边的距离h.
解：在Rt△AOB中，OA＝5，OB＝12，∴S△AOB＝ OA·OB＝ ×5×12＝30，∴S菱形ABCD＝4S△AOB＝4×30＝120.又∵菱形两组对边的距离相等，∴S菱形ABCD＝AB·h＝13h，∴13h＝120，得h＝ .
1. 如图，在菱形ABCD中，已知∠A＝60°，AB＝5，则△ABD的周长是 （ ） A.10 B.12 C.15 D.20
2. 如图，菱形ABCD的周长为48cm，对角线AC、BD相交于O点，E是AD的中点，连接OE，则线段OE的长为_______.
3. 如图，已知菱形的两条对角线长分别为6cm和8cm，则这个菱形的高DE为（　　） A. 2.4cm B. 4.8cm C. 5cm D. 9.6cm
4. 如图，四边形ABCD是边长为13cm的菱形，其中对角线BD长10cm.
求：(1)对角线AC的长度; (2)菱形ABCD的面积.
∵四边形ABCD是菱形，
(2)菱形ABCD的面积
∴AC=2AE=2×12=24(cm).
5. 如图，O是菱形ABCD对角线AC与BD的交点，CD＝5cm，OD＝3cm；过点C作CE∥DB，过点B作BE∥AC，CE与BE相交于点E.(1)求OC的长；(2)求四边形OBEC的面积．
解：(1)∵四边形ABCD是菱形，∴AC⊥BD.在Rt△OCD中，由勾股定理得OC＝4cm.(2)∵CE∥DB，BE∥AC，∴四边形OBEC为平行四边形.又∵AC⊥BD，即∠COB＝90°，∴平行四边形OBEC为矩形.∵OB＝OD＝3cm，∴S矩形OBEC＝OB·OC＝4×3＝12(cm2)．
1.（3分）（2021•河南6/23）关于菱形的性质，以下说法不正确的是（ ） A．四条边相等 B．对角线相等 C．对角线互相垂直 D．是轴对称图形
【解答】解：A、菱形的四条边相等，正确，不符合题意，B、菱形的对角线互相垂直且平分，对角线不一定相等，不正确，符合题意，C、菱形的对角线互相垂直且平分，正确，不符合题意，D、菱形是轴对称图形，正确，不符合题意，故选：B．
2.（3分）（2021•西藏9/27）已知一元二次方程x2-10x+24=0的两个根是菱形的两条对角线长，则这个菱形的面积为（ ） A．6B．10 C．12 D．24
3.（3分）（2021•山西13/23）如图，在菱形ABCD中，对角线AC，BD相交于点O，BD=8，AC=6，OE∥AB，交BC于点E，则OE的长为 ．
【分析】由菱形的性质可得：AO=3，BO=4，AC⊥BD，借助勾股定理求出AB=5，再证明OE是△ABC的中位线即可求解．
1.周长=边长的四倍2.面积=底×高=两条对角线乘积的一半
1.两组对边平行且相等；2.四条边相等
两组对角分别相等，邻角互补
1.两条对角线互相垂直平分；2.每一条对角线平分一组对角