



所属成套资源:宁夏回族自治区银川一中2022-2023学年高三下学期第一次模拟考试
宁夏回族自治区银川一中2022-2023学年高三下学期第一次模拟考试数学(文)试题
展开这是一份宁夏回族自治区银川一中2022-2023学年高三下学期第一次模拟考试数学(文)试题,文件包含宁夏回族自治区银川一中2023届高三下学期第一次模拟考试数学文试题解析版docx、宁夏回族自治区银川一中2023届高三下学期第一次模拟考试数学文试题原卷版docx等2份试卷配套教学资源,其中试卷共26页, 欢迎下载使用。
1. 以下四个写法中:① ;②;③;④,正确的个数有( )
A. 个B. 个C. 个D. 个
2. 复数的共轭复数在复平面上对应的点在( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
3. 已知点,则满足下列关系式的动点的轨迹是双曲线的上支的是( )
A. B.
C. D.
4. 图为一个开关阵列,每个开关只有“开”和“关”两种状态,按其中一个开关次,将导致自身和所有相邻的开关改变状态.例如,按将导致,,,,改变状态.如果要求只改变的状态,则需按开关的最少次数为( )
A B. C. D.
5. 对件样品进行编号,,,,在如下随机数表中,指定从第行第列开始,从左往右抽取两个数字,抽取个编号,则抽到的第个编号是( )
A. B. C. D.
6. 是的( )
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
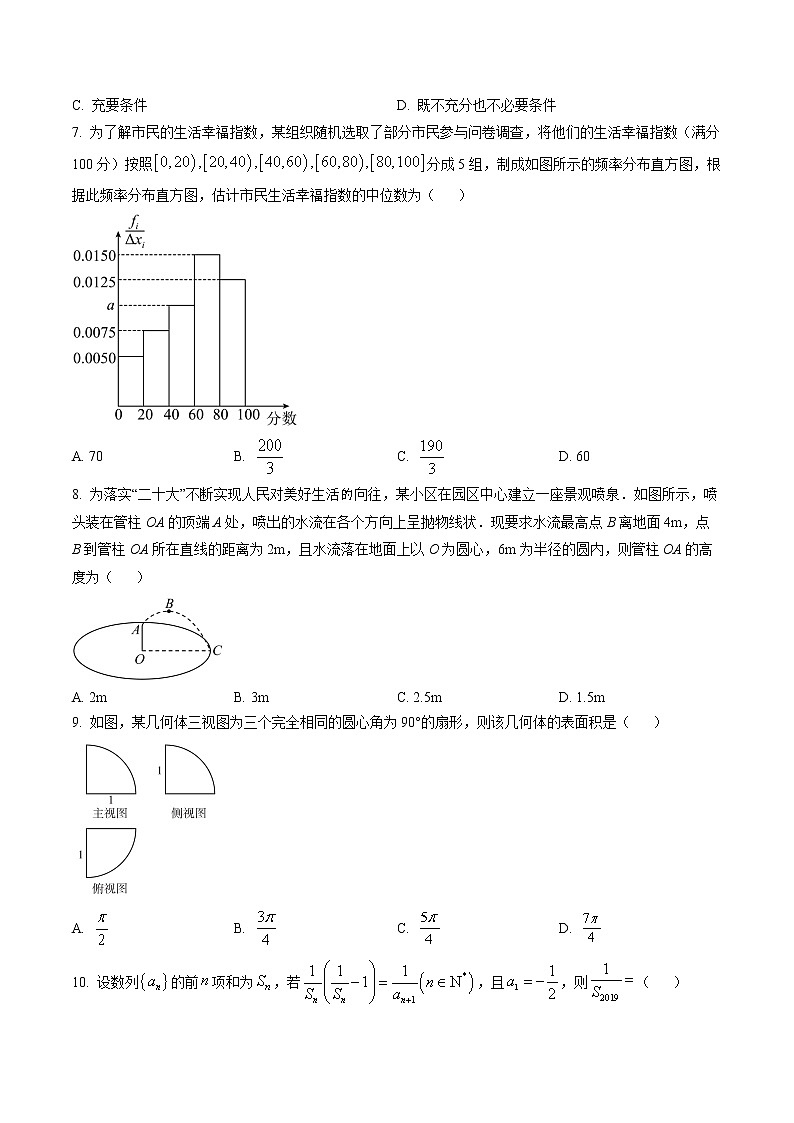
7. 为了解市民的生活幸福指数,某组织随机选取了部分市民参与问卷调查,将他们的生活幸福指数(满分100分)按照分成5组,制成如图所示的频率分布直方图,根据此频率分布直方图,估计市民生活幸福指数的中位数为( )
A. 70B. C. D. 60
8. 为落实“二十大”不断实现人民对美好生活向往,某小区在园区中心建立一座景观喷泉.如图所示,喷头装在管柱OA的顶端A处,喷出的水流在各个方向上呈抛物线状.现要求水流最高点B离地面4m,点B到管柱OA所在直线的距离为2m,且水流落在地面上以O为圆心,6m为半径的圆内,则管柱OA的高度为( )
A. 2mB. 3mC. 2.5mD. 1.5m
9. 如图,某几何体三视图为三个完全相同的圆心角为90°的扇形,则该几何体的表面积是( )
A. B. C. D.
10. 设数列的前项和为,若,且,则( )
A. 2019B. C. 2020D.
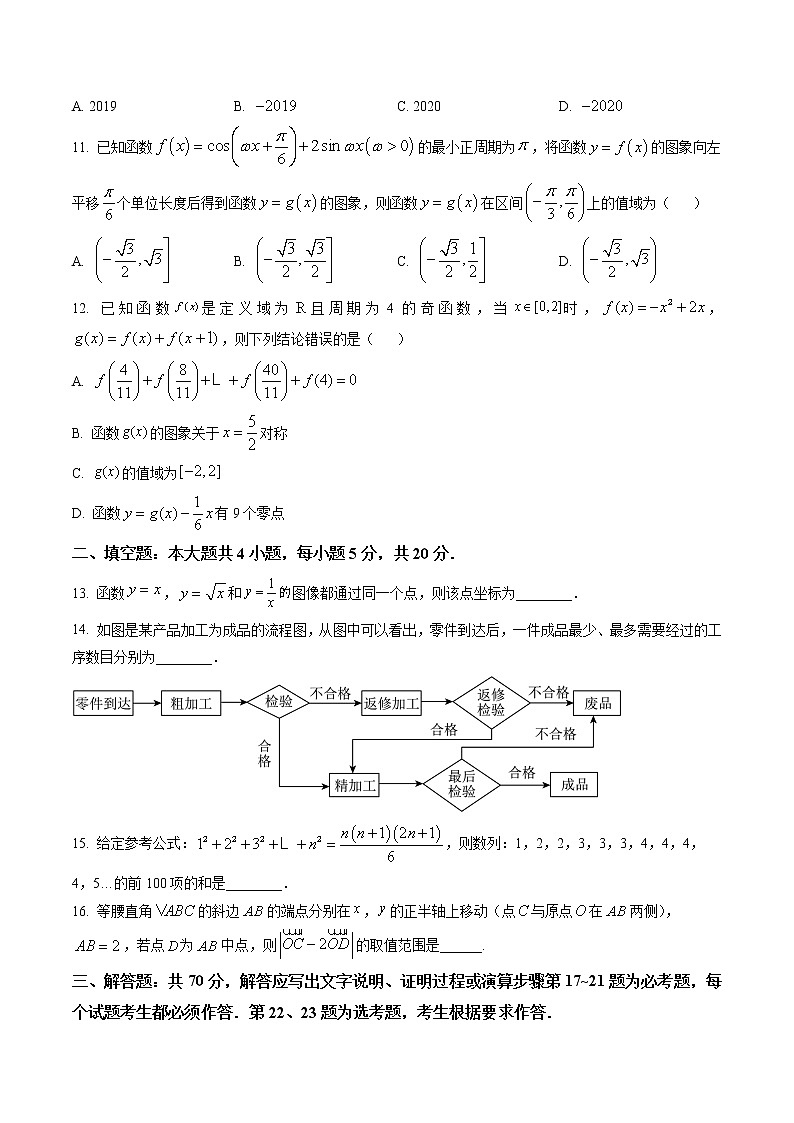
11. 已知函数的最小正周期为,将函数的图象向左平移个单位长度后得到函数的图象,则函数在区间上的值域为( )
A. B. C. D.
12. 已知函数是定义域为且周期为4的奇函数,当时,,,则下列结论错误的是( )
A.
B. 函数的图象关于对称
C. 的值域为
D. 函数有9个零点
二、填空题:本大题共4小题,每小题5分,共20分.
13. 函数,和图像都通过同一个点,则该点坐标为________.
14. 如图是某产品加工为成品的流程图,从图中可以看出,零件到达后,一件成品最少、最多需要经过的工序数目分别为________.
15. 给定参考公式:,则数列:1,2,2,3,3,3,4,4,4,4,5…的前100项的和是________.
16. 等腰直角的斜边的端点分别在,的正半轴上移动(点与原点在两侧),,若点为中点,则的取值范围是______.
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分
17. 设某幼苗从观察之日起,第x天的高度为y cm,测得的一些数据如下表所示:
作出这组数据的散点图发现:y(cm)与x(天)之间近似满足关系式,其中a,b均为大于0的常数.
(1)试借助一元线性回归模型,根据所给数据,用最小二乘法对,作出估计,并求出关于x的经验回归方程;
(2)在作出的这组数据的散点图中,甲同学随机圈取了其中的2个点,求这2个点中幼苗的高度大于的点的个数恰为1的概率.
附:对于一组数据,其回归直线方程的斜率和截距的最小二乘估计分别为,.
18. 已知三棱锥的侧棱,.且为靠近的三等分点.
(1)证明:;
(2)求点到平面的距离.
19. 重庆某公园有两块三角形草坪,准备修建三角形道路(不计道路宽度),道路三角形项点分别在草坪三角形的三条边上.
(1)第一块草坪三条边米,米,米,若,(如左图),区域内种植郁金香,求郁金香种植面积.
(2)第二块草坪的三条边米,米,米,为中点,(如右图),区域内种植紫罗兰,求紫罗兰种植面积的最小值.
20. 如图所示,由半椭圆和两个半圆、组成曲线,其中点依次为的左、右顶点,点为的下顶点,点依次为的左、右焦点.若点分别为曲线的圆心.
(1)求的方程;
(2)若过点作两条平行线分别与和交与和,求的最小值.
21. 已知函数的图像与直线相切于点.
(1)求函数的图像在点处的切线在x轴上的截距;
(2)求与的函数关系;
(3)当为函数的零点时,若对任意,不等式恒成立.求实数的取值范围.
(二)选考题:共10分.请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题记分.
[选修4—4:坐标系与参数方程]
22. 如图,在极坐标系Ox中,点,曲线M是以OA为直径,为圆心的半圆,点B在曲线M上,四边形OBCD是正方形.
(1)当时,求B,C两点的极坐标;
(2)当点B在曲线M上运动时,求D点轨迹的极坐标方程.
[选修4—5:不等式选讲]
23. 已知.
(1)若均为正数,证明,并且写出等号成立的条件;
(2)若,且恒成立,求的取值范围;第x天
1
4
9
16
25
36
49
高度y cm
0
4
7
9
11
12
13
相关试卷
这是一份宁夏回族自治区银川一中2023届高三第四次模拟考试数学(文)试题(含解析),共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份宁夏回族自治区银川一中2023届高三三模数学(文)试题,共6页。
这是一份宁夏回族自治区银川一中2022-2023学年高三下学期第四次模拟考试数学(文、理)试题,文件包含宁夏回族自治区银川一中2023届高三第四次模拟考试文科数学试题pdf、宁夏回族自治区银川一中2023届高三第四次模拟考试理科数学试题pdf等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。













