




高中数学人教A版 (2019)必修 第二册10.3 频率与概率优秀课后作业题
展开一、单选题
1.某同学做立定投篮训练,共两场,第一场投篮20次的命中率为80%,第二场投篮30次的命中率为70%,则该同学这两场投篮的命中率为( )
A.72%B.74%C.75%D.76%
【解析】该同学这两场投篮的命中率为.
故选:B.
2.在进行n次反复试验中,事件A发生的频率为,当n很大时,事件A发生的概率与的关系是( )
A.B.
C.D.
【解析】在进行n次反复试验中,事件A发生的频率为,当n很大时,越来越接近于,
所以可以用近似的代替,即,
故选:A
3.甲、乙两人做游戏,下列游戏中不公平的是( )
A.抛一枚骰子,向上的点数为奇数则甲胜,向上的点数为偶数则乙胜
B.同时抛两枚相同的骰子,向上的点数之和大于7则甲胜,否则乙胜
C.从一副不含大、小王的扑克牌中抽一张,扑克牌是红色则甲胜,是黑色则乙胜
D.甲、乙两人各写一个数字,若是同奇或同偶则甲胜,否则乙胜
【解析】A项,P(点数为奇数)=P(点数为偶数)=;
B项,P(点数之和大于7)=,P(点数之和小于等于7)=;
C项,P(牌色为红)=P(牌色为黑)=;
D项,P(同奇或同偶)=P(奇偶不同)=.
故选:B.
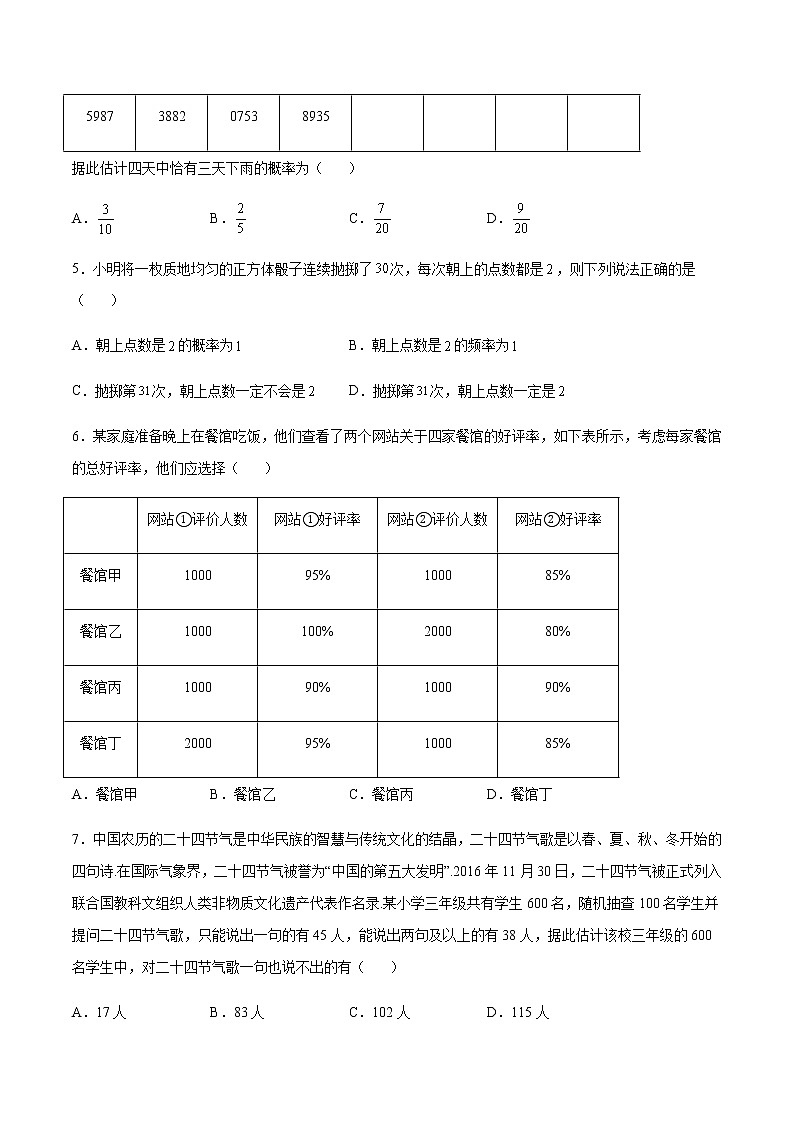
4.池州九华山是著名的旅游胜地.天气预报8月1日后连续四天,每天下雨的概率为0.6,现用随机模拟的方法估计四天中恰有三天下雨的概率:在0~9十个整数值中,假定0,1,2,3,4,5表示当天下雨,6,7,8,9表示当天不下雨.在随机数表中从某位置按从左到右的顺序读取如下20组四位随机数:
据此估计四天中恰有三天下雨的概率为( )
A.B.C.D.
【解析】由表中数据可得四天中恰有三天下雨的有9533,9522,0018,0018,3281,8425,2436,0753,共8组,所以估计四天中恰有三天下雨的概率为.
故选:B.
5.小明将一枚质地均匀的正方体骰子连续抛掷了次,每次朝上的点数都是,则下列说法正确的是( )
A.朝上点数是的概率为B.朝上点数是的频率为
C.抛掷第次,朝上点数一定不会是D.抛掷第次,朝上点数一定是
【解析】小明将一枚质地均匀的正方体骰子连续抛掷了30次,每次朝上的点数都是2,则朝上的点数是2的频率为,故选项B正确;
抛掷一枚质地均匀的正方体骰子,朝上的点数是2的概率为,故选项A错误;
抛掷第31次,朝上点数可能是2,也可能不是2,故选项C、D错误.
故选:B.
6.某家庭准备晚上在餐馆吃饭,他们查看了两个网站关于四家餐馆的好评率,如下表所示,考虑每家餐馆的总好评率,他们应选择( )
A.餐馆甲B.餐馆乙C.餐馆丙D.餐馆丁
【解析】餐馆甲的总好评率为:,
餐馆乙的总好评率为:,
餐馆丙的好评率为:,
餐馆丁的好评率为:,
显然,所以餐馆丁的总好评率最高.
故选:D
7.中国农历的二十四节气是中华民族的智慧与传统文化的结晶,二十四节气歌是以春、夏、秋、冬开始的四句诗.在国际气象界,二十四节气被誉为“中国的第五大发明”.2016年11月30日,二十四节气被正式列入联合国教科文组织人类非物质文化遗产代表作名录.某小学三年级共有学生600名,随机抽查100名学生并提问二十四节气歌,只能说出一句的有45人,能说出两句及以上的有38人,据此估计该校三年级的600名学生中,对二十四节气歌一句也说不出的有( )
A.17人B.83人C.102人D.115人
【解析】一句也说不出的学生频率为,
所以估计名学生中,一句也说不出的有人.
故选:C
8.在第个“三八”国际妇女节到来之际,我们年级组给每位女教师送了火红的玫瑰和热情洋溢的贺卡,其中我最喜欢的一句话英文翻译是:“Yu stand n the pdium as an ath and tell the rdinary as a fairly tale.”统计如下表:
累计频数为,则字母“”出现的频率约为多少?( )
A.B.C.D.
【解析】由表格数据可知:字母“”对应的频数为,字母“”出现的频率约为.
故选:B.
9.已知使用一剂某种药物治愈某种疾病的概率为90%,则下列说法正确的是( )
A.如果有100个这种病人各使用一剂这样的药物,那么有90人会被治愈;
B.如果一个患有这种疾病的病人使用两剂这样的药物就一定会被治愈;
C.使用一剂这种药物治愈这种疾病的可能性是90%;
D.以上说法都不对.
【解析】使用一剂某种药物治愈某种疾病的概率为,即使用一剂这种药物治愈这种疾病的可能性是,故C正确;
如果有100个这种病人各使用一剂这样的药物,被治愈的人数理论预测值为人,不一定必有人被治愈,故A错误;
如果一个患有这种疾病的病人使用两剂这样的药物被治愈的概率为,也可能不被治愈,故B错误;
故选:C
10.下列四个命题中正确的是( )
A.设有一批产品,其次品率为,则从中任取200件,必有10件是次品
B.做100次抛硬币的试验,结果51次出现正面,因此出现正面的概率是
C.随机事件发生的频率就是这个随机事件发生的概率
D.抛掷骰子100次,得点数是1的结果18次,则出现1点的频率是
【解析】对于A,次品率是大量产品的估计值,并不是必有10件是次品,故A错误;
对于B,抛硬币出现正面的概率是,而不是,故B错误;
对于C,频率与概率不是同一个概念,故C错误;
对于D,利用频率计算公式求得频率,故D正确.
故选:D
11.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选”提高检测效率:每16人为组,把每个人抽取的鼻咽拭子分泌物混合检查,如果为阴性则全部放行;若为阳性,则对该16人再次抽检确认感染者.某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组,继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查……以此类推,最终从这16人中认定那名感染者需要经过( )次检测.
A.3B.4C.5D.6
【解析】16人平均分成两级,经过一次检验确定感染者在其中的8人中,再平均分成两组,第二次检测,确定感染者在其中的4人中,再平均分成两组,
第三次检测,确定感染者在其中的2人中,最后第四次检测,确定感染者.共4次检测.
故选:B.
12.在这个热“晴”似火的7月,多地持续高温,某市气象局将发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温37摄氏度以上的概率是.某人用计算机生成了20组随机数,结果如下:
若用0,1,2,3,4表示高温橙色预警,用5,6,7,8,9表示非高温橙色预警,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是( )
A.B.C.D.
【解析】今后的3天中恰有2天发布高温橙色预警信号的随机数有12个,分别为:
116, 812, 730, 452, 125, 217, 109, 361, 284, 147, 318, 027,
则今后的3天中恰有2天发布高温橙色预警信号的概率估计是:,
故选:A.
13.某种心脏手术,成功率为0.6,现采用随机模拟方法估计“3例心脏手术全部成功”的概率:先利用计算器或计算机产生0~9之间取整数值的随机数,由于成功率是0.6,我们用0,1,2,3表示手术不成功,4,5,6,7,8,9表示手术成功;再以每3个随机数为一组,作为3例手术的结果,经随机模拟产生如下10组随机数:
812,832,569,683,271,989,730,537,925,907
由此估计“3例心脏手术全部成功”的概率为( )
A.0.2B.0.3C.0.4D.0.5
【解析】由题意,10组随机数:812,832,569,683,271,989,730,537,925,907,表示“3例心脏手术全部成功”的有: 569, 989,故2个,
故估计“3例心脏手术全部成功”的概率为.
故选:A.
14.抛掷一枚质地均匀的硬币,设事件“正面向上”,则下列说法正确的是( )
A.抛掷硬币10次,事件A必发生5次
B.抛掷硬币100次,事件A不可能发生50次
C.抛掷硬币1000次,事件A发生的频率一定等于0.5
D.随着抛掷硬币次数的增多,事件A发生的频率在0.5附近波动的幅度较大的可能性小
【解析】不管抛掷硬币多少次,事件A发生的次数是随机事件,故ABC错误;
随着抛掷硬币次数的增多,事件A发生的频率在0.5附近波动的幅度较大的可能性小;
故选:D
15.某车间从生产的一批产品中随机抽取了1000个零件进行一项质量指标的检测,整理检测结果得此项质量指标的频率分布直方图如图所示,则下列结论错误的是( )
A.
B.估计这批产品该项质量指标的众数为45
C.估计这批产品该项质量指标的中位数为60
D.从这批产品中随机选取1个零件,其质量指标在的概率约为0.5
【解析】,解得,故A正确;
频率最大的一组为第二组,中间值为,所以众数为45,故B正确;
质量指标大于等于60的有两组,频率之和为,所以60不是中位数,故C错误;
由于质量指标在[50,70)之间的频率之和为,可以近似认为从这批产品中随机选取1个零件,其质量指标在的概率约为0.5,故D正确.
故选:
16.某超市计划按月订购一种冷饮,根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25℃,需求量为600瓶;如果最高气温位于区间,需求量为300瓶;如果最高气温低于20℃,需求量为100瓶.为了确定6月份的订购计划,统计了前三年6月份各天的最高气温数据,得到下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.若6月份这种冷饮一天的需求量不超过x瓶的概率估计值为0.1,则x=( )
A.100B.300C.400D.600
【解析】这种冷饮一天的需求量不超过300瓶,当且仅当最高气温低于25℃,
由表格数据知,最高气温低于25℃的频率为,
所以6月份这种冷饮一天的需求量不超过300瓶的概率估计值为0.1.
故选:B.
二、多选题
17.利用计算机模拟掷两枚硬币的试验,在重复试验次数为20,100,500时各做5组试验,得到事件A=“一个正面朝上,一个反面朝上”.发生的频数和频率表如下:
根据以上信息,下面说法正确的有( )
A.试验次数相同时,频率可能不同,说明随机事件发生的频率具有随机性
B.试验次数较小时,频率波动较大;试验次数较大时,频率波动较小,所以试验次数越少越好;
C.随机事件发生的频率会随着试验次数增加而逐渐稳定在一个固定值附近
D.我们要得到某事件发生的概率时,只需要做一次随机试验,得到事件发生的频率即为概率
【解析】A选项,验次数相同时,频率可能不同,说明随机事件发生的频率具有随机性,故正确;
试验次数较小时,频率波动较大;试验次数较大时,频率波动较小,所以试验次数越多越好;B错误;
随机事件发生的频率会随着试验次数增加而逐渐稳定在一个固定值附近,此固定值就是概率,C正确;
我们要得到某事件发生的概率时,需要进行多次试验才能得到概率的估计值,故D错误.
故选:AC
18.某学校组织了一次劳动技能大赛,共有100名学生参赛,经过评判,这100名参赛者的得分都在内,得分60分以下为不及格,其得分的频率分布直方图如图所示(按得分分成这五组),则下列结论正确的是( )
A.直方图中
B.此次比赛得分不及格的共有40人
C.以频率为概率,从这100名参赛者中随机选取1人,其得分在的概率为0.5
D.这100名参赛者得分的中位数为65
【解析】因为,所以,所以A正确;
因为不及格的人数为,所以B正确;
因为得分在的频率为,所以从这100名参赛者中随机选取1人,其得分在的概率为0.5,所以C正确;
这100名参赛者得分的中位数为,所以D错误.
故选:ABC.
19.豆瓣评分是将用户评价的一到五星转化为0~10的分值(一星2分,二星4分,三星6分,以此类推),以得分总和除以评分的用户人数所得的数字.国庆爱国影片《长津湖》的豆瓣评分情况如图,假如参与评价的观众中有97.6%的评价不低于二星,则下列说法正确的是( )
A.m的值是32%
B.随机抽取100名观众,则一定有24人评价五星
C.随机抽取一名观众,其评价是三星或五星的概率约为0.56
D.若从已作评价的观众中随机抽取3人,则事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件
【解析】对A选项,参与评价的观众中有97.6%的评价不低于二星,
则,所以,故A正确;
对B选项,随机抽取100名观众,可能有人评价五星,但不是一定的,故B错误;
对C选项,由A选项,评价是三星或五星的概率约为,故C正确;
对D选项,根据互斥事件和对立事件的定义可知,事件“至多1人评价五星”与事件“恰有2人评价五星”是互斥且不对立事件,故D正确;
故选:ACD
20.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品,若用C表示抽到次品这一事件.则下列说法中不正确的是( )
A.事件C发生的概率为B.事件C发生的频率为
C.事件C发生的概率接近D.每抽10台电视机,必有1台次品
【解析】事件C发生的频率为,由于只做了一次实验,故不能得到概率为或概率接近;
当然每抽10台电视机,必有1台次品也不一定发生.
故B正确,ACD错误.
故选:ACD
三、填空题
21.从一堆苹果中任取10只,称得它们的质量(单位:g)如下.
125 120 122 105 130 114 116 95 120 134
则样本数据落在内的频率为______.
【解析】因为样本数据落在内的有4个:120,122,116,120,
所以样本数据落在内的频率为,
故答案为:0.4.
22.从存放号码分别为1,2,3,…,10的卡片的盒子里,有放回地取100次,每次取一张卡片,并记下号码,统计结果如下:
取到号码为奇数的频率为______.
【解析】由数表知,取到奇数号码的次数是:,
所以取到号码为奇数的频率为.
故答案为:0.58
23.在某一时期内,一条河流某处的年最高水位在各个范围内的频率如下表:
若当最高水位低于14米时为“安全水位”,则出现“安全水位”的频率是__________.
【解析】由表格得:出现“安全水位”的频率是
故答案为:0.76
24.某超市计划按月订购一种冷饮,根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25℃,需求量为600瓶;如果最高气温位于区间 ,需求量为300瓶;如果最高气温低于20℃,需求量为100瓶.为了确定6月份的订购计划,统计了前三年6月份各天的最高气温数据,得到下面的频数分布表:
以最高气温位于各区间的频率估计最高气温位于该区间的概率.若6月份这种冷饮一天的需求量不超过瓶的概率估计值为0.1,则___________.
【解析】由表可知,最高气温低于的频率为:,
所以月份这种冷饮一天的需求量不超过瓶的概率估计值为.
故答案为:.
25.关于频率和概率,下列说法中正确的是______.(填序号)
①某同学在罚球线投篮三次,命中两次,则该同学每次投篮的命中率为;
②数学家皮尔逊曾经做过两次试验,抛掷12000次硬币,得到正面向上的频率为0.5016;抛掷24000次硬币,得到正面向上的频率为0.5005.如果他抛掷36000次硬币,正面向上的频率可能大于0.5005;
③某类种子发芽的概率为0.903,当我们抽取2000粒种子试种,一定会有1806粒种子发芽;
④将一颗均匀的骰子抛掷6000次,则出现点数大于2的次数大约为4000次.
【解析】①某同学投篮三次,命中两次,只能说明在这次投篮中命中的频率为,不能说概率,故错误;
②进行大量的实验,硬币正面向上的频率在0.5附近摆动,可能大于0.5,也可能小于0.5,故正确;
③只能说明可能有1806粒种子发芽,具有随机性,并不是一定有1806粒种子发芽,故错误;
④出现点数大于2的次数大约为4000次,故正确.
故答案为:②④
26.目前,北京医疗机构日常核酸检测主要分为合样本混检和单样本检测.合样本混检是指:先将个人的样本混合在一起进行次检测,如果这个人都没有感染新冠病毒,则检测结果为阴性,得到每人的检测结果都为阴性,检测结束;如果这个人中有人感染新冠病毒,则检测结果为阳性,此时需对每人再进行次单独检测,得到每人的检测结果,检测结束.某社区有人,若新冠病毒的感染率为,为了获得社区每个人的核酸检测结果,可以选择对所有人都进行单样本检测,也可以选择对所有人都进行合样本混检.已知合样本混检时每个样本检测费用为元,单样本检测时每个样本检测费用为元.当_____时,选择单样本检测总费用更低.(写出一个符合条件的集合即可)
【解析】若选择单样本检测,则检测总费用为:元;
若采用合样本混检,可将社区人员分为组,
新冠病毒的感染率为,有组感染新冠病毒,
此时检测总费用为:元;
令,解得:,
当时,选择单样本检测的总费用更低.
故答案为:.
四、解答题
27.甲乙两名选手在“10米气步枪”训练赛上的成绩(环数)如茎叶图所示.
(1)成绩不低于590环即可通过预选赛进入初赛,估计甲乙两位选手在“10米气步枪”比赛中成绩不低于590环的可能性,据此估计哪位选手更有可能通过预选赛;
(2)按往年记录,成绩不低于594环即有大概率进入决赛,估计甲乙两位选手在“10米气步枪”比赛中成绩不低于594环的可能性,据此估计哪位选手更有可能进入决赛.
【解析】(1)甲选手在“10米气步枪”比赛中成绩不低于590环的可能性为,
乙选手在“10米气步枪”比赛中成绩不低于590环的可能性为,
,所以,乙选手更有可能通过预选赛.
(2)甲选手在“10米气步枪”比赛中成绩不低于594环的可能性为,
乙选手在“10米气步枪”比赛中成绩不低于594环的可能性为,
,所以,甲选手更有可能进入决赛.
28.受精的新鲜鸡蛋在适宜的温度下平均需要21天孵化出小鸡,对于1个鸡蛋来说,它可能20天孵出,也可能21天孵出,……,下表是不同孵化天数的鸡蛋数的记录:
(1)求孵化天数在21天的经验概率;
(2)求孵化天数超过21天的频率.
【解析】(1)由表格数据可以得到:一共有个鸡蛋,其中在21天孵化的鸡蛋数为820个,故孵化天数在21天的经验概率就是频率,故答案为;
(2)孵化天数超过21天的鸡蛋个数为,故孵化天数超过21天的频率为.
29.为了研究某种油菜籽的发芽率,科研人员在相同条件下做了8批试验,油菜籽发芽试验的相关数据如下表.
(1)如何计算各批试验中油菜籽发芽的频率?
(2)由各批油菜籽发芽的频率,可以得到频率具有怎样的特征?
(3)如何确定该油菜籽发芽的概率?
【解析】(1)利用公式:频率,可求出各批试验中油菜籽发芽的频率.
(2),,,,,,,,
当试验次数越来越多时,频率越来越趋近于一个常数.
(3)由(2)可知,当试验次数越来越多时,频率在0.900附近波动,由此可估计该油菜籽发芽的概率约为0.900.
30.某企业为了检测甲、乙两条生产线上零件的质量情况,现从甲、乙两条生产线上各抽取20个零件作为样本,检测一项质量指标值(质量指标值越高,产品质量越好),得到下表.
(1)将产品质量指标值分成三个等级:
假设甲、乙两条生产线相互独立,根据所给数据,以事件发生的频率作为相应事件发生的概率,分别求甲、乙两条生产线生产的零件为一等品的概率;
(2)分别计算两组数据的平均数,从计算结果来看,哪条生产线上的产品质量好?
【解析】(1)甲生产线零件一等品的概率为,乙生产线零件一等品的概率为.
(2),
,
因为,甲生产线上的产品质量好.
9533
9522
0018
7472
0018
3879
5869
3281
7890
2692
8280
8425
3990
8460
7980
2436
5987
3882
0753
8935
网站①评价人数
网站①好评率
网站②评价人数
网站②好评率
餐馆甲
1000
95%
1000
85%
餐馆乙
1000
100%
2000
80%
餐馆丙
1000
90%
1000
90%
餐馆丁
2000
95%
1000
85%
字母
y
u
s
a
p
d
e
t
f
l
i
n
m
r
h
频数
3
5
2
3
10
1
4
4
6
1
4
3
5
1
3
3
116
785
812
730
134
452
125
689
024
169
334
217
109
361
908
284
044
147
318
027
最高气温
天数
4
5
25
38
18
序号
频数
频率
频数
频率
频数
频率
1
12
0.6
56
0.56
261
0.522
2
9
0.45
50
0.55
241
0.482
3
13
0.65
48
0.48
250
0.5
4
7
0.35
55
0.55
258
0.516
5
12
0.6
52
0.52
253
0.506
卡片号码
1
2
3
4
5
6
7
8
9
10
取到次数
17
8
5
7
6
9
18
9
12
9
最高水位范围(米)
<10
[14,16)
≥16
频率
0.1
0.28
0.38
0.16
0.08
最高气温
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
天数
4
5
25
38
18
孵化天数
20
21
22
23
鸡蛋数
0
49
820
93
38
0
批次
1
2
3
4
5
6
7
8
每批粒数
5
10
130
700
1500
2000
3000
5000
发芽粒数
4
9
116
637
1370
1786
2709
4490
甲
67
78
83
92
95
85
79
68
58
94
81
86
95
87
97
93
88
81
82
91
乙
73
83
82
54
91
76
83
75
68
82
93
95
92
81
84
66
89
87
65
91
质量指标值
低于60
60到80
不低于80
产品等级
不合格品
二等品
一等品
高中10.3 频率与概率精品精练: 这是一份高中10.3 频率与概率精品精练,文件包含第06讲频率与概率-高一数学下学期考点精讲+精练人教A版2019必修第二册解析版docx、第06讲频率与概率-高一数学下学期考点精讲+精练人教A版2019必修第二册原卷版docx等2份试卷配套教学资源,其中试卷共40页, 欢迎下载使用。
人教A版 (2019)必修 第二册10.1 随机事件与概率优秀课时练习: 这是一份人教A版 (2019)必修 第二册10.1 随机事件与概率优秀课时练习,文件包含第01练随机抽样-高一数学下学期考点精讲+精练人教A版2019必修第二册解析版docx、第01练随机抽样-高一数学下学期考点精讲+精练人教A版2019必修第二册原卷版docx等2份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
高中数学8.6 空间直线、平面的垂直精品达标测试: 这是一份高中数学8.6 空间直线、平面的垂直精品达标测试,文件包含第06讲空间直线平面的垂直-高一数学下学期考点精讲+精练人教A版2019必修第二册解析版docx、第06讲空间直线平面的垂直-高一数学下学期考点精讲+精练人教A版2019必修第二册原卷版docx等2份试卷配套教学资源,其中试卷共58页, 欢迎下载使用。













