苏科版八年级下册11.1 反比例函数课后练习题

班级              姓名             学号             分数           

第10章  反比例函数（A卷·知识通关练）

核心知识1. 反比例函数的定义

1．用函数表达式表示下列问题中的两个变量之间的关系，其中是反比例函数的关系是 　    　．

（1）长为100m的绳子剪下m米后，还剩下n米；

（2）买单价为10元的笔记本x本，一共用了y元；

（3）矩形的面积为24cm2，相邻两边的边长是xcm、ycm；

（4）家到学校的距离为480米，步行上学平均速度v米/分钟，所用时间为t分钟；

2．下列函数，①x（y+2）＝1②y③y④y⑤y⑥y；其中是y关于x的反比例函数的有：　      　．

3．若函数是反比例函数，则m的值是 　　．

4．已知函数y是y关于x的反比例函数，则m＝　    　．

5．若函数y是关于x的反比例函数，则a满足的条件是 　     　．

6．将x代入反比例函数y中，所得函数值记为y1，又将x＝y1+1代入原反比例函数中，所得函数值记为y2，再将x＝y2+1代入原反比例函数中，所得函数值记为y3，…，如此继续下去，则y2015＝　　．

核心知识2. 反比例函数的图像

1．函数y的图象的两个分支分布在第　   　象限．

2．如果反比例函数的图象经过点（﹣3，﹣4），那么函数的图象在第　   　象限．

3．已知反比例函数的图象如图，则m的取值范围是　   　．

4．函数的图象如图所示，下列对该函数性质的论断正确的是　   　

（1）该函数的图象是中心对称图形；

（2）当x＞0时，该函数在x＝1时取得最小值2；

（3）在每个象限内，y的值随x值的增大而减小；

（4）y的值不可能为1．

5．如图，符合图象的解析式是　   　．（填序号）

①y②y③y和y④y．

核心知识3. 反比例函数的性质

1．已知反比例函数的图象位于第二、四象限，则k的取值范围是 　   　．

2．已知反比例函数y的图象的每支都是y随x的增大而增大，则a的取值范围为 　   　．

3．若反比例函数的图象位于第一、三象限，则k的值是 　   　．

4．使关于x的分式方程2的解为非负数，且使反比例函数y图象过第一、三象限时满足条件的所有整数k的和为　   　．

5．若点A（﹣1，y1）、B（，y2）、C（1，y3）都在反比例函数y（k为常数）的图象上，则y1、y2、y3的大小关系为 　   　．

6．当1≤x≤2时，反比例函数y（k＞﹣3且k≠0）的最大值与最小值之差是1，则k的值是　   　．

7．已知反比例函数y，下列结论：①图象必经过点（﹣1，2）；②y随x的增大而增大；③图象在第二、四象限内；④若x＞1，则y＞﹣2．其中正确的有　   　．（填序号）

核心知识4. 反比例函数k值的几何意义

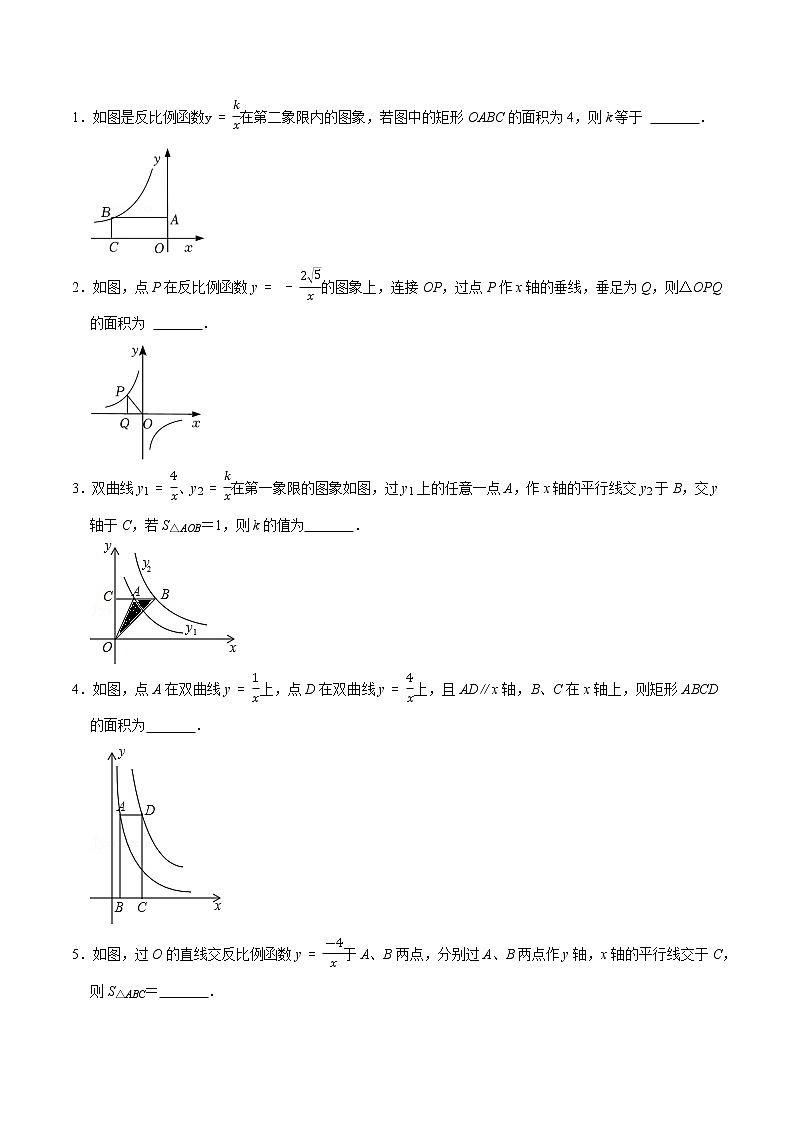
1．如图是反比例函数在第二象限内的图象，若图中的矩形OABC的面积为4，则k等于 　   　．

2．如图，点P在反比例函数y的图象上，连接OP，过点P作x轴的垂线，垂足为Q，则△OPQ的面积为 　   　．

3．双曲线y1、y2在第一象限的图象如图，过y1上的任意一点A，作x轴的平行线交y2于B，交y轴于C，若S△AOB＝1，则k的值为　   　．

4．如图，点A在双曲线y上，点D在双曲线y上，且AD∥x轴，B、C在x轴上，则矩形ABCD的面积为　   　．

5．如图，过O的直线交反比例函数y于A、B两点，分别过A、B两点作y轴，x轴的平行线交于C，则S△ABC＝　   　．

6．如图，A、B两点在双曲线y上，分别经过A、B两点向坐标轴作垂线段，已知S阴影＝1，则S1+S2＝　   　．

7．如图，在平面直角坐标系中，点A是x轴上任意一点，BC∥x轴，分别交y（x＞0），y（x＜0）的图象于B，C两点，若△ABC的面积是3，则k的值为 　   　．

8．函数y（x＞0）与y（x＞0）的图象如图所示，点C是y轴上的任意一点．直线AB平行于y轴，分别与两个函数图象交于点A、B，连结AC、BC．当AB从左向右平移时，△ABC的面积是 　   　．

9．如图，函数y（x＞0）和（x＞0）的图象分别是l1和l2．设点P在l2上，PA∥y轴交l1于点A，PB∥x轴交l1于点B，△PAB的面积为 　   　．

10．如图，反比例函数y的图象上有两点A（2，4）、B（4，b），则△AOB的面积为　   　．

核心知识5. 待定系数法求反比例函数解析式

1．一个反比例函数图象过点A（2，3），则这个反比例函数的解析式是 　   　．

2．已知点P位于第三象限内，且点P到两坐标轴的距离分别为3和2．若反比例函数图象经过点P，则该反比例函数的解析式为 　   　．

3．如图，正方形ABOC的边长为2，反比例函数过点A，则反比例函数的解析式为：　   　．

4．已知y与x﹣3成反比例，当x＝4时，y＝﹣1；那么当x＝﹣4时，y＝　   　．

5．如图，四边形ABCD是平行四边形，点A（1，0），B（3，1），C（3，3）．反比例函数的图象经过点D，则反比例函数的解析式是 　   　．

6．如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，﹣3），反比例函数y（k≠0）的图象经过点C．

（1）点D的坐标为 　   　；

（2）求反比例函数的解析式．

7．已知y与2x﹣3成反比例，且当x＝2时，y＝4，求y关于x的函数解析式．

核心知识6. 设点坐标解决反比例函数问题

1．如图，A、B为反比例函数图象上两点，过A作AE⊥x轴于点E，过B作BC⊥x轴于点C，BD⊥y轴于点D，AE、BD交于点F，连接AB，若S△ABF＝2，BC：AE＝1：3，则k＝　   　．

2．如图，点A、B在反比例函数的图象上，过点A、B作x轴的垂线，垂足分别是M、N，射线AB交x轴于点C，若OM＝MN＝NC，四边形AMNB的面积是4，则k的值为 　   　．

3．如图，两个反比例函数y和y在第一象限内的图象依次是C1和C2，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，若四边形PAOB的面积为5，则k＝　   　．

4．如图，正方形ABCD的顶点分别在反比例函数y（k1＞0）和y（k2＞0）的图象上，若BD∥y轴，点D的横坐标为4，则k1+k2＝　   　．

5．如图，点A在双曲线上，点B在双曲线上，AB∥y轴，BC⊥y轴，垂足为点C，连接AC，若△ABC的面积是4，则k的值为 　   　．

6．如图，△AOB的边OB在x轴上，且∠ABO＝90°，反比例函数y（x＞0）的图象与边AO、AB分别相交于点 C、D，连接BC，已知OC＝BC，△BOC的面积为12，若AD＝6，直线OA的函数解析式为 　   　．

7．如图，点A、B在反比例函数的图象上，连接OB、AB，以OB、AB为边作平行四边形ABOC．若点C恰好落在反比例函数的图象上，则SABOC＝　   　．

8．如图，两个边长分别为a，b（a＞b）的正方形连在一起，三点C，B，F在同一直线上，反比例函数y在第一象限的图象经过小正方形右下顶点E．若OB2﹣BE2＝8，则k的值是 　   　．

核心知识7 反比例函数与一次函数的综合题

1．如图，一次函数y1＝kx+b（k≠0）的图象与反比例函数y2（m为常数且m≠0）图象的都经过A（﹣1，2），B（2，﹣1），结合图象，则方程kxb的解是 　   　，不等式kxb的解集是 　   　．

2．如图，一次函数y1＝k1x+b1的图象与反比例函数y2的图象相交于点A（5，m），B（﹣1，n）两点，当y1＞y2时，则自变量x的取值范围是 　   　．

3．如图，在平面直角坐标系中，函数y＝kx+b（k≠0）与y（m≠0）的图象相交于点A（2，3），B（﹣6，﹣1），则关于x的不等式kx+b的解集是　   　．

4．如图，在平面直角坐标系中，直线yx与反比例函数（x＜0）的图象交于点A（﹣2，m），将直线yx沿y轴向上平移b个单位长度，交y轴于点B，交反比例函数图象于点C，连接OC，若OA＝2BC，则b的值为 　   　．

5．如图，直线y＝﹣x+m（m＞0）与双曲线y（x＞0）交于A、B两点，连接OA、OB，AM⊥y轴于M，BN⊥x轴于N，设OA，OB的解析式分别为y＝ax，y＝bx，现有以下结论：①m＞2；②AM+BN＝AB；③若∠AOB＝45°，则S△AOB＝1；④a+b有最小值．其中正确的是 　   　．（写出所有正确结论的序号）

6．如图，在平面直角坐标系xOy中，直线AB与x轴、y轴分别交于点A，B，与反比例函数（k为常数，且k＞0）在第一象限的图象交于点E，F．过点E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C．若．记△CEF的面积为S1，△OEF的面积为S2，则　   　．

核心知识8. 反比例函数的实际应用

1．已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．

（1）求这个反比例函数的解析式，并直接写出蓄电池的电压值（单位：v）

（2）如果以此蓄电池为电源的用电器的限制电流不能超过10A，那么用电器可变电阻应控制在什么范围？

2．小明设计了杠杆平衡实验：如图，取一根长70cm质地均匀的木杆，用细绳绑在木杆的中点O处并将其吊起来，在左侧距离中点O20cm处挂一个重9N的物体，为了保持木杆水平（动力×动力臂＝阻力×阻力臂），在中点O右侧用一个弹簧测力计竖直向下拉，改变弹簧测力计与中点O的距离L（单位：cm），看弹簧测力计的示数F（单位：N）有什么变化，小明在做此活动时，得到下表的数据．

（1）表中第 　   　组数据是明显错误的；

（2）在已学过的函数中选择合适的模型，求F关于L的函数解析式；

（3）若弹簧测力计的最大量程是10N，求L的取值范围．

3．为防控疫情，学校对学生宿舍进行消毒工作．先经过5min的集中药物喷洒，再封闭宿舍10min，然后打开门窗进行通风，宿舍内空气中含药量y（mg/m3）与时间x（min）之间的函数图象如图所示，打开门窗前为线段OA和线段AB，打开门窗后为反比例函数关系．

（1）求线段OA和反比例函数的表达式；

（2）当室内空气中的含药量不低于4mg/m3且持续时间不低于30分钟时，才能有效消毒，请问这次消毒工作是否有效？

4．某标准游泳池的尺寸为长50米，宽25米，深3米，游泳池蓄水能游泳时，水深不低于1.8米．

（1）该游泳池能游泳时，最低蓄水量是多少立方米？

（2）游泳池的排水管每小时排水x立方米，那么将游泳池最低蓄水量排完用了y小时．

①写出y与x的函数关系式；

②当x＝225时，求y的值；

③如果增加排水管，使每小时排水量达到s立方米，则时间y会 　   　（选填“增大”或“减小”）．

④在②的情况下，如果最低蓄水量排完不超过5小时，每小时排水量最少增加多少立方米？