专题2-3 函数性质3：幂指对函数图像与零点-高考数学一轮复习热点题型归纳与变式演练（全国通用）

这是一份专题2-3 函数性质3：幂指对函数图像与零点-高考数学一轮复习热点题型归纳与变式演练（全国通用），文件包含专题2-3函数性质3幂指对函数图像与零点-高考数学一轮复习热点题型归纳与变式演练全国通用解析版docx、专题2-3函数性质3幂指对函数图像与零点-高考数学一轮复习热点题型归纳与变式演练全国通用原卷版docx等2份试卷配套教学资源，其中试卷共57页， 欢迎下载使用。
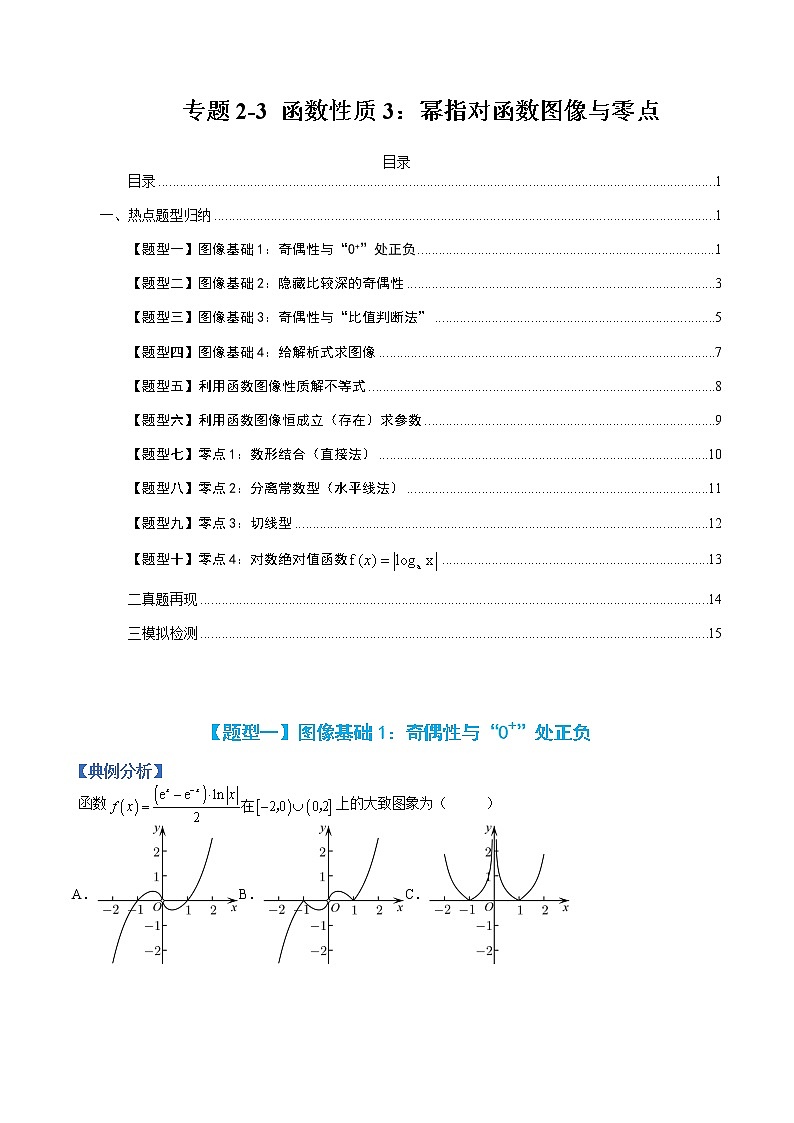
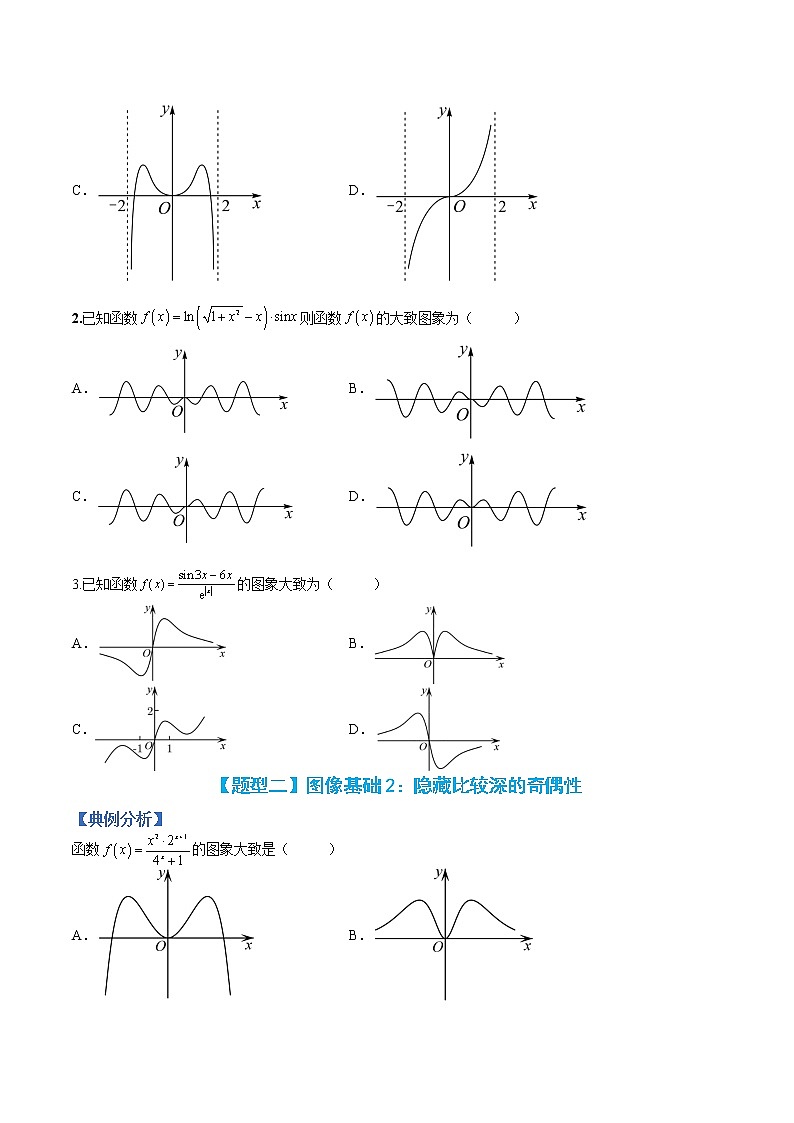
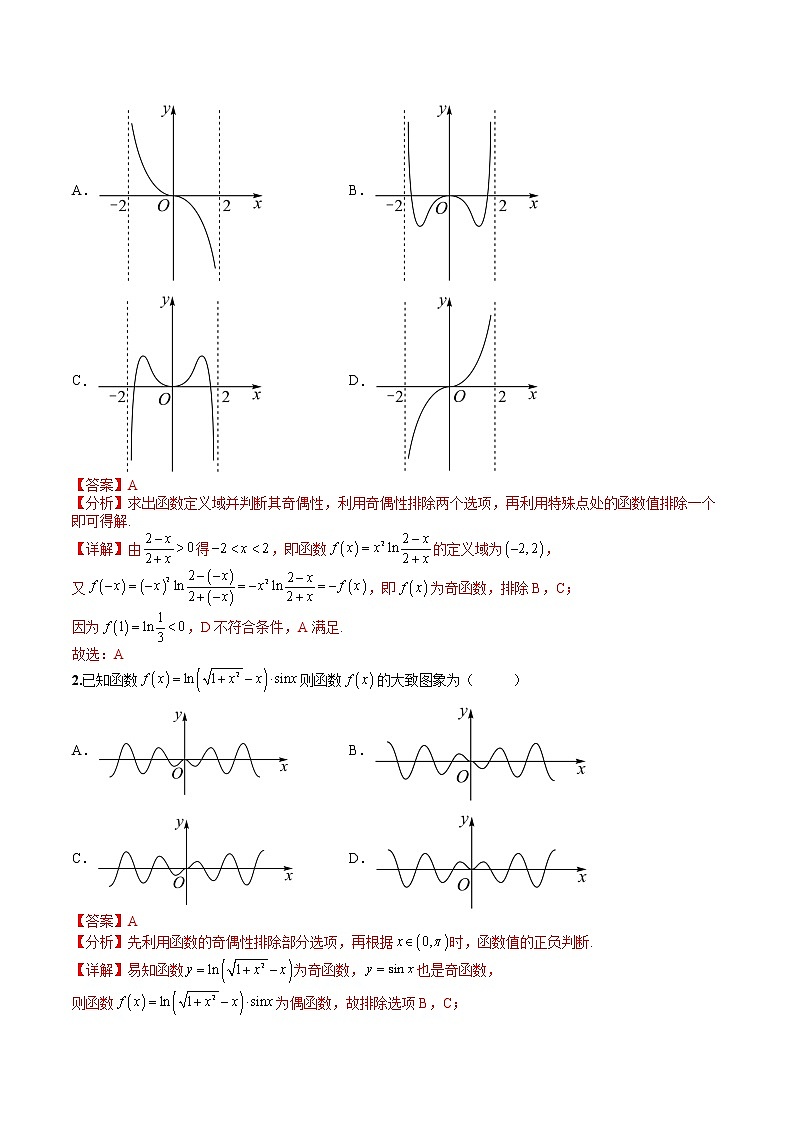
专题2-3 函数性质3：幂指对函数图像与零点 目录目录一、热点题型归纳【题型一】图像基础1：奇偶性与“0+”处正负【题型二】图像基础2：隐藏比较深的奇偶性【题型三】图像基础3：奇偶性与“比值判断法”【题型四】图像基础4：给解析式求图像【题型五】利用函数图像性质解不等式【题型六】利用函数图像恒成立（存在）求参数【题型七】零点1：数形结合（直接法）【题型八】零点2：分离常数型（水平线法）【题型九】零点3：切线型【题型十】零点4：对数绝对值函数二真题再现三模拟检测  【题型一】图像基础1：奇偶性与“0+”处正负【典例分析】 函数上的大致图象为（       ）A．B．C．D．  【提分秘籍】基本规律作为函数基础之一的“识图”题型，多做此类训练题，有助于学生对函数图像熟练掌握，进而增加对函数图像及其之间的变化有深刻的认识。此类题尽量避开运算量大的求导，如有肯能，也可以避开一些复杂的“代特殊值计算”。可以从下边几个方向来判断。一、.奇偶性判断，要注意积累常见的奇函数、偶函数。二、0的极限处正负判断，一般多从.处判断。【变式演练】1.函数的大致图象是（       ）A． B．C． D． 2.已知函数则函数的大致图象为（       ）A． B．C． D． 3.已知函数的图象大致为（       ）A． B．C． D．【题型二】图像基础2：隐藏比较深的奇偶性【典例分析】函数的图象大致是（       ）A． B．C． D． 【提分秘籍】基本规律隐藏较深的奇偶函数2.一些变形后的奇（偶）函数如，，  【变式演练】1.函数图象的大致形状为（       ）A． B．C． D． 2.函数的部分图象大致为（       ）A． B．C． D． 3.函数的图像大致为(   )A． B． C．  D．  【题型三】图像基础3：奇偶性与“比值判断法”【典例分析】的图像大致是（  ）A． B． C． D．   【提分秘籍】基本规律“比值判断法”，如下图，在，可知图像“大小” 【变式演练】1.函数的大致图象是（       ）A． B．C． D． 2.函数的大致图象是（       ）A． B．C． D．3.函数的图像大致为（    ）A． B．C． D．    【题型四】图像基础4：给解析式求图像【典例分析】已知某个函数的图像如图所示，则下列解析式中与此图像最为符合的是（       ）A． B．C． D．   【提分秘籍】基本规律此类题型虽然较难，但可以从代特殊值入手。 【变式演练】1.已知函数的图象如图所示，则的解析式可能是（       ）A．（） B．（）C．（） D．（） 2.已知函数f(x)的图像如图所示，则函数f(x)的解析式可能是（       ）A． B．C． D． 3.已知函数的部分图像如图所示，则该函数的解析式可能是（       ） A． B．C． D．     【题型五】利用函数图像性质解不等式【典例分析】若关于x的不等式有实数解，则实数a的取值范围是（       ）A． B． C． D． 【提分秘籍】基本规律1.幂指对等函数图像之间的位置关系。2.幂指对等函数的性质及其应用  【变式演练】1.设函数则满足的的取值范围是（       ）A． B． C． D． 2.若，其中且，则实数的取值范围是（       ）A． B．C． D． 3.已知是定义在上的偶函数，在区间上单调递增，且函数.若实数满足，则实数的取值范围是（       ）A． B． C． D．【题型六】利用函数图像恒成立（存在）求参数【典例分析】已知，在上恒成立，则实数的取值范围为（       ）A． B． C． D．     【提分秘籍】基本规律不等式恒成立（存在）问题常见方法：①分离参数恒成立(即可)或恒成立（即可）；②数形结合( 图像在 上方即可)；③讨论最值或恒成立.  【变式演练】1.已知幂函数在上单调递增，函数时，总存在使得，则的取值范围是（ ）A． B． C． D． 2.已知，若函数有最小值，则实数的取值范围是（       ）A． B． C． D． 3.已知函数，当时，不等恒成立，则实数m的取值范围是（       ）A． B． C． D．  【题型七】零点1：数形结合（直接法）【典例分析】已知函数是定义在上的偶函数，且，当时，，设函数，则的零点的个数为（       ）A．6 B．7 C．8 D．9   【提分秘籍】基本规律1.直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围2.数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解. 【变式演练】1.已知函数，则方程的实根个数为（       ）个．A．1 B．2 C．3 D．4 2.已知定义在上的函数，当时，不等式恒成立，则实数的取值范围是A． B． C． D． 3.定义在R上的偶函数满足对任意，有，且当时，，若函数在上至少有3个零点，则实数的取值范围是（       ）A． B． C． D．  【题型八】零点2：分离常数型（水平线法）【典例分析】已知函数，若函数存在四个不同的零点，则实数的取值范围是_______.  【提分秘籍】基本规律分离参数法：先将参数分离，转化成求函数的值域问题加以解决； 【变式演练】1.已知函数，若有三个不同的实数，使得，则的取值范围为（       ）A． B．C． D． 2.已知函数，，且，则的最小值是（       ）A． B． C． D．3.定义在上的奇函数，当时，，则关于的函数的所有零点之和为（        ）A． B．C． D．  【题型九】零点3：切线型【典例分析】若函数，函数有两个零点，则的值是A．0或 B． C．0 D．   【提分秘籍】基本规律先对解析式变形，进而构造两个函数（其中一个是直线），然后在同一平面直角坐标系中画出函数与直线的图象，根据函数与直线的位置关系，借助于直线临界值处（切线）.来研究。  【变式演练】1.已知且，函数在上是单调函数，若关于的方程恰有2个互异的实数解，则的取值范围是（       ）A． B．C． D．  2.已知定义在R上的奇函数满足，已知当时，，若恰有六个不相等的零点，则实数m的取值范围为（       ）A． B．C． D． 3.函数（），若的解集为，且中只有一个整数，则实数的取值范围为A． B．C． D．     【题型十】零点4：对数绝对值函数【典例分析】已知函数，其中，若的四个零点从小到大依次为，，，，则的值是（       ）A．13 B．12 C．10 D．6   【提分秘籍】基本规律对于，若有两个零点，则满足1.2.3.要注意上述结论在对称轴作用下的“变与不变”  【变式演练】1.已知函数，若存在实数，当时，满足，则的取值范围是（       ）A． B．[ C． D．  2.已知函数，函数有四个不同的零点，且满足：，     则的取值范围是（     ）A． B． C． D．3.已知函数，若存在实数，，，满足 ，且，则的取值范围是A． B． C． D．   1.如图，函数的图象为折线，则不等式的解集是A． B．C． D． 2．设函数，则f(x)（       ）A．是偶函数，且在单调递增 B．是奇函数，且在单调递减C．是偶函数，且在单调递增 D．是奇函数，且在单调递减  3．已知函数与图象上存在关于轴对称的点，则的取值范围是A． B． C． D． 4．下列函数中，既是偶函数，又是在区间上单调递减的函数为（ ）A． B． C． D． 5．已知函数的图象如图所示，则满足的关系是（     ）A． B．C． D． 6．已知两条直线：y=m和： y=(m＞0)，与函数的图像从左至右相交于点A，B ，与函数的图像从左至右相交于C,D .记线段AC和BD在X轴上的投影长度分别为a ,b ,当m 变化时，的最小值为A． B． C． D． 7．青少年视力是社会普遍关注的问题，视力情况可借助视力表测量．通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记录表的数据V的满足．已知某同学视力的五分记录法的数据为4.9，则其视力的小数记录法的数据为（       ）（）A．1.5 B．1.2 C．0.8 D．0.6 8．设函数，若的图象与图象有且仅有两个不同的公共点,则下列判断正确的是A．当时，B．当时，C．当时，D．当时，   1.函数的部分图像大致为（       ）A． B．C． D． 2.函数的大致图像为（   ）A． B．C． D． 3.函数的图像大致为( )A． B． C． D． 4.函数的图像如图所示, 则其解析式可能是（       ）A． B．C． D． 5.已知，是方程的两个解，则A． B． C． D．  6.已知函数，满足对任意的实数，都有成立，则实数的取值范围为（       ）A． B． C． D． 7.已知函数，若对任意的，都存在唯一的，满足，则实数a的取值范围为______________.  8.已知函数至多有2个不同的零点，则实数a的最大值为（       ）．A．0 B．1 C．2 D．e9.若在内恒成立，则实数a的取值范围是（       ）A． B． C． D． 10.若不等式恒成立，则实数的范围是（       ）A． B． C． D．. 11.已知函数定义在上，当时，，若，则不等式的解集为（       ）A． B． C． D． 12.已知满足，其中e是自然对数的底数，则的值为（       ）A．e B． C． D． 13.已知，，且，则，的值不可能是（       ）A． B． C． D．  14.设，若存在正实数x，使得不等式成立，则的最大值为 （       ）A． B． C． D．  15.已知，在上恒成立，则实数的取值范围为（       ）A． B． C． D．