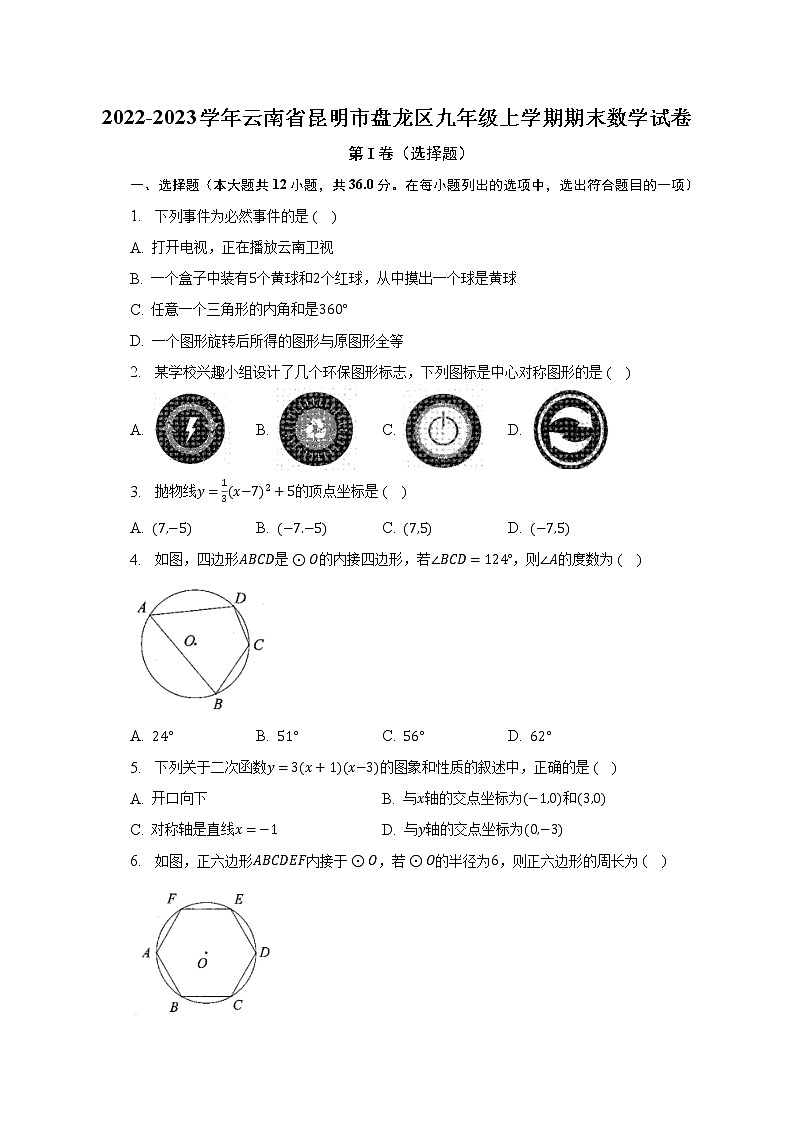
2022-2023学年云南省昆明市盘龙区九年级上学期期末数学试卷（含解析）

这是一份2022-2023学年云南省昆明市盘龙区九年级上学期期末数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列事件为必然事件的是( )
A. 打开电视，正在播放云南卫视
B. 一个盒子中装有5个黄球和2个红球，从中摸出一个球是黄球
C. 任意一个三角形的内角和是360°
D. 一个图形旋转后所得的图形与原图形全等
2. 某学校兴趣小组设计了几个环保图形标志，下列图标是中心对称图形的是( )
A. B. C. D.
3. 抛物线y=13(x−7)2+5的顶点坐标是( )
A. (7,−5)B. (−7.−5)C. (7,5)D. (−7,5)
4. 如图，四边形ABCD是⊙O的内接四边形，若∠BCD=124°，则∠A的度数为( )
A. 24°B. 51°C. 56°D. 62°
5. 下列关于二次函数y=3(x+1)(x−3)的图象和性质的叙述中，正确的是( )
A. 开口向下B. 与x轴的交点坐标为(−1,0)和(3,0)
C. 对称轴是直线x=−1D. 与y轴的交点坐标为(0,−3)
6. 如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为6，则正六边形的周长为( )
A. 36B. 18C. 63D. 32
7. 若关于x的一元二次方程x2−2x−k=0有两个不相等的实数根，则k的取值范围是( )
A. k>−1B. k<−1C. k>−1 且k≠0D. k<−1且k≠0
8. 二次函数y=x2的图象平移或翻折后经过点2,0，则下列4种方法中错误的是( )
A. 向右平移2个单位长度
B. 向右平移1个单位长度，再向下平移2个单位长度
C. 向下平移4个单位长度
D. 沿x轴翻折，再向上平移4个单位长度
9. 如图所示，圆锥形烟囱帽的底面半径为12cm，侧面展开图是圆心角为180°的扇形，则它的母线长为( )
A. 24cmB. 12cmC. 10cmD. 6cm
10. 某商场销售一批衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，商场采取了降价措施，假设在一定范围内，衬衫的单价每降1元，商场平均每天可多售出2件．如果降价后商场销售这批衬衫每天盈利1250元，衬衫的单价降了x元，那么下面所列的方程正确的是( )
A. (40−2x)(20+x)=1250B. (40−x)(20+2x)=1250
C. (40−2x)(20+2x)=1250D. (40−x)(20+x)=1250
11. 如图，在△ABC中，∠ACB=90°，将△ABC绕点C顺时针旋转得到△EDC，使点B 的对应点D恰好落在AB边上，AC、ED交于点F.若∠BCD=70°，则∠EFC的度数是( )
A. 55°B. 75°C. 105°D. 125°
12. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示，其对称轴为直线x=−12，且与x轴的一个交点坐标为−2,0.下列结论：
①abc>0； ②a=b；③9a−3b+c>0；④2a+c=0；
⑤关于x的一元二次方程ax2+bx+c=0有两个相等的实数根．
其中正确结论的个数是( )
A. 1个B. 2个C. 3个D. 4个
第II卷（非选择题）
二、填空题（本大题共4小题，共12.0分）
13. 点A(5,−1)关于原点的对称点为点B，则点B的坐标为 ．
14. “头盔是生命之盔”，质检部门对某工厂生产的头盔质量进行抽查，抽查结果如表：
估计从这批头盔中，任意抽取的一个头盔是合格产品的概率是 .(精确到0.01)
15. 若x1，x2是方程x2+3x−4=0的两个实数根，则x1+x2−x1x2的值为 ．
16. 已知⊙O的直径CD=10，AB是⊙O的弦，AB⊥CD，垂足为M，OM:OC=3:5，则AC的长为 ．
三、计算题（本大题共1小题，共6.0分）
17. 解方程：
(1)x2−4x−3=0； (2)3x(x−2)−(x−2)=0．
四、解答题（本大题共7小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）
18. (本小题8.0分)
如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标−5,2，请解答下列问题：
(1)画出△ABC关于原点对称的△A1B1C1，并写出点B1 的坐标；
(2)画出△ABC绕原点O顺时针旋转90°后得到的△A2B2C2，并写出点C2的坐标．
19. (本小题8.0分)
2022年8月8日−20日，云南省第十六届运动会在玉溪市举行，为全面发挥省运会在我省体育事业发展中的引领和示范作用，本届省运会进行了多项改革创新．其中大众组与上届相比，保留轮滑和棋牌项目，新增了工间操和射弩等项目．某体育兴趣小组收集到了工间操、射弩、轮滑、棋牌四个比赛项目规则的相关知识，并制成编号为A、B、C、D的4张卡片(如图，除编号和内容外，卡片无其他差异)，并将它们背面朝上洗匀后放在桌子上．
A：工间操
B：射弩
C：轮滑
D：棋牌
(1)从中随机抽取一张，抽到“射弩”的概率为______；
(2)若甲同学从4张卡片中随机抽取1张不放回，乙同学再从余下的3张卡片中随机抽取1张，然后根据抽取的卡片讲述卡片上的相关比赛规则知识，请用列表或画树状图的方法求甲、乙两人都抽到讲述本届运动会新增项目的有关比赛规则的概率．
20. (本小题8.0分)
“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标，第三阶段实现水稻亩产量1008公斤的目标．
(1)如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；
(2)按照(1)中亩产量增长率，科研团队期望第四阶段水稻亩产量达到1200公斤，请通过计算说明他们的目标能否实现．
21. (本小题8.0分)
如图，△ABC是⊙O的内接三角形，直径AB=6，∠BAC=2∠B，过点A的切线交OC的延长线于点D．
(1)求AD的长；
(2)求图中阴影部分面积．
22. (本小题8.0分)
【材料阅读】
先阅读理解下面的例题，再按要求解答下列问题：
我们知道a2≥0，所以代数式a2的最小值为0，可以用公式a2±2ab+b2=(a±b)2来求一些多项式的最小值．
例题：求代数式y2+4y+8的最小值．
解：y2+4y+8=y2+4y+4+4=(y+2)2+4．
∵(y+2)2≥0
∴(y+2)2+4≥4
∴代数式y2+4y+8的最小值为4．
请应用上述思想方法，解决下列问题：
【类比探究】
(x−2)2+2的最小值为______；
【举一反三】
代数式−x2+8x有最______(填“大”或“小”)值为______；
【灵活运用】
某农场计划建造一个矩形养殖场，为充分利用现有资源，该矩形养殖场一面靠墙(墙的长度为15m)，另外三面用栅栏围成，中间再用栅栏把它分成两个面积为1∶2的矩形．已知栅栏的总长度为24m，则可设较小矩形的宽为xm，较大矩形的宽为2xm(如图).当x为多少时，矩形养殖场的总面积最大？最大值为多少？
23. (本小题8.0分)
如图，PA为⊙O的切线，A为切点，过点A作AB⊥OP，垂足为点C，交⊙O于点B，延长BO与PA的延长线交于点D．
(1)求证：PB是⊙O的切线；
(2)若OB=3，OD=5，求DP的长．
24. (本小题8.0分)
如图，已知抛物线y=ax2+bx+c与x轴交于A(3,0)，B(1,0)两点，与y轴交于点C.且有OA=OC．
(1)求抛物线解析式；
(2)点P在抛物线的对称轴上，使得△ACP是以AC为底的等腰三角形，求出点P的坐标；
(3)在(2)的条件下，若点Q在抛物线的对称轴上，并且有
∠AQC=12∠APC，直接写出点Q的坐标．
答案和解析
1.【答案】D
【解析】解：“打开电视，正在播放云南卫视”是随机事件；
“一个盒子中装有5个黄球和2个红球，从中摸出一个球是黄球”是随机事件；
“任意一个三角形的内角和是360°”是不可能事件；
“一个图形旋转后所得的图形与原图形全等”是必然事件；
故选D．
2.【答案】D
【解析】解：中心对称图形是旋转180°能完全重合的图形，故D选项符合题意；故选D．
3.【答案】C
【解析】解：抛物线y=13(x−7)2+5的顶点坐标是(7,5)；
故选C．
4.【答案】C
【解析】解：∵四边形ABCD是⊙O的内接四边形，∠BCD=124°，
∴∠A=180°−124°=56°；
故选C．
5.【答案】B
【解析】解：化简二次函数：y=3x2−6x−9，
∵a=3>0，
∴二次函数的图象开口方向向上，故A错误；
当y=0时，0=3(x+1)(x−3)，
解得x1=−1,x2=3，
即与x轴的交点坐标为(−1,0)和(3,0)，故B正确；
对称轴是直线x=−−62×3=1，故C错误；
当x=0时，y=3×0+1×0−3=−9，故D错误；
故选B．
6.【答案】A
【解析】解：连接OB，OC，
∵ABCDEF是正六边形，
∴OA=OB=BC=6，
∴正六边形ABCDEF的周长为36．
故选A．
7.【答案】A
【解析】解：关于x的一元二次方程x2−2x−k=0有两个不相等的实数根，
则根的判别式Δ=b2−4ac=−22−4×1×−k=4+4k>0，
解得，k>−1，
故选A．
8.【答案】B
【解析】解：A.二次函数y=x2的图象向右平移2个单位长度得，y=x−22，
当x=2时，y=0，图象过(2,0)；
B.二次函数y=x2的图象向右平移1个单位长度，再向下平移2个单位长度得，y=x−12−2，
当x=2时，y=−1，图象不经过(2,0)；
C.二次函数y=x2的图象向下平移4个单位长度得，y=x2−4，
当x=2时，y=0，图象经过(2,0)；
D.二次函数y=x2的图象沿x轴翻折，再向上平移4个单位长度得，y=−x2+4，
当x=2时，y=0，图象经过(2,0)；
故选B．
9.【答案】A
【解析】解：设母线的长为R，
由题意得，πR=2π×12，
解得R=24，
∴母线的长为24cm，
故选A．
10.【答案】B
【解析】解：设衬衫的单价降了x元．
根据题意，得(40−x)(20+2x)=1250
故选B．
11.【答案】B
【解析】解：∵△ABC绕点C顺时针旋转得到△EDC，
∴CD=CB，∠B=∠EDC，
∴∠B=∠CDB=180°−70°2=55°，
∴∠EDC=55°，
∵∠ACB=90°，
∴∠ACD=90°−70°=20°，
∴∠EFC=∠ACD+∠EDC=20°+55°=75°．
12.【答案】C
【解析】解：∵y=ax2+bx+c(a≠0)图象的对称轴为直线x=−12，
∴b−2a=−12，即a=b>0，故②正确；
∵函数图象与y轴的交点在y轴负半轴
∴c<0
∴abc<0，故①错误；
当x=−3时，y=9a−3b+c>0，故③正确；
∵函数与x轴的一个交点坐标为−2,0 ，对称轴为直线x=−12，
∴与x轴的另一个交点坐标为(1,0)，
∴y=a+b+c=0，∴2a+c=0，故④正确；
∵函数图象与x轴有两个交点
∴ax2+bx+c=0有两个不相等实数根，故⑤错误；
综上：②③④正确．
故选C．
13.【答案】(−5,1)
【解析】解：点A(5,−1)关于原点的对称点为点B为(−5,1)．
故答案为：(−5,1)．
14.【答案】0.96
【解析】解：利用频率估计概率，根据表格任意抽取的一个头盔是合格产品的概率是0.96．
故答案为：0.96．
15.【答案】1
【解析】解：x1，x2是方程x2+3x−4=0的两个实数根，
则x1+x2=−3，x1·x2=−4，
则x1+x2−x1x2 =−3−(−4)=1．
故答案为：1．
16.【答案】45 或 25
【解析】解：如图，连接AO．
∵CD=10，OA=OC=5，OM:OC=3:5，
∴OM=3，
∵AB⊥CD，
∴OA2−OM2=AM=52−32=4，
∵C、D在弦AB的哪一侧位置不确定，
∴求弦AC的长需分如图两种情况．
当点C的位置如图①时，
在Rt△AMC中，AC=AM2+CM2=42+82=45(cm)．
当点C的位置如图②时，
在Rt△AMC中，AC=AM2+MC2=42+22=25(cm)．
17.【答案】解：(1) x2−4x−3=0 ，
∵a=1，b=−4，c=−3，
∴ Δ=b2−4ac=16−4×1×(−3)=16+12=28>0 ，
∴ x=−b±b2−4ac2a=4±272=2±7 ，
∴ x1=2+7 ， x2=2−7 ．
(2) 3x(x−2)−(x−2)=0 ，
(x−2)(3x−1)=0 ，
x−2=0或3x−1=0，
x1=2， x2=13．

【解析】见答案．
18.【答案】解：(1)如图所示， △A1B1C1 即为所求， B1(1,−1) ；
(2)如图所示， △A2B2C2 即为所求， C2(5,3) ．

【解析】见答案．
19.【答案】解：(1)14 ；
(2)列表分析如下：
∵共有12种等可能的结果，其中他们两人都抽到讲述本届运动会新增项目的有2种情况，分别是 A,B ， B,A ，
∴甲、乙两人都抽到讲述本届运动会新增项目的有关比赛规则的概率： 212=16 ，
即 P(甲,乙两人都抽到讲述本届运动会新增项目的有关比赛规则)=16 ．

【解析】见答案．
20.【答案】解：(1)设亩产量的平均增长率为x，
依题意得： 700(1+x)2=1008 ，
解得： x1=0.2=20％ ， x2=−2.2 (不合题意，舍去)．
答：亩产量的平均增长率为20%．
(2) 1008×(1+20％)=1209.6 (公斤)．
∵1209.6>1200，
∴他们的目标能实现．

【解析】见答案．
21.【答案】解：(1)∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠BAC+∠B=90°，
∵∠BAC=2∠B，
∴∠BAC=60°，∠B=30°，
∵AD是 ⊙O 的切线，
∴∠OAD=90°，
∴OD=2OA=6，
∴ AD=OD2−OA2=62−32=33 ．
(2) S阴影部分=S△OAD−S扇形AOC=12×33×3−60°π×32360°=932−32π．

【解析】见答案．
22.【答案】解：【类比探究】2．
【举一反三】大，16．
【灵活运用】
矩形养殖场的总面积是ym2 ，
根据题意知：较大矩形的宽为2xm，长为 24−x−2x3=(8−x)m ，
∵墙的长度为15m，
∴ 0根据题意得： y=(x+2x)(8−x)=−3x2+24x=−3(x−4)2+48 ，
∵ −3<0 ，
∴当x=4时，y取最大值，最大值为48，
答：当x=4时，矩形养殖场的总面积最大，最大值为48m2．

【解析】见答案．
23.【答案】(1)证明：连接OA，
∵AB⊥OP，OB=OA，∴∠BOP=∠AOP，
∵PA是 ⊙O 的切线，∴∠OAP=90°，
在 △OBP 与 △OAP 中，
{OB=OA∠BOP=∠AOPOP=OP ，
∴ △OBP≌△OAP(SAS) ，
∴∠OBP=∠OAP=90°，∴OB⊥PB，
∵OB是半径，∴PB是 ⊙O 的切线．
(2)解：∵OD=5，OA=OB=3，
在 Rt△AOD 中， AD=OD2−OA2=4 ，
∵PA、PB为 ⊙O 的切线，∴PA=PB，
在Rt△DBP中，PD2=PB2+BD2 ，即 (PB+4)2=PB2+82 ，
∴PB=6，∴PA=6，∴DP=PA+AD=6+4=10．

【解析】见答案．
24.【答案】解：(1)∵OA=OC， A(3,0) ，∴c=3
将点 A(3,0) ，B(1,0) 代入 y=ax2+bx+3 ，得
9a+3b+3=0a+b+3=0，解得a=1b=−4 ，
∴ y=x2−4x+3．
(2)∵ y=x2−4x+3=(x−2)2−1 ，
∴抛物线的对称轴为直线x=2，
设 P(2,t) ，∴ PA=1+t2 ， PC=4+(t−3)2 ，
∵ △ACP 是以AC为底的等腰三角形，∴PA=PC，
∴ 1+t2=4+(t−3)2 ，
解得t=2，∴ P(2,2)．
(3)Q点坐标为 2,−1 或 2,2+5 ．

【解析】(1)(2)见答案．
(3)∵ C(0,3) ， A(3,0) ， P(2,2) ，
∴CP=AP，
∴ △ACP 是等腰三角形，
∴∠APC的角平分线为PO，
∴∠CPO=∠APO，
如图1，当Q点在x轴下方时，过C点作 CQ//AP 交抛物线的对称轴为Q点，连接AQ，
∴∠CQP=∠QPA，
设直线AP的解析式为y=kx+b，
∴ 3k+b=02k+b=2 ，
解得 k=−2b=6 ，
∴ y=−2x+6 ．
∵ CQ//AP ，∴设直线CQ的解析式为 y=−2x+m ，
∴m=3，∴ y=−2x+3 ，
∴ Q(2,−1) ，∴QE=1，EA=1，
∴ △QEA 是等腰直角三角形，
∴∠EQA=45°，∵∠OPE=45°，
∴ ∠CQE+∠EQA=∠OPE+∠APE=12∠APC ，
∴ Q(2,−1) ．
如图2，当Q点在x轴上方时，
∵CP=AP，∴以P为圆心CP为半径作圆，当Q点在圆P上时， ∠CQA=12∠CPA ，
此时 QP=CP=5 ，
∴ Q(2,2+5) ，
综上所述：Q点坐标为 2,−1 或 2,2+5 ．
抽查的头盔数n
100
200
300
500
800
1000
3000
合格的头盔数m
95
194
289
479
769
960
2880
合格头盔的频率mn
0.950
0.945
0.962
0.958
0.961
0.960
0.960
甲
乙
A
B
C
D
A
A,B
A,C
A,D
B
B,A
B,C
B,D
C
C,A
C,B
C,D
D
D,A
D,B
D,C