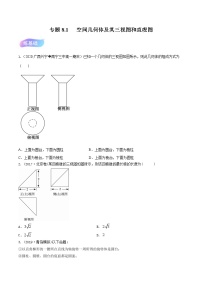
高考数学一轮复习 专题8.1 空间几何体及其三视图和直观图（练）

这是一份高考数学一轮复习 专题8.1 空间几何体及其三视图和直观图（练），文件包含专题81空间几何体及其三视图和直观图练教师版docx、专题81空间几何体及其三视图和直观图练学生版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。
高考数学一轮复习策略1、揣摩例题。课本上和老师讲解的例题，一般都具有一定的典型性和代表性。要认真研究，深刻理解，要透过“样板”，学会通过逻辑思维，灵活运用所学知识去分析问题和解决问题，特别是要学习分析问题的思路、解决问题的方法，并能总结出解题的规律。2、精练习题复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。3、加强审题的规范性每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。4、重视错题“错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。 专题8.1   空间几何体及其三视图和直观图1.（2020·广西兴宁�南宁三中高一期末）已知一个几何体的三视图如图所示，则此几何体的组成方式为（    ）A．上面为圆台，下面为圆柱 B．上面为圆台，下面为棱柱C．上面为棱台，下面为棱柱 D．上面为棱台，下面为圆柱【答案】A【解析】结合图形分析知上面为圆台，下面为圆柱.故选：A.2.（2021·江西师大附中高二月考（理））如图是一个棱锥的正视图和侧视图，它们为全等的等腰直角三角形，则该棱锥的俯视图不可能是（    ）A． B．C． D．【答案】C【解析】根据棱锥的三视图想象原几何体的结构，可以在正方体中想象描出原几何体，确定其结构．【详解】若几何体为三棱锥，由其正视图和侧视图可知，其底面在下方且为直角三角形，故ABD均有可能，若几何体是四棱锥，由其正视图和侧视图可知，其底面在下方，且为正方形，俯视图为正方形，但对角线应从左上到右下，C不正确．故选：C．3.（2021·江苏高一期末）已知一个圆锥的母线长为2，其侧面积为，则该圆锥的高为（    ）A．1 B． C． D．2【答案】C【解析】由侧面积求出圆锥的底面圆半径，再根据勾股定理可求得其高.【详解】设圆锥的底面圆的半径为 ，母线为，则，所以其侧面积为，解得，所以圆锥的高为.故选：C.4.（2020·河北易县中学高三其他（文））若圆台的母线与高的夹角为，且上、下底面半径之差为2，则该圆台的高为（    ）A． B．2 C． D．【答案】D【解析】设上、下底面半径分别为，，圆台高为，由题可知：，即，所以．故选：D5.（2020届浙江绍兴市诸暨市高三上期末）某几何体的正视图与侧视图如图所示：则下列两个图形①②中，可能是其俯视图的是（    ）A．①②都可能 B．①可能，②不可能C．①不可能，②可能 D．①②都不可能【答案】A【解析】若是①，可能是三棱锥；若是②，可能是棱锥和圆锥的组合；所以①②都有可能，故选：A.6．（2021·石家庄市第十七中学高一月考）如图，某沙漏由上、下两个圆锥组成，每个圆锥的底面直径和高均为，现有体积为的细沙全部漏入下圆锥后，恰好堆成一个盖住沙漏底部的圆锥形沙堆，则此锥形沙堆的高度为（    ）A． B． C． D．【答案】C【解析】根据圆锥的体积公式列方程求出沙堆的高．【详解】解：细沙漏入下部后，圆锥形沙堆的底面半径为，设高为，则沙堆的体积为，解得，所以圆锥形沙堆的高度为．故选：．7.（2021·云南弥勒市一中高一月考）如图，正方形的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是（    ）A．8 B．6 C． D．【答案】A【解析】根据斜二测画法的规则，得到原图形的形状为平行四边形，进而求得其边长，即可求解.【详解】由斜二测画法的规则，可得原图形为是一个平行四边形，如图所示，因为水平放置的一个平面图形的直观图的边长为1的正方形，可得，所以原图形中，在直角中，可得，所以原图形的周长为.故选：A.8．（2021·浙江高三三模）如图，等腰直角三角形在平面上方，，若以为旋转轴旋转，形成的旋转体在平面内的投影不可能的是（    ）A． B． C． D．【答案】C【解析】对直线与平面的位置关系进行分类讨论，判断出投影的形状，即可得出合适的选项.【详解】若，则形成的旋转体在平面内的投影如D选项所示；若，则形成的旋转体在平面内的投影为正方形；若与所成的角的取值范围是时，则形成的旋转体在平面内的投影如A、B选项所示.投影不可能如C选项所示.故选：C.9．（2020·上海市进才中学高二期末）设是半径为的球的直径，则两点的球面距离是________．【答案】【解析】是半径为的球的直径，则两点所对的球心角为，球面距离为．故答案为：．10．（2020·全国）如图为一几何体的平面展开图，按图中虚线将它折叠起来，画出它的直观图．【答案】见解析【解析】由题设中所给的展开图可以得出，此几何体是一个四棱锥，其底面是一个边长为2的正方形，垂直于底面的侧棱长为2，其直观图如图所示.1.（2021·四川高一期末（理））某圆柱的高为，底面周长为，其三视图如图.圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从到的路径中，最短路径的长度为（    ）A． B． C． D．【答案】B【解析】根据三视图分析出所在的位置，然后结合圆柱的侧面展开图即可求出结果.【详解】由三视图还原几何体，如图：即点在距离点在底面投影的圆弧 处，沿所在的母线得到如图所示的侧面展开图， 圆柱的底面周长即为侧面展开图的长，圆柱的高即为侧面展开图的宽，而线段的距离即为所求到的路径中的最短路径，因为底面周长为 ,所以，又因为高为，则，所以,故选：B.2.【多选题】（2021·宁波市北仑中学高一期中）如图，棱长为的正四面体形状的木块，点是的中心．劳动课上需过点将该木块锯开，并使得截面平行于棱和，则下列关于截面的说法中正确的是（    ）A．截面不是平行四边形B．截面是矩形C．截面的面积为D．截面与侧面的交线平行于侧面【答案】BCD【解析】过点构建四边形，通过相关直线间的平行关系进一步证明为平行四边形，找对应线之间的垂直证明截面为矩形，从而计算截面面积【详解】解：如图所示，在正四面体中，4个面均为正三角形，由于点为的中心，所以位于的中线的外，分别取的三等分点，则∥，∥，∥，∥，所以∥，∥，所以截面为平行四边形，所以A错误，延长交于，连接，由于为的中心，所以为的中点，因为，所以，因为，所以平面，所以，因为∥，∥，所以，所以截面为矩形，所以B正确， 因为，所以，所以C正确，对于D，截面平面，∥，平面，平面，所以∥平面，所以D正确，故选：BCD3.（2021·湖北随州市·广水市一中高一月考）如图所示，矩形是水平放置一个平面图形的直观图，其，，则原图形是（    ）A．正方形B．矩形C．菱形D．梯形【答案】C【解析】由已知得原图为平行四边形，，利用勾股定理计算边长得到,可判断原图形的形状.【详解】因为，，所以直观图还原得，，四边形为平行四边形，，则，，，，，所以，故原图形为菱形．故选：C.4．（2021·肇州县第二中学高一月考）如图是利用斜二测画法画出的的直观图，已知，且的面积为16，过点作轴于点，则的长为（    ）A． B． C． D．1【答案】A【解析】利用面积公式，求出直观图的高，求出，然后在直角三角形中求解即可【详解】解：由直观图可知，在中，，因为的面积为16，,所以，所以，所以，因为， 轴于点，所以，故选：A5．（2021·宁夏大学附属中学高一月考）三棱锥及其三视图中的正视图和侧视图如图所示，则棱的长为（  ）A． B．C． D．【答案】B【解析】根据几何体的三视图，结合几何体的数量关系，在直角中，即可求解.【详解】如图所示，根据三棱锥及其三视图中的正视图和侧视图，可得底面中，点为的中点， ，且底面，又由点为的中点，且根据侧视图，可得，在直角中，可得 又由，在直角中，可得.故选：B.6．（2021·江苏省镇江中学）点是平面外一点，且，则点在平面上的射影一定是的（    ）A．外心 B．内心 C．重心 D．垂心【答案】A【解析】过点作平面，因为，得到，即可求解.【详解】如图所示，过点作平面，可得 因为，可得，所以为的外心.故选：A.7.（2021·上海高二期末）圆锥的高为1，底面半径为，则过圆锥顶点的截面面积的最大值为____________【答案】2【解析】求出圆锥轴截面顶角大小，判断并求出所求面积最大值．【详解】如图，是圆锥轴截面，是一条母线，设轴截面顶角为，因为圆锥的高为1，底面半径为，所以，，所以，，设圆锥母线长为，则，截面的面积为，因为，所以时，．故答案为：2．8．（2021·浙江绍兴市·高一期末）已知四面体的所有棱长均为4，点满足，则以为球心，为半径的球与四面体表面所得交线总长度为______.【答案】【解析】根据正四面体的结构特征求得到面的距离，进而利用球的截面的性质求得各面所在平面与球的截面圆的半径，注意与各面的三角形内切圆的半径比较，确定此截面圆是否整个在面所在的三角形内，进而确定球与各面的交线，得到球与四面体表面所得交线总长度．【详解】已知四面体ABCD的所有棱长均为4，所以四面体ABCD是正四面体，因为点O满足，所以为正四面体ABCD的中心设正三角BCD的中心为F，正三角ACD的中心为G，CD的中点为E，则连接则．
则，，，
．
因为球O的半径为，所以球O被平面截得圆半径为，
因为正三角形BCD的边长为4，所以正三角形内切圆半径为，故球O与四面体ABCD的每一个面所得的交线为正好为内切圆，每个内切圆的周长为，所以球与四面体ABCD表面所得交线总长度．
故答案为：．9.（2020届浙江杭州四中高三上期中）某几何体的三视图如图所示，且该几何体的体积是3，则正视图中的x的值是_____，最长棱长为_____．【答案】        【解析】由已知中的三视图可得该几何体是一个以直角梯形为底面的四棱锥，且梯形上下边长为1和2，高为2，如图：，，，，，平面，，∴底面的面积，∴几何体的体积，可得，最长棱长为：，故答案为：；．10．（2019·全国高考真题（理））中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．【答案】共26个面.    棱长为.    【解析】由图可知第一层与第三层各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有个面．如图，设该半正多面体的棱长为，则，延长与交于点，延长交正方体棱于，由半正多面体对称性可知，为等腰直角三角形，，，即该半正多面体棱长为．1.（2021·全国高考真题）已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为（    ）A． B． C． D．【答案】B【解析】设圆锥的母线长为，根据圆锥底面圆的周长等于扇形的弧长可求得的值，即为所求.【详解】设圆锥的母线长为，由于圆锥底面圆的周长等于扇形的弧长，则，解得.故选：B.2．（2021·北京高考真题）定义：24小时内降水在平地上积水厚度（）来判断降雨程度．其中小雨（），中雨（），大雨（），暴雨（），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（ ）A．小雨 B．中雨 C．大雨 D．暴雨【答案】B【解析】计算出圆锥体积，除以圆面的面积即可得降雨量，即可得解.【详解】由题意，一个半径为的圆面内的降雨充满一个底面半径为，高为的圆锥，所以积水厚度，属于中雨.故选：B.3.（2020·全国高考真题（理））如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为，在俯视图中对应的点为，则该端点在侧视图中对应的点为（    ）A． B． C． D．【答案】A【解析】根据三视图，画出多面体立体图形，上的点在正视图中都对应点M,直线上的点在俯视图中对应的点为N,∴在正视图中对应,在俯视图中对应的点是,线段,上的所有点在侧试图中都对应,∴点在侧视图中对应的点为.故选：A4．(2019年高考全国Ⅲ卷理)如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则(    )A．BM=EN，且直线BM，EN 是相交直线
B．BM≠EN，且直线BM，EN 是相交直线
C．BM=EN，且直线BM，EN 是异面直线D．BM≠EN，且直线BM，EN 是异面直线【答案】B【解析】如图所示，作于，连接，BD，易得直线BM，EN 是三角形EBD的中线，是相交直线.过作于，连接，平面平面，平面，平面，平面，与均为直角三角形．设正方形边长为2，易知，，，故选B．5.（2018·北京高考真题（文））某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（   ）A.1 B.2C.3 D.4【答案】C【解析】分析：根据三视图还原几何体，利用勾股定理求出棱长，再利用勾股定理逆定理判断直角三角形的个数.详解：由三视图可得四棱锥，在四棱锥中，，由勾股定理可知：，则在四棱锥中，直角三角形有：共三个，故选C.6.（2021·全国高考真题（理））以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为_________（写出符合要求的一组答案即可）．【答案】③④（答案不唯一）【解析】由题意结合所给的图形确定一组三视图的组合即可.【详解】选择侧视图为③，俯视图为④，如图所示，长方体中，，分别为棱的中点，则正视图①，侧视图③，俯视图④对应的几何体为三棱锥.故答案为：③④.