数学七年级上册2.4 绝对值教学演示课件ppt

这是一份数学七年级上册2.4 绝对值教学演示课件ppt，文件包含24绝对值pptx、华东师大版中学数学七年级上第2章有理数24绝对值教学详案docx等2份课件配套教学资源，其中PPT共16页， 欢迎下载使用。
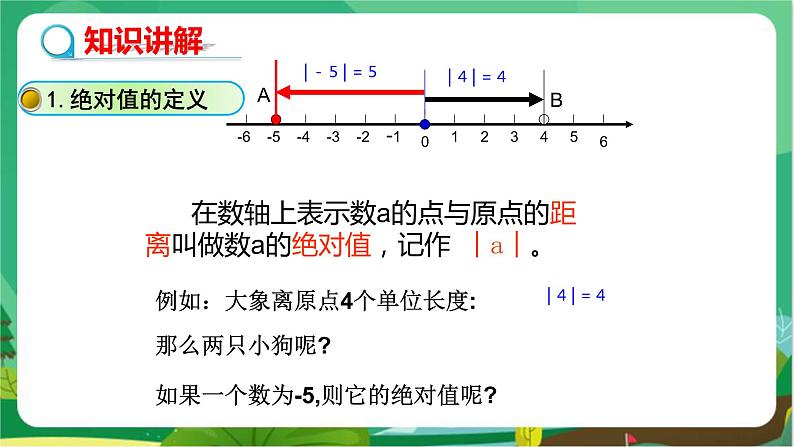
第2章　有理数2.4　绝对值教学目标1.使学生掌握绝对值的几何意义和代数意义，会求一个数的绝对值.2.通过观察、比较、探索、分析和归纳等过程，使学生学会合作、交流，渗透数形结合的数学思想，培养学生运用知识分析问题和解决问题的能力.教学重难点重点：求一个已知数的绝对值及正确理解绝对值的概念.难点：对绝对值的几何意义、代数定义的导出，对“负数的绝对值是它的相反数”的理解.教学过程复习巩固1.分别求出和的相反数.2.化简下列各题：（1）；       　　　（2）； （3）-［+（-1）］；       　（4）-{-［-（+5）］}.导入新课小红和小明从同一处O出发,分别向东、西方向行走10米,他们行走的路线　　　　,他们行走的距离　　　　. (填“相同”或“不相同”) 由以上问题知道,10到原点的距离是　　　　,-10到原点的距离是　　　，到原点的距离等于10的数有　　　　个,它们的关系是一对　　　　. （学生根据要求回答）不相同，相同，10，10，两，相反数【教学说明】通过复习引入，让学生自主独立完成，既巩固了前面所学知识，又自然引入了本节课知识的探究，同时学生对以上问题解决起来难度不大，也增强了学生学习的信心.探究新知合作探究1.绝对值的定义问题：在数轴上画出和，观察：（1）和分别于原点的位置关系是什么？它们在原点的两侧, 且到原点的距离相等.（2）和到原点的距离是多少？          6小结：在讨论数轴上的点与原点的距离时，只需观察它与原点之间相隔多少个单位长度，与位于原点何方无关.思考：请同学们想一想：如何表示一个数到原点的距离呢？（学生讨论解答，教师总结）【总结】定义：把在数轴上表示数的点与原点的距离叫做数的绝对值，记做.例如，在数轴上表示数-6与表示数6的点与原点的距离都是6，所以-6和6的绝对值都是6，记作|-6|＝|6|＝6.同样可知|-4|＝4，|+1.7|＝1.7.2.绝对值的特点试一试：你能从中发现什么规律? 由绝对值的意义，我们可以知道：(1)|+2|＝  2  ，＝，|+8.2|＝  8.2  ； (2)|0|＝  0  ；(3)|-3|＝  3  ，|-0.2|＝  0.2  ，|-8.2|＝  8.2  .（学生讨论解答，教师总结）【问题探索】通过对具体数的绝对值的讨论，并注意观察在原点右边的点表示的数（正数）的绝对值有什么特点？在原点左边的点表示的数（负数）的绝对值又有什么特点？【总结】绝对值的性质：1.一个正数的绝对值是它本身；2.0的绝对值是0；3.一个负数的绝对值是它的相反数.即：①若a＞0，则|a|＝a；②若a＜0，则|a|＝–a；③若a＝0，则|a|＝0；  或写成：3.绝对值的非负性由绝对值的定义可知：不论有理数a取何值，它的绝对值总是正数或0(通常也称非负数)，绝对值具有非负性，即|a|≥0.例1  求下列各数的绝对值：，+，-4.75，10.5.解：＝；＝；|-4.75|＝4.75；|10.5|＝10.5.例2  化简：（1）； （2）.解：（1） ；    （2） .例3  计算：（1）|0.32|+|0.3|；（2）|–4.2|–|4.2|；（3）–.解：（1）0.62；       （2）0；       （3）.【总结】求一个数的绝对值必须先判断这个数是正数还是负数，然后由绝对值的性质得到.在（3）中要注意区分绝对值符号与括号的不同含义.课堂练习1.判断：（1）一个数的绝对值是9 ，则这个数是9.　　(     )  （2）|5|＝|-5|.　　　　　　　　　　　　　　 (     ) （3）|-0.5|＝|0.5|.　　　　　　　　　　　　　(     )（4）|3|＞0. 　　　　　　　　　　　　　　　(     ) （5）|-1.2|＞0. 　　　　　　　　　　　　　　(     ) （6）有理数的绝对值一定是正数.       　   (     ) 　（7）若a＝-b，则|a|＝|b|.                 (     )  　　　　　　　　  （8）若|a|＝|b|，则a＝b.                  (     ) （9）若|a|＝-a，则a必为负数.            (     ) （10）互为相反数的两个数的绝对值相等.   (     ) 2. 如果a与1互为相反数，则|a|等于（    ）A.2　　　　　　　B. -2　　　　　　　C.1　　　　　　　D.-13.-|-4|＝（    ）A.-4　　　　　　 B.              C.             D.44.填空：| m|＝        (m＜0) ；| a- b | ＝         （a＞b）.参考答案1.×√√√√×√××√2.C3.A4.-m    a-b课堂小结1.对绝对值概念的理解可以从其几何意义和代数意义两方面考虑，从几何方面看，一个数a的绝对值就是数轴上表示数a的点与原点的距离，它具有非负性；从代数方面看，一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，0的绝对值是0.2.求一个数的绝对值注意先判断这个数是正数还是负数.布置作业教材24-25页　习题2.4　第1，2，3，4题板书设计第2章　有理数2.4　绝对值1.绝对值的定义.2.性质:|a|＝ 3.非负性:|a|≥0.教学反思                                     教学反思                                          教学反思