湘教版七年级上册1.5.1有理数的乘法图文ppt课件

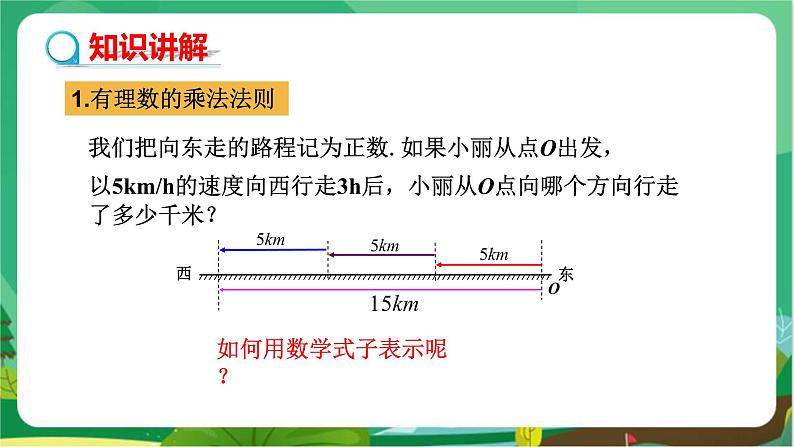
教学目标

1.理解有理数的乘法法则，能说出有理数乘法的符号法则.

2.能熟练进行有理数的乘法运算.

3.经历有理数乘法法则的观察、思考、抽象过程，体会有理数乘法法则规定的合理性.

教学重难点

重点:有理数的乘法运算．

难点:有理数乘法法则的理解．

教学过程

导入新课

我们先来复习一下前面所学的知识.

1.点名学生计算:(-2)+(-2)+(-2).

2.教师:你们知道有理数包括哪些数吗?小学学习的四则运算是在有理数的什么范围内进行的?(非负数)

学生讨论并发言.

3.教师:在有理数的加减运算中,关键问题是什么?和小学所学的运算最主要的不同点是什么?(符号问题)

学生讨论并发言.

4.根据有理数加减运算中引出的新问题主要是负数加减,运算的关键是确定符号问题,你能不能猜出在有理数乘法以及以后学习的除法中将引出的新内容以及关键问题是什么?(负数问题,符号的确定)

探究新知

探究　有理数的乘法法则

问题1：我们把向东走的路程记为正数.如果小丽从点O出发，以5 km/h的速度向东行走3 h后，小丽从O点向哪个方向行走了多少千米？

这个问题可用乘法来解答:5×3＝15①

即小丽位于原来位置的东方15米处.

问题2:如果小丽从点O出发，以5 km/h的速度向西行走3 h后，小丽从O点向哪个方向行走了多少千米？结果有何变化？

这也不难,写成算式就是（-5）×3＝-15，②

即小丽位于原来位置的西方15米处.

师生活动

通过观察以上题目，归纳总结有理数相乘的法则.

【归纳】比较上面两个算式，当我们把“5×3＝15”中的一个因数“5”换成它的相反数“-5”时,所得的积是原来的积“15”的相反数“-15”.

一般地,我们有:把一个因数换成它的相反数,所得的积是原来的积的相反数.

【推广】应用此结论,5×(-3)＝?　(-5)×(-3)＝?　

(学生答)把5×(-3)和①式对比,这里把一个因数“3”换成了它的相反数“-3”,所得的积应是原来的积“15”的相反数“-15”,即5×(-3)＝-15.把(-5)×(-3)和②式对比,这里把一个因数“3”换成了它的相反数“-3”,所得的积应是原来的积“-15”的相反数“15”,即(-5)×(-3)＝15.此外,把(-5)×0＝0同5×0＝0作比较.

【总结】引导学生自己归纳有理数乘法的法则:

两数相乘,同号得正,异号得负,并把绝对值相乘;

任何数与0相乘仍得0.

【强调】“同号得正”中正数乘以正数得正数就是小学时期学习的乘法,有理数中特别注意“负负得正”和“异号得负”.

有理数乘法法则与小学学习的乘法相比,由于介入了负数,使乘法变得较复杂了,但并不难,关键仍然是乘法的符号法则:“同号得正,异号得负”,符号一旦确定,就归结为小学的乘法了.

因此,在进行有理数乘法运算时更需时时强调:先定符号后定值.

新知应用

【例1】计算:

(1)(-5)×(-6)；　　　(2)×；

(3)×； (4)8×(-1.25).

【解】(1)(-5) ×(-6)＝+(5×6)＝30.

(2)×＝＝-.

(3)×＝＝1.

(4)8×(-1.25)＝-(8×1.25)＝-10.

【例2】用正负数表示气温的变化量,上升为正,下降为负,登山队攀登一座山峰,每向上攀登1 km气温的变化量为-6 ℃,向上攀登3 km后气温有什么变化?学生口述,教师板书.

通过上面的学习，思考并讨论下面的问题:

(1)若a＜0,b＞0,则ab____0 ；

(2)若a＜0,b＜0,则ab____0 ；

(3)若ab＞0,则a，b应满足什么条件？

(4)若ab＜0,则a，b应满足什么条件？

【解】（1）＜   （2）＞      （3） a，b同号.        （4）a，b异号.

课堂练习

1．填表：

2．计算3×(-2)的结果是（    ）

A.5             B.-5              C.6           D.-6

3．下列算式中，积为正数的是（    ）

A.       B.       C.      D.

4．若ab>0，则必有（    ）

A. a>0，b>0                        B. a<0，b<0     

C. a>0，b<0                        D. a>0，b>0或a<0，b<0

5．若ab＝0，则一定有（    ）

A. a＝b＝0                         B. a，b至少有一个为0     

C. a＝0                            D. a，b最多有一个为0

6.计算：

（1）；      （2）；

（3）； （4）.

参考答案

1.

2.D  

3.B 

4.D  

5.B  

6.解：（1）＝       

（2）＝＝.

（3）＝＝2.

（4）＝0.

课堂小结

1.有理数乘法法则：

两数相乘，同号得正，异号得负，并把绝对值相乘.

任何数同0相乘，都得0.

2.有理数乘法的求解步骤：

有理数相乘，先确定积的符号，再确定积的绝对值.

布置作业

教材 第31页  练习  第1，2题.

板书设计

第1章 有理数

1.5  有理数的乘法和除法

1.5.1  有理数的乘法

第1课时　有理数的乘法

1.有理数乘法法则：

两数相乘，同号得正，异号得负，并把绝对值相乘.

任何数同0相乘，都得0.

2.有理数乘法的求解步骤：

有理数相乘，先确定积的符号，再确定积的绝对值.

教学反思

教学反思

教学反思

教学反思