初中数学湘教版七年级上册4.3.1角与角的大小比较课文配套ppt课件

教学目标

1.在现实情境中，认识角是一种基本的几何图形，理解角的两种概念，学会表示角的方法.

2.掌握角的大小比较方法.

3.理解角的平分线的定义，并会进行有关角的推理与计算.

4.体会角在实际生活中的作用，培养学生参与数学学习活动的热情和对数学的好奇心.

教学重难点

重点：会用不同的方法表示同一个角；比较角的大小，认识角的大小关系；认识角的平分线及画角的平分线.

难点：角的表示，比较两个角的大小.

教学过程

导入新课

小学里我们已经学过与角有关的简单知识，也知道角是一种基本图形，并且在我们周围的事物中存在着各种各样的角，如图，钟面上的时针与分针、圆规的两只脚之间、折扇的扇骨与扇骨之间都给我们以什么样的形象？

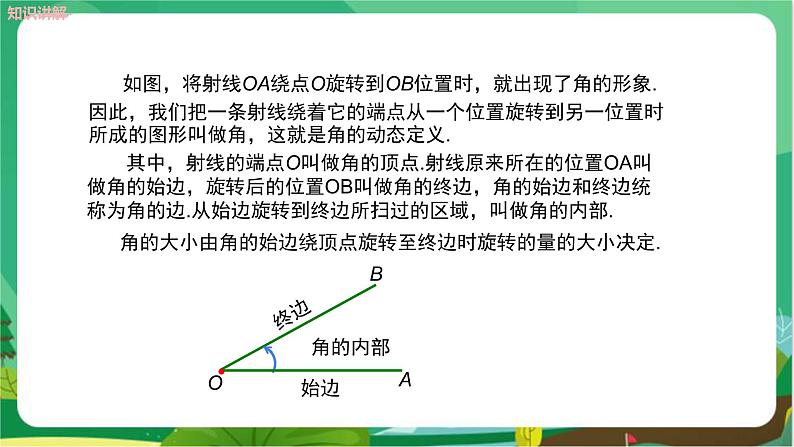
学生活动：进行独立思考、画图，然后观看教师的演示过程.

教师活动：用多媒体演示如何得到平面图形——角.

板书：角.

探究新知

探究一 角的概念

(1)提出问题：

从上面的活动过程中，你知道角是由什么图形组成的吗？

学生回答：两条射线.

教师活动：归纳角的定义、板书.

角的定义：角是由具有公共端点的两条射线组成的图形.这就是角的静态定义.

(2)通过运动的观点归纳角的定义.

教师活动：通过演示得出角的动态定义，角也可以看作由一条射线绕着它的端点旋转而形成的图形.

如图，将射线OA绕点O旋转到OB位置时，就出现了角的形象.  因此，我们把一条射线绕着它的端点从一个位置旋转到另一位置时所成的图形叫做角，这就是角的动态定义.

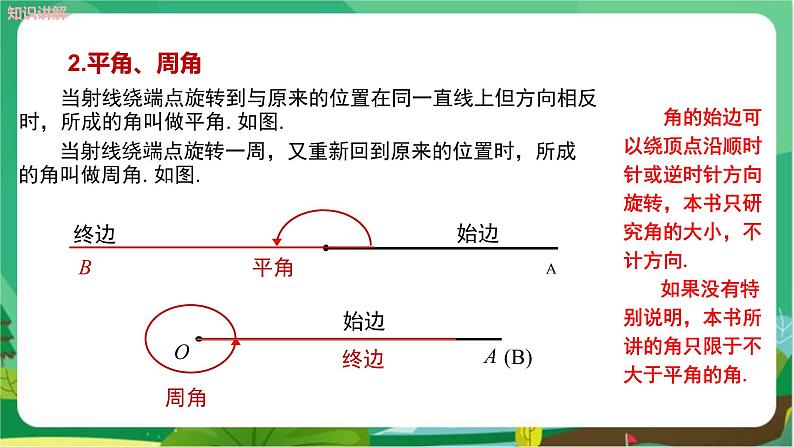
教师继续补充讲解有关概念

射线的端点O叫做角的顶点.射线原来所在的位置OA叫做角的始边，旋转后的位置OB叫做角的终边，角的始边和终边统称为角的边.从始边旋转到终边所扫过的区域，叫做角的内部.

角的大小由角的始边绕顶点旋转至终边时旋转的量的大小决定.

探究二 平角与周角

学生活动：阅读教材第124页有关内容，了解周角、平角的概念.

教师活动：参与学生交流，并用多媒体演示平角、周角的形成过程，启发、引导学生进行探索，并对学生的讨论结果进行评价.

从角的动态定义出发，得到平角、周角(如图所示)的定义.

当射线绕端点旋转到与原来的位置在同一直线上但方向相反时，所成的角叫做平角.如图①.

当射线绕端点旋转一周，又重新回到原来的位置时，所成的角叫做周角.如图②.

①                               ②

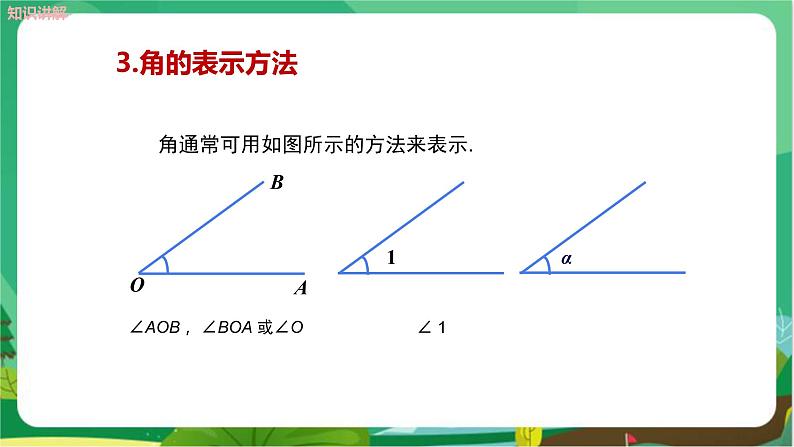
探究三 角的表示

(1)角的表示方法

学生活动：阅读教材第124页有关内容，了解角的表示方法.

教师活动：讲解角的不同表示方法，着重讲解一个顶点处有多个角的表示方法.

角用符号“∠”表示，读作“角”，通常的表示方法如下：

①用三个大写字母表示，如图中的角表示为∠ABC(或∠CBA)，中间字母B表示顶点，其他两个字母A，C分别表示角的两边上的点.注意表示顶点的字母必须写在中间.

②用一个数字或一个小写希腊字母(如α，β，γ)表示，如图中的角分别可表示为∠1，∠α，∠β等.(注意读法)

用一个小写希腊字母表示角的方法是在角的内部靠近角的顶点处画一条弧线，写上一个小写希腊字母，如α，记作∠α，读作角α.

用一个数字表示角的方法是在角的内部靠近角的顶点处画一条弧线，写上一个数字，如1，记作∠1，读作角1.在一个顶点处有较多角的情况下，也可以这样表示.

③角也可以用一个大写字母表示，这个大写字母是这个角的顶点.要注意的是，当两个或两个以上的角共用一个顶点时，不能用一个大写字母表示角.

注意：(1)不要混淆角的符号“∠”与小于号“＜”.

(2)几种角的表示方法的优缺点：①用三个大写英文字母表示，适用于所有的角，但比较繁琐；②用顶点处的一个大写字母来表示角比较简便，但只能用来表示以这个点为顶点的角只有一个的情况；③用数字或小写希腊字母来表示角比较简便，但需在图中标出相应的数字或小写希腊字母，另外当要表示的角较多且较集中时，会让人有一种眼花缭乱的感觉.

(3)在具体表示一个角时，首先用顶点字母表示，若不行，再选用数字或小写希腊字母来表示.至于用三个大写英文字母来表示，一要会用，即顶点字母在三个英文字母的中间，二要少用，因为这种方法较为繁琐.

探究四 角的大小比较的方法

问题1：怎样比较图中的∠ABC 和∠DEF的大小？

类比线段长短的比较，你认为应该如何比较两个角的大小?比较它们的大小，并说明你是怎么比较的.

师生活动

学生讨论解决问题的方法，学生代表展示交流.

学生展示交流后提问：比较角的大小的方法有几种?每种方法中应注意的问题是什么?

教师在学生展示交流的基础上，利用课件动画演示用量角器量角、用叠合法比较角的大小的过程，归纳操作要点.

用量角器量角时要注意：对中，重合，读数.

叠合两角时要注意：

(1)重合(两角的顶点及一边重合)；

(2)同旁(另一边落在第一条边的同旁).

追问：两个角的大小关系有几种?你能用图形和符号表示吗?

师生活动

学生画出图形，并用符号表示，指出两个角的大小关系有三种情况.

教师关注：学生运用度量法、叠合法比较角的大小时操作的规范性；学生是否能体会两个角的大小关系的三种情况.

探究五 角的平分线

师生活动

画出图形，如图所示，明确角平分线的概念.

①                              ②

提出问题：(1)你能用符号表示图①中角之间的关系吗?

(2)类比角的平分线，还有角的三等分线(如图②所示)，一个角的三等分线有几条?四等分线呢?

注意：角的平分线是一条射线，不是线段，也不是直线，它必须满足下面的两个条件：(1)是从角的顶点引出的射线，且在角的内部；(2)把已知角分成了两个角，且这两个角相等.

如何得到一个角的平分线?

师生活动

画图展示交流，教师结合学生的展示交流或利用课件动画演示折叠过程.

归纳方法(用量角器、折纸)：

(1)借助量角器画图：以已知角的顶点为顶点，已知角的一边为边，在已知角的内部画一个度数等于已知角度数一半的角，则这个角的另一边就是已知角的平分线.

(2)用折叠方法：把角沿顶点对折，使角的两边重合，沿折痕在角的内部画一条射线即为已知角的平分线.

教师关注：学生操作是否规范.

新知应用

例1   (角的表示方法)

写出如图所示的符合下列条件的角.

(1)能用一个大写英文字母表示的角.

(2)以A为顶点的角.

(3)图中所有小于平角的角(可用简便方法表示).

解：(1)∠B，∠C.

(2)∠1或∠CAD，∠2或∠DAB，∠CAB.

(3)∠C，∠1，∠2，∠CAB，∠B，∠3，∠4.

注意：表示角时，能用简便方法表示的要用简便方法表示，在一个顶点处有两个或两个以上的角时，不能用表示顶点的字母表示这个角.

例2　如图，OB是∠AOC的平分线，OD是∠COE的平分线.

（1）如果∠AOC＝80°，那么∠BOC是多少度？

（2）如果∠AOE＝140°，∠COD＝30°，那么∠AOB是多少度？

解：（1）∵ OB平分∠AOC，∠AOC＝80°，

∴ ∠BOC＝∠AOC＝×80°＝40°. 

（2）∵ ∠COD＝30°，OD平分∠COE，

∴ ∠COE＝2∠COD＝60°，

∴ ∠AOC＝∠AOE-∠COE＝140°-60°＝80°.

又∵ OB平分∠AOC，

∴ ∠AOB＝∠AOC＝×80°＝40°. 

课堂练习

1.下列说法正确的是  (    )

①两条射线所组成的图形叫角；

②角的大小与边的长短无关；

③角的两边可以一样长，也可以一长一短；

④角的两边是两条射线.

A. ①②                  B. ②④ 

C. ②③                  D. ③④

2.下列角中，能用∠1，∠ACB，∠C三种方法表示同一个角的是（   ）

A                   B           

C                   D

3.对于如图所示的各个角，用“>”“<”或“＝”填空：

∠AOB　　　　　∠AOC，

∠DOB　　　　　∠BOC，

∠BOC　　　　　∠AOD，

∠AOD　　　　　∠BOD.

4.如图，写出所有小于平角的角.

5.如图，（1）在∠AOB内部画1条射线OC，则图①中有　　　个不同的角；

（2）在∠AOB内部画2条射线OC，OD，则图②中有　　　个不同的角；

（3）在∠AOB内部画3条射线OC，OD，OE，则图③中有　　　个不同的角；

（4）在∠AOB内部画n条射线OC，OD，OE，…，则图中有　　　　个不同的角.

①                ②                ③

参考答案

1.B   

2.C   

3.<   >   <   >

4.解：小于平角的角有∠B，∠C，∠BAD，∠DAC，∠BAC，∠ADC，∠BDA，共七个角.

5.（1）3  （2）6  （3）10  （4）

课堂小结

1.什么是角？组成角的图形是什么？如何表示一个角？

2.本节课还复习了平角、周角，怎样得到这两种角？

3.角的大小比较的方法有哪些？

4.什么是角的平分线？有什么性质？

布置作业

教材125页练习第1，2题.

板书设计

第4章  图形的认识

4.3  角

4.3.1  角与角的大小比较

1.角的概念             　　  

静态定义：                   

动态定义：

2.平角与周角

3.角的表示方法

4.角的大小比较的方法

5.角的平分线

教学反思

教学反思

教学反思

教学反思

教学反思

教学反思