人教版九年级上册24.1.1 圆课时作业

这是一份人教版九年级上册24.1.1 圆课时作业，共8页。试卷主要包含了圆的定义，圆的性质，两圆的性质，与圆有关的角，圆和圆的位置关系等内容，欢迎下载使用。
第29课  《圆》全章复习与巩固课程标准1．理解圆及其有关概念，理解弧、弦、圆心角的关系，探索并了解点与圆、直线与圆、圆与圆的位置关系，探索并掌握圆周角与圆心角的关系、直径所对的圆周角的特征；
　　2．了解切线的概念，探索并掌握切线与过切点的半径之间的位置关系，能判定一条直线是否为圆的切线，会过圆上一点画圆的切线；
　　3．了解三角形的内心和外心，探索如何过一点、两点和不在同一直线上的三点作圆；
　　4．了解正多边形的概念，掌握用等分圆周画圆的内接正多边形的方法；会计算弧长及扇形的面积、圆锥的侧面积及全面积；
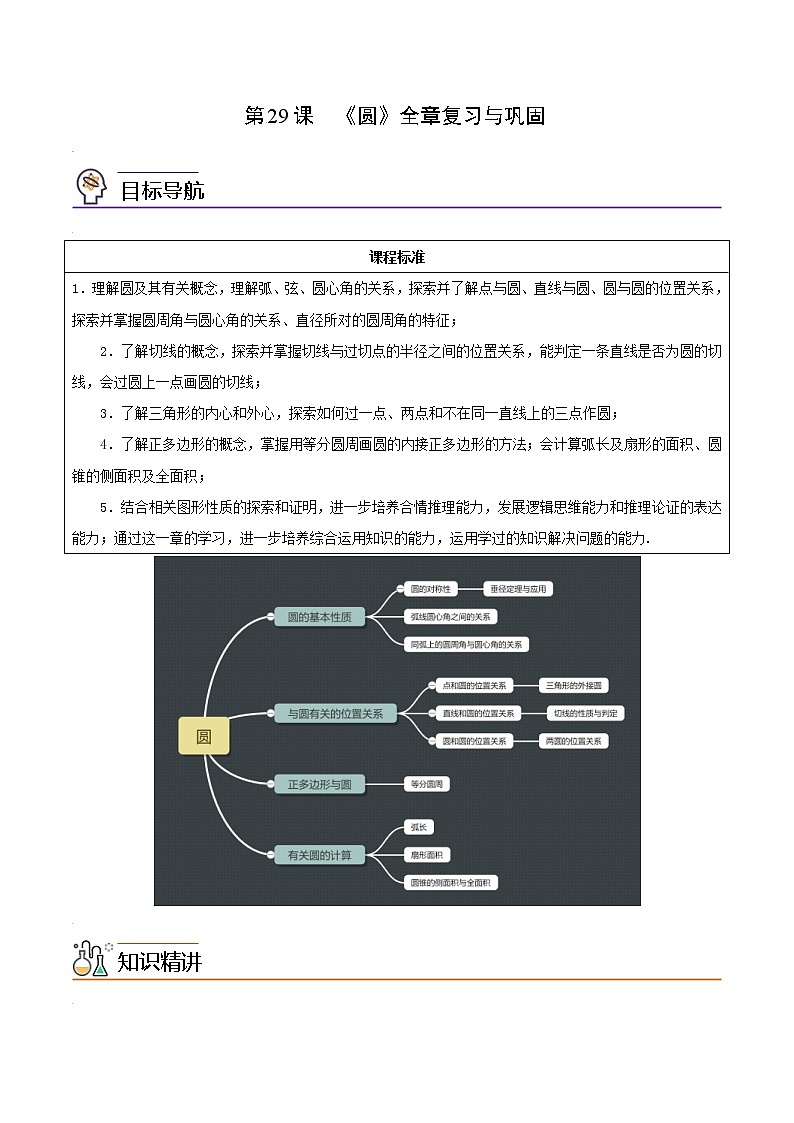
　　5．结合相关图形性质的探索和证明，进一步培养合情推理能力，发展逻辑思维能力和推理论证的表达能力；通过这一章的学习，进一步培养综合运用知识的能力，运用学过的知识解决问题的能力.知识点01  圆的定义、性质及与圆有关的角1．圆的定义
　　(1)线段OA绕着它的一个端点O            ，另一个端点A所形成的封闭曲线，叫做圆.
　　(2)圆是                              的集合.
要点诠释：
　  ①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可；
  　②圆是一条封闭曲线.2．圆的性质
　　(1)旋转不变性：圆是            图形，绕圆心旋转任一角度都和原来图形重合；圆是            对称图形，对称中心是圆心.
　　 　在同圆或等圆中，             ，这四组量中的任意一组相等，那么它所对应的其他各组分别相等.
　　(2)轴对称：圆是             图形，             都是它的对称轴.
　　(3)垂径定理及推论：
　　 　①                               .
　　 　②平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧.
　　 　③弦的垂直平分线过圆心，且平分弦对的两条弧.
　　 　④平分一条弦所对的两条弧的直线过圆心，且垂直平分此弦.
　　 　⑤平行弦夹的弧相等.
要点诠释：
     在垂经定理及其推论中：过圆心、垂直于弦、平分弦、平分弦所对的优弧、平分弦所对的劣弧，在这五个条件中，知道任意两个，就能推出其他三个结论.（注意：“过圆心、平分弦”作为题设时，平分的弦不能是直径）3．两圆的性质
　　(1)两个圆是一个轴对称图形，对称轴是两圆连心线.
　　(2)相交两圆的连心线垂直平分公共弦，相切两圆的连心线经过切点.4．与圆有关的角
　　(1)圆心角：                   叫圆心角.
　　 　圆心角的性质：圆心角的度数等于它所对的弧的度数.
　　(2)圆周角：                         .
　　 　圆周角的性质：
　　 　①圆周角等于它所对的弧所对的圆心角的                   .
　　 　②同弧或等弧所对的                   ；在同圆或等圆中，相等的圆周角所对的       .
　　 　③90°的圆周角所对的弦为       ；半圆或直径所对的圆周角为       .
　　 　④如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.
　　 　⑤圆内接四边形的             ；外角等于它的       .
要点诠释：
　　(1)圆周角必须满足两个条件：①顶点在圆上；②角的两边都和圆相交.
　　(2)圆周角定理成立的前提条件是在同圆或等圆中.
知识点02  与圆有关的位置关系1．判定一个点P是否在⊙O上
　　设⊙O的半径为r，OP=d，则有
                   ；                   ；                   ；要点诠释：点和圆的位置关系和点到圆心的距离的数量关系是相对应的，即知道位置关系就可以确定数量关系；知道数量关系也可以确定位置关系.2．判定几个点在同一个圆上的方法
　　当时，在⊙O 上.
3．直线和圆的位置关系
　　设⊙O 半径为R，点O到直线l的距离为d.
　　(1)直线l和⊙O没有公共点直线和圆                            .(2)直线l和⊙O有唯一公共点直线和圆                        .(3)直线l和⊙O有2个公共点直线和圆                          .4．切线的判定、性质
　　(1)切线的判定：
　　 　①经过半径的外端并且       这条半径的直线是圆的切线.
　　 　②到圆心的距离d等于圆的半径的直线是圆的切线.
　　(2)切线的性质：
　　 　①圆的切线       过切点的       .
　　 　②经过圆心作圆的切线的垂线经过切点.
　　 　③经过切点作切线的垂线经过圆心.
　　(3)切线长：从圆外一点作圆的切线，这一点和切点之间的线段的长度叫做切线长.
　　(4)切线长定理：从圆外一点       ，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.
5．圆和圆的位置关系
　　设的半径为，圆心距.
(1)和没有公共点，且每一个圆上的所有点在另一个圆的                   ；(2)和没有公共点，且每一个圆上的所有点在另一个圆的                          ；(3)和有唯一公共点，除这个点外，每一个圆上的所有点在另一个圆的外部                   ；(4)和有唯一公共点，除这个点外，每一个圆上的所有点在另一个圆的内部                    ；(5)和有2个公共点                   ；知识点03  三角形的外接圆与内切圆、圆内接四边形与外切四边形1．三角形的内心、外心、重心、垂心
　　(1)三角形的内心：是三角形       的交点，它是三角形内切圆的圆心，在三角形内部，它到三角形三边的距离相等，通常用“I”表示.
　　(2)三角形的外心：是三角形       的交点，它是三角形外接圆的圆心，锐角三角形外心在三角形内部，直角三角形的外心是斜边中点，钝角三角形外心在三角形外部，三角形外心到三角形三个顶点的距离相等，通常用O表示.
　　(3)三角形重心：是三角形       的交点，在三角形内部；它到顶点的距离是到对边中点距离的  ，通常用G表示.
　　(4)垂心：是三角形       的交点.要点诠释：
　　(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；
　　(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).
　　(3) 三角形的外心与内心的区别：名称确定方法图形性质外心(三角形外接圆的圆心)三角形三边中垂线的交点(1)OA=OB=OC；(2)外心不一定在三角形内部内心(三角形内切圆的圆心)三角形三条角平分线的交点(1)到三角形三边距离相等；(2)OA、OB、OC分别平分∠BAC、∠ABC、∠ACB； (3)内心在三角形内部.2．圆内接四边形和外切四边形
　　(1)  的四边形叫圆的内接四边形，圆内接四边形        ，外角等于       .
　　(2)各边都和圆相切的四边形叫圆外切四边形，圆外切四边形       .知识点04  圆中有关计算1．圆中有关计算
　　圆的面积公式：         ，周长       .
　　圆心角为、半径为R的弧长       .
　　圆心角为，半径为R，弧长为l的扇形的面积        .
　　弓形的面积要转化为扇形和三角形的面积和、差来计算.
　　圆柱的侧面图是一个矩形，底面半径为R，母线长为l的圆柱的体积为          ，侧面积为，全面积为.
　　圆锥的侧面展开图为扇形，底面半径为R，母线长为l，高为h的圆锥的侧面积为，全面积为 ，母线长、圆锥高、底面圆的半径之间有       .要点诠释：
(1)对于扇形面积公式，关键要理解圆心角是1°的扇形面积是圆面积的，即            ；
(2)在扇形面积公式中，涉及三个量：扇形面积S、扇形半径R、扇形的圆心角，知道其中的两个量就可以求出第三个量.
(3)扇形面积公式S扇形，可根据题目条件灵活选择使用，它与三角形面积公式有点类似，可类比记忆；
(4)扇形两个面积公式之间的联系：S扇形            .
 考法01   圆的基础知识【典例1】如图，已知⊙O是以数轴的原点O为圆心，半径为1的圆，∠AOB=45°,点在数轴上运动，若过点P且与OA平行（或重合）的直线与⊙O有公共点, 设OP=x，则的取值范围是（     ）.A．－1≤≤1     B．≤≤    C．0≤≤     D．＞  【答案】B；【即学即练1】如图，已知⊙O是以数轴的原点为圆心，半径为1的圆，∠AOB=45°，点P在数轴上运动，若过点P且与OB平行的直线于⊙O有公共点，设P（x，0），则x的取值范围是（　　）.A．-1≤x＜0或0＜x≤1      B．0＜x≤1    C．-≤x＜0或0＜x≤    D．x＞1考法02   弧、弦、圆心角、圆周角的关系及垂径定理【典例2】如图所示，已知在⊙O中，AB是⊙O的直径，弦CG⊥AB于D，F是⊙O上的点，且，BF交CG于点E，求证：CE＝BE．   【即学即练2】如图所示，在⊙O内有折线OABC,其中OA=8,AB=12,∠A=∠B=60°,则BC的长为（    ）A．19    B．16 C．18  D．20考法03   圆中有关的计算【典例3】如图，AB是⊙O的直径，=，连接ED、BD，延长AE交BD的延长线于点M，过点D作⊙O的切线交AB的延长线于点C．（1）若OA=CD=2，求阴影部分的面积；（2）求证：DE=DM．【即学即练3】如图，⊙O是△ABC的外接圆，AB是⊙O的直径，FO⊥AB，垂足为点O，连接AF并延长交⊙O于点D，连接OD交BC于点E，∠B=30°，FO=2．（1）求AC的长度；（2）求图中阴影部分的面积．（计算结果保留根号）考法04   圆与其他知识的综合运用【典例4】如图，直径AB为6的半圆，绕A点逆时针旋转60°，此时点B到了点B′，则图中阴影部分的面积是（    ）. A. 3 B. 6      C. 5 D. 4                                      【即学即练4】某中学举办校园文化艺术节，小颖设计了同学们喜欢的图案“我的宝贝”，图案的一部分是以斜边长为12cm的等腰直角三角形的各边为直径作的半圆，如图所示，则图中阴影部分的面积为(    ).

　　A. 　　　B.72 　　　C.36 　　　D.72
 考法05  与圆的切线相关的证明与计算【典例5】如图，以△ABC的BC边上一点O为圆心的圆，经过A、B两点，且与BC边交于点E，D为BE的下半圆弧的中点，连接AD交BC于F，若AC=FC．（1）求证：AC是⊙O的切线：（2）若BF=8，DF=，求⊙O的半径；（3）若∠ADB=60°，BD=1，求阴影部分的面积．（结果保留根号）【即学即练5】如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．（1）求证：直线DE是⊙O的切线；（2）若⊙O半径为1，BC＝4，求图中阴影部分的面积．