2023年中考数学高频考点突破——一次函数与四边形综合

这是一份2023年中考数学高频考点突破——一次函数与四边形综合，共43页。试卷主要包含了已知等内容，欢迎下载使用。

2023年中考数学高频考点突破——一次函数与四边形综合
1．如图，已知四边形ABCD为矩形，O为坐标原点，点A的坐标为（0，6），点C的坐标为（8，0），点P是线段BC上一动点，已知点D是直线AE上位于第一象限的任意一点，直线AE与x轴交于点E（﹣3，0）；
（1）求直线AE的关系式；
（2）连接PD，当AD＝AP、∠DAP＝90°时，求图象经过点D的反比例函数的关系式；
（3）若将直线AD向右平移6个单位后，在该直线上是否存在一点D，使△APD成为等腰直角三角形？若存在，请直接写出点D的坐标，若不存在，请说明理由．

2．如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48＝0的两个实数根．
（1）求直线MN的函数关系式；
（2）点P从O出发，以每秒1个单位的速度沿x的正半轴匀速运动，运动时间为t，△ABP面积为S，求S与t的函数关系；
（3）在（2）的条件下，当t＝4秒时，在平面内是否存在一点Q，使得以A，C，P，Q为顶点的四边形是平行四边形？若存在，请求出点Q的坐标；若不存在，请说明理由．




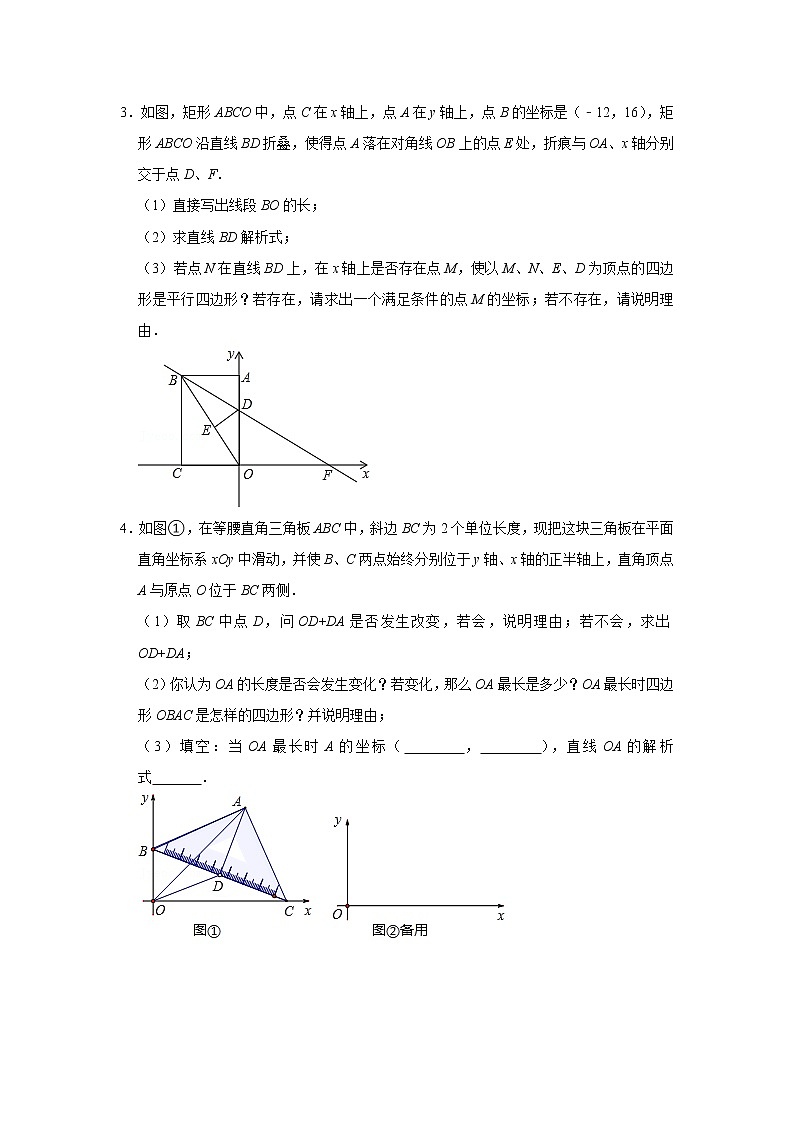
3．如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（﹣12，16），矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F．
（1）直接写出线段BO的长；
（2）求直线BD解析式；
（3）若点N在直线BD上，在x轴上是否存在点M，使以M、N、E、D为顶点的四边形是平行四边形？若存在，请求出一个满足条件的点M的坐标；若不存在，请说明理由．

4．如图①，在等腰直角三角板ABC中，斜边BC为2个单位长度，现把这块三角板在平面直角坐标系xOy中滑动，并使B、C两点始终分别位于y轴、x轴的正半轴上，直角顶点A与原点O位于BC两侧．
（1）取BC中点D，问OD+DA是否发生改变，若会，说明理由；若不会，求出OD+DA；
（2）你认为OA的长度是否会发生变化？若变化，那么OA最长是多少？OA最长时四边形OBAC是怎样的四边形？并说明理由；
（3）填空：当OA最长时A的坐标（　 　，　 　），直线OA的解析式　 　．







5．如图，矩形OABC在坐标系中，OA＞OC，矩形面积为12，对角线AC的长为5．
（1）求A，C的坐标；
（2）若D为AC中点，过D的直线交y轴负半轴于E，交BC于F，且OE＝1，求直线EF的解析式；
（3）在（2）的条件下，在坐标平面内是否存在一点G，使以C，D，F，G为顶点的四边形为平行四边形？若存在，请直接写出点G的坐标；若不存在，请说明理由．

6．如图，一次函数y＝﹣x+1的图象与x轴、y轴分别交于点A、B，以线段AB为边在第一象限内作等边△ABC，
（1）求△ABC的面积；
（2）如果在第二象限内有一点P（a，），试求四边形AOPB的面积S与a之间的函数关系式，并求出当△ABP的面积与△ABC的面积相等时a的值；
（3）在x轴上，是否存在这样的点M，使△MAB为等腰三角形？若存在，请写出所有符合要求的点M的坐标，并说明理由．






7．已知：如图平面直角坐标系xOy中，C在x轴上，四边形OABC为菱形，且A点坐标
为（﹣3，4），过A、C的直线交y轴于点M，连接BM
（1）求直线AC的解析式
（2）一动点P从A出发，以每秒2个单位长度沿A→B→C向C点运动，设运动过程中△PBM的面积为S，运动时间为t（秒），试求出S关于t的函数关系式．
（3）在（2）的条件下，试求出当t为何值时，△PBM的面积的最大值？最大值是多少？

8．如图，直线AB与两坐标轴分别相交于A、B两点，A（4，0），B（0，4），点M是线段AB上任意一点（A、B点除外）过M分别作MC⊥OA于点C，MD⊥OB于D．
（1）当点M在AB上运动时，你认为四边形OCMD的周长是否发生变化，并说明理由．
（2）设MC＝x，用含x的代数式表示长方形OCMD的面积，并求出当点M运动到什么位置时，长方形OCMD的面积有最大值？最大值是多少？
（3）当长方形OCMD为正方形时，将正方形OCMD沿着x轴的正方向移动，设平移的距离为a（0＜a＜4），在平移过程中正方形OCMD始终被线段AB分割成两个图形．当a为何值时正方形OCMD被线段分割形成的三角形的面积是1？







9．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴y轴的正半轴上，OA＝3，OB＝4，D为OB的中点，点E为边OA上的一个动点．
（1）求线段CD所在直线的解析式；
（2）当△CDE的周长最小时，求此时点E的坐标；
（3）当点E为OA中点时，坐标平面内，是否存在点F，使以D、E、C、F为顶点的四边形是平行四边形？若存在，请直接写出F点的坐标；若不存在，请说明理由．

10．如图，在平面直角坐标系中，以点A坐标为（6，0），点B坐标为（0，8），动点P从点A开始沿折线AO﹣OB﹣BA运动，点P在AO，OB，BA边上运动的速度分别为每秒3，4，5个单位，直线l从与OA重合的位置开始，以每秒个单位的速度沿OB方向平行移动，即移动过程中保持l∥OA，且分别与OB，AB边交于E，F两点，同时出发，设运动时间为t秒，当点P与点F相遇时，点P和直线l同时停止运动．
（1）线段AB所在直线的表达式为　 　；点F横坐标为　 　（用t的代数式表示）；
（2）设△APE的面积为S（S≠0），请求出点P和直线l运动过程中S与t的函数关系式；
（3）在点P和直线l运动过程中，作点P关于直线l的对称点，记为点Q，若形成四边形PEQF是菱形，请直接写出t的值．



11．如图，在直角坐标系中，矩形ABCO的边OC与x轴重合，OA与y轴重合，BC＝4，D是OC上一点，且OD，DC的长是一元二次方程x2﹣10x+16＝0的两个根（OD＞DC）．
（1）求直线BD的函数解析式；
（2）在AB上有一动点P（不与A、B重合）自A点沿AB方向向B匀速运动，运动速度为每秒1个单位长度，设运动的时间为t秒，过P点作PE∥BD交AD于E，过P点作PF∥AD交BD于F，求四边形DEPF的面积s与时间t的函数关系式；
（3）在（2）的条件下是否存在一点P，以A、P、D为顶点的三角形为等腰三角形？若存在，请直接写出相应点P的坐标；若不存在请说明理由．

12．如图，四边形ABCD是矩形，点P是直线AD与BC外的任意一点，连接PA、PB、PC、PD．请解答下列问题：

（1）如图1，当点P在线段BC的垂直平分线MN上（对角线AC与BD的交点Q除外）时，证明△PAC≌△PDB；
（2）如图2，当点P在矩形ABCD内部时，求证：PA2+PC2＝PB2+PD2；
（3）若矩形ABCD在平面直角坐标系xOy中，点B的坐标为（1，1），点D的坐标为（5，3），如图3所示，设△PBC的面积为y，△PAD的面积为x，求y与x之间的函数关系式．



13．如图1，在直角坐标系中，点B（a，b）在第一象限，且+b2﹣8b+16＝0，过B作x轴，y轴的垂线分别交于A、C．

（1）求B的坐标和四边形OABC的面积．
（2）直线y＝2x+8交x轴于E，交y轴于F，它沿x轴正方向以每秒移动1个单位的速度，设平移的时间为t秒，问是否存在t的值，使直线EF平分四边形OABC的面积？若存在，求t的值；若不存在，说明理由．
（3）如图2，P为正方形OABC的多角线AC上的点（端点A，C除外），PM⊥PO，交直线AB于M，问的值是否不变？请给出结论，予以证明并求其值．
14．如图，在平面直角坐标系xOy中，直线y＝﹣x+与x轴、y轴分别相交于点A、C，将Rt△OAC折叠，使OC边落在AC边上，点O与点D重合，折痕为CE．
（1）求折痕CE的解析式；
（2）求点D的坐标；
（3）设点M为直线CE上的一点，过点M作AC的平行线，交y轴于点N，是否存在这样的点M，使得以M、N、D、C为顶点的四边形是平行四边形？若存在，请求出符合条件的点M的坐标；若不存在，请说明理由．



15．如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2﹣7x+12＝0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒．
（1）求A、B两点的坐标．
（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标．
（3）当t＝2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．

16．将▱OABC放置在平面直角坐标系xOy内，已知AB边所在直线的函数解析式为：y＝﹣x+4．若将▱OABC绕点O逆时针旋转90°得OBDE，BD交OC于点P．
（1）直接写出点C的坐标是　 　：
（2）求△OBP的面积；
（3）若再将四边形OBDE沿y轴正方向平移，设平移的距离为x（0≤x≤8），与▱OABC重叠部分周长为L，试求出L关于x的函数关系式．






17．在平面直角坐标系中，直线y＝﹣x+6与x轴、y轴分别交于点B、A，点D、E分别是AO、AB的中点，连接DE，点P从点D出发，沿DE方向匀速运动，速度为1cm/s；与此同时，点Q从点B出发，沿BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（s）（0＜t＜4）．解答下列问题：
（1）分别写出点P和Q坐标（用含t的代数式表示）；
（2）①当点Q在BE之间运动时，设五边形PQBOD的面积为y（cm2），
求y与t之间的函数关系式；
②在①的情况下，是否存在某一时刻t，使PQ分四边形BODE两部分的面积之比为S△PQE：S五边形PQBOD＝1：29？若存在，求出此时t的值；若不存在，请说明理由；
（3）以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，当t为何值时，⊙P能与△ABO的一边相切？

18．如图，平面直角坐标系中，直线l分别交x轴、y轴于A、B两点（OA＜OB）且OA、OB的长分别是一元二次方程x2﹣（+1）x+＝0的两个根，点C在x轴负半轴上，且AB：AC＝1：2
（1）求A、C两点的坐标；
（2）若点M从C点出发，以每秒1个单位的速度沿射线CB运动，连接AM，设△ABM的面积为S，点M的运动时间为t，写出S关于t的函数关系式，并写出自变量的取值范围；
（3）点P是y轴上的点，在坐标平面内是否存在点Q，使以 A、B、P、Q为顶点的四边形是菱形？若存在，请直接写出Q点的坐标；若不存在，请说明理由．



19．如图，直线y＝﹣x+4与坐标轴分别交于点A、B，与直线y＝x交于点C．在线段OA上，动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动，同时动点P从点A出发向点O做匀速运动，当点P、Q其中一点停止运动时，另一点也停止运动．分别过点P、Q作x轴的垂线，交直线AB、OC于点E、F，连接EF．若运动时间为t秒，在运动过程中四边形PEFQ总为矩形（点P、Q重合除外）．
（1）求点P运动的速度是多少？
（2）当t为多少秒时，矩形PEFQ为正方形？
（3）当t为多少秒时，矩形PEFQ的面积S最大？并求出最大值．

20．如图1，在平面直角坐标系中，AB⊥x轴正半轴于点A，连接OB，B（2，8），AD是∠BAO外角的角平分线，过点B作BD⊥AD于点D．

（1）求点D的坐标；
（2）如图2，动点P，从B点出发，沿BA以2个单位的速度向A运动，PQ∥BD交AD于点Q，交y轴于点G，设四边形OAQG的面积为S，运动时间为t，请用t表示S的关系式；
（3）在（2）的条件下，当t为何值时，Rt△OAP的两直角边的比为2：1；并求此时直线PQ与x轴交点M的坐标．

参考答案：
1．【解答】解：（1）设直线AE：y＝k1x+b，
∵点A（0，6），E（﹣3，0）在直线AE上，
∴，
∴，
∴直线AE的解析式是：y＝2x+6，
（2）如图1所示，作DT⊥y轴于T点，作PF⊥y轴于F点，可得∠DEA＝∠AFP＝90°，
∵△DAP为等腰直角三角形，
∴AD＝AP，∠DAP＝90°，
∴∠TAD+∠DAB＝90°，∠DAB+∠BAP＝90°，
∴∠TAD＝∠BAP，
∵AB∥PF，
∴∠BAP＝∠FPA，
∴∠TAD＝∠FPA，
∴△ADT≌△PAF（AAS），
∴AT＝PF＝8，OT＝OA+AT＝14，
设点D的横坐标为x，由14＝2x+6，得x＝4，
∴点D的坐标是（4，14）；
设过点D的反比例函数的关系式为：，则k2＝14×4＝56，
∴反比例函数的关系式为：；
（3）存在点D，使△APD是等腰直角三角形，理由为：
直线y＝2x+6向右平移6个单位后的解析式为y＝2（x﹣6）+6＝2x﹣6，
如图2所示，当∠ADP＝90°时，AD＝PD，易得D点坐标（4，2）；
如图3所示，当∠APD＝90°时，AP＝PD，设点P的坐标为（8，m），
则D点坐标为（14﹣m，m+8），由m+8＝2（14﹣m）﹣6，得m＝，
∴D点坐标（，）；
如图4所示，当∠ADP＝90°时，AD＝PD时，同理可求得D点坐标（，），
综上，符合条件的点D存在，坐标分别为（4，2），（，），（，）．


2．【解答】解：（1）解方程x2﹣14x+48＝0得：x1＝6，x2＝8，
则OA＝8，OC＝6，A的坐标是（8，0），C的坐标是（0，6）．
设直线MN的解析式是y＝kx+b，
根据题意得：，
解得：，
则直线MN的解析式是：y＝﹣x+6；
（2）当P在线段OA上时，即0≤t≤8时，AP＝8﹣t，
则S＝×（8﹣t）×6＝24﹣3t，
当t＞8时，AP＝t﹣8，则S＝×（t﹣8）×6＝3t﹣24；
（3）当t＝4秒时，P的坐标是（4，0），
则当是平行四边形ACQP时，CQ∥x轴，且CQ＝AP＝4，则Q的坐标是（﹣4，6）；
当是平行四边形APCQ时，CQ∥AP且CQ＝AP，则Q的坐标是（4，6）；
当是平行四边形PQAC时，AP的中点是（6，0），Q的纵坐标是﹣6，设横坐标是m，则＝6，
解得：m＝12，
则Q的坐标是（12，﹣6）．

3．【解答】解：（1）20；
（2）∵矩形ABCO中点B的坐标是（﹣12，16），
∴AB＝12，OA＝16，
设D（0，a）则OD＝a，AD＝ED＝16﹣a，
在Rt△AOB与Rt△EOD中，∠AOB＝∠EOD，∠OAB＝∠OED＝90°，
∴△OED∽△OAB，
∴＝，即＝，
解得：a＝10，
∴D（0，10），
设直线DB的解析式y＝kx+b经过B（﹣12，16），D（0，10），
∴有，解得，
∴直线BD的解析式为：y＝﹣x+10，

（3）如图2，当M在F的左边时，
作EG⊥x轴于G，作EM∥BD交轴与M，MN∥ED交BF于N，
∴四边形DEMN是平行四边形，
∵EG⊥x轴，BC⊥x轴，
∴EG∥BC，
∴＝＝，
∵OB＝20，BE＝12，BC＝16，OC＝12，
∴OE＝8，
即＝＝，
∴EG＝6.4，OG＝4.8，
∴E（﹣4.8，6.4），
∵直线BD的解析式为：y＝﹣x+10，
∴设直线EM的解析式为：y＝﹣x+b，
把E（﹣4.8，6.4）代入得6.4＝﹣×（﹣4.8）+b，
解得；b＝4，
∴直线EM的解析式y＝﹣x+4，
令y＝0，则﹣x+4＝0，解得x＝8，
∴M（8，0），
当点M在点F的右边时，
∵直线BD的解析式为：y＝﹣x+10，
∴F（20，0），
∵M′与M关于F点对称，
∴M′（32，0），
综上，M点的坐标为（8，0）或（32，0）．
4．【解答】解：（1）OD＝BC＝2×＝1，则OD+DA＝2．

（2）∵OD＝DA＝1始终不变，
∴当O、D、A三点在一直线上时，OA最长等于2．
这时，四边形OBAC的对角线相交于点D，有DO＝DB＝DA＝DC＝1，OA＝BC＝2，
∵四边形OBAC是矩形，
又∵AB＝AC，
∴四边形OBAC是正方形．

（3）A（，）
直线OA是∠BOC的角平分线，则解析式是：y＝x．
5．【解答】解：（1）由矩形的面积公式可知：OA•OC＝12，
在Rt△COA中由勾股定理得：OA2+OC2＝5．
解得：AO＝4，OC＝3．
∴点A的坐标为（4，0），点C的坐标为（0，3）．
（2）∵点D为AC的中点，
∴点D的坐标为（2，1.5）．
∵OE＝1，
∴点E的坐标为（0，﹣1）．
设直线EF的解析式为y＝kx+b，将点D和点E的坐标代入得：
解得：．
∴直线EF的解析式为y＝﹣1．
（3存在．
理由：∵点F在BC上，
∴点F的纵坐标为3．
将y＝3代入y＝﹣1得：﹣1＝3．
解得：x＝．
∴点F的坐标为（，3）．
①如图1所示；

∵四边CDFG为平行四边形，
∴GM＝MD，CM＝MF．
∴点M的坐标为（，3）．
设点G的坐标为（x，y）．
∴，．
解得：x＝，y＝4.5．
∴点G的坐标为（，）．
②如图2所示；

∵点F的坐标为（，3）．
∴CF＝．
∵四边形CGDF为平行四边形，
∴CF∥GD，CF＝DG．
∴点G的坐标为（﹣，）．
③如图3所示

∵四边形CDGF为平行四边形，
∴CF∥GD，CF＝DG．
∴点G的坐标为（，）．
综上所述，点G的坐标为（，）或（，）或（，）．
6．【解答】解：（1）如图1，过点C作CD⊥AB，
当x＝0，y＝1；当y＝0，则x＝，则A（，0），B（0，1），
AB＝＝2，
过C作CD⊥AB于D，
∵△ABC是等边三角形，∴BD＝AB＝×2＝1，
∴CD＝BD•tan60°＝1×＝．
∴S△ABC＝AB•CD＝×2×＝；

（2）如图2，过点P作PM⊥y轴，PN⊥x轴，交y轴上一点M，x轴上一点N，
∵A（，0），B（0，1），P（a，），
∴S△AOB＝××1＝，S△AOP＝××＝，S△BOP＝|a|•OB＝﹣，
∴S四边形ABPO＝S△AOB+S△BOP＝
∵S△ABP＝S四边形ABPO﹣S△APO，
∴当△ABP的面积与△ABC的面积相等时，﹣＝，
解得：a＝﹣；

（3）如图3，∵△MAB为等腰三角形，A（，0），
∴M1（﹣，0）；
∵AB＝＝2，
∴AM2＝2，
∴M2（﹣2，0）；
同理可得：M3（，0），M4（+2，O）；
则满足条件的点M有4个，M1（﹣，0）．M2（﹣2，0），M3（，0），M4（+2，O）；



7．【解答】解：（1）如图1，作AD⊥x轴于D点．
，
由勾股定理，得
AO＝＝＝5，
由菱形的定义，得OC＝AO＝AB＝5，
C（5，0）．
设AC的解析式为y＝kx+b，图象过A、C点，
，
解得，
直线AC的解析式y＝﹣x+；
（2）①当0≤t时，如图2：
，
AC与y轴的交点坐标（0，），
MD＝OD﹣OM＝4﹣＝．
AP＝2t，PB＝5﹣2t．
S＝PB•MD，即S＝××（5﹣2t），
化简，得S＝﹣t；
②当＜t≤5时，作ME⊥BC于E点，如图3：
，
S△ABC＝SAOCB＝OC•OD＝10．
S△ABC＝S△ABM+S△BCM＝×5×+×5ME＝10．
解得ME＝．
S＝PB•ME，及S＝×（2t﹣5），
化简，得S＝t﹣，
综上所述：S＝；
（3）①当0≤t＜时，S随t的增大而减小，当t＝0时，S最大＝，
②当＜t≤5时，s随t的增大而增大，当t＝5时，S最大＝，
综上所述：当t＝5时，S最大＝．
8．【解答】解：（1）设点M的横坐标为x，则点M的纵坐标为﹣x+4（0＜x＜4，﹣x+4＞0），
则：MC＝|﹣x+4|＝﹣x+4，MD＝|x|＝x，
∴C四边形OCMD＝2（MC+MD）＝2（﹣x+4+x）＝8，
∴当点M在AB上运动时，四边形OCMD的周长不发生变化，总是等于8．
（2）根据题意得：S四边形OCMD＝MC•MD＝（﹣x+4）•x＝﹣x2+4x＝﹣（x﹣2）2+4，
∴四边形OCMD的面积是关于点M的横坐标x（0＜x＜4）的二次函数，并且当x＝2，S有最大值4，
此时M是AB的中点，
即当点M运动到线段AB的中点时，四边形OCMD的面积最大且最大面积为4．
（3）①当0＜a≤2时，如图（2），

MH＝a，
∵A（4，0），B（0，4），
∴OA＝OB＝4，
∴∠OAB＝∠OBA＝45°，
∴∠CKA＝45°，
∵∠MKH＝∠CKA，
∴∠MKH＝∠OAB＝45°，
∴MK＝NH＝a，
∴a2＝1，
∴a＝±，
a＝﹣（舍去），
∴a＝；
②如图（3），

当2＜a≤4时，OO′＝a，O′A＝4﹣a，
∵∠OAB＝45°，
∴∠O′HA＝45°，
∴OH＝O′A＝4﹣a，
∴，
解得：a＝4±，
经检验a＝4＞4，不合题意，舍去，
∴a＝4﹣，
综上所述，当a＝或a＝4﹣时，正方形OCMD被线段分割形成的三角形的面积是1．
9．【解答】解：（1）∵四边形OACB是矩形，
∴AC＝OB＝4，∠OBC＝90°，
∵D为OB的中点，
∴OD＝BD＝2，
∴C（3，4），D（0，2），
设线段CD所在直线的解析式为y＝kx+b，
代入C（3，0），D（0，2）得：，
解得：k＝，b＝2，
∴线段CD所在直线的解析式为：y＝x+2；
（2）当△CDE的周长最小时，DE+CE最小；
作点D关于OA的对称点D′，连接CD′交OA于E，如图1所示：
则D′（0，﹣2），DE＝DE′，
∴DE+CE＝D′E+CE＝CD′，
∵∠OBC＝90°，BD′＝6，
∵AC∥OB，
∴△OED′∽△AEC，
∴＝＝，
∴AE＝2AE，
∵OA＝3，
∴OE＝1，
∴E（1，0）；
（3）存在；分三种情况：
①CE为对角线时，作FM⊥x轴于M；如图2所示：
∵BC∥OA，
∴∠MEC＝∠BCE，
∵四边形DEFC是平行四边形，
∴CD∥EF，
∴∠FEC＝∠DCE，
∴∠MEF＝∠BCD，
在△EMF和△CBD中，
，
∴△EMF≌△CBD（AAS），
∴OM＝BC＝3，FM＝DB＝2，
∴OM＝1.5+3＝4.5，
∴F（4.5，2）；
②DE为对角线时，作F1N⊥x轴于N，则 F1N∥FM，如图2所示：
∵EF1＝CD＝EF1，
∴NE＝ME＝3，NF1＝FM＝2，
∴ON＝1.5，
∴F1（﹣1.5，﹣2）；
③DC为对角线时，作F1Q⊥y轴于Q，作F2P⊥y轴于P，如图所示：
同②得：PF2＝F1Q＝ON＝1.5，PD＝DQ＝4，
∴OP＝6，
∴F2（1.5，6）；
综上所述：F点的坐标为（4.5，2），或（1.5，6），或（﹣1.5，﹣2）．


10．【解答】解：（1）设直线AB的解析式是y＝kx+b，根据题意得：，
解得：，
则直线AB的解析式是：y＝﹣x+8．
在解析式中，令y＝t，则﹣x+8＝t，
解得：x＝6﹣t；

（2）当0＜t≤2时（如图1），P在OA上，OA＝3t，E的坐标是（0，t），则S＝×3t•t＝2t2；
当t＝4（t﹣2），解得：t＝3，
则2＜t＜3时，P和E都在OB上，且P在E的下边，则PE＝t﹣4（t﹣2）＝8﹣t，
则S＝（8﹣t）×6＝24﹣8t；
当3＜t＜4时，P和E都在OB上，且P在E的上边，且PE＝4（t﹣2）﹣t＝t﹣8，
则S＝（t﹣8）×6＝8t﹣24；
当t＞4时，当P在BA上时（如图2），则BP＝5（t﹣4），作PM⊥y轴于点M．
则△BPM∽△BAO，
＝，
即＝＝，
解得：PM＝3t﹣12，BM＝4t﹣16．
当t＝8﹣（4t﹣16）时，t＝，即当t＝时，P和F重合，点P和直线l同时停止运动．
当4≤t≤时，S△AOE＝OE•OA＝×t×6＝4t，S△BEP＝×（8﹣t）×（3t﹣12）＝﹣2t2+20t﹣48，S△OAB＝×6×8＝24，
则S＝24﹣4t﹣（﹣2t2+20t﹣48）＝2t2﹣24t+72；

（3）当P在OA上时，当P在EF的中垂线上时，能构成菱形，此时OP＝EF，即6﹣3t＝（6﹣t），解得：t＝；
当P在P在线段OB上时，形成的是三角形，不存在菱形；
当P在AB上时（如图2），PM＝EF时，即3t﹣12＝（6﹣t），解得：t＝．


11．【解答】解：（1）解x2﹣10x+16＝0，得x＝2或x＝8，
由题意可得：D（8，0），C（10，0），B（10，4），
设直线BD的解析式为：y＝kx+b，
∴ 解得：
∴直线BD的解析式为：y＝2x﹣16；

（2）∵AB＝OC＝10，OA＝BC＝4，OD＝8，DC＝2，
∴S△ADB＝S矩形﹣S△OAD﹣S△BDC＝4×10﹣×4×8﹣×2×4＝20，
∵PE∥BD，
∴＝（）2＝（）2＝，
∴S△AEP＝×20＝，
同理S△BPF＝×20＝，
∴S＝S△ADB﹣S△AEP﹣S△AEP＝20﹣﹣＝﹣t2+4t；
即S＝﹣t2+4t；

（3）设P（t，4），
∴PD2＝（8﹣t）2+42，
当PD＝AP时，则t2＝（8﹣t）2+42，解得：t＝5，
∴P（5，4）；
当AP＝AD时，则t＝＝＝4；
∴P（4，4）
∴以A、P、D为顶点的三角形为等腰三角形时，P的坐标为（5，4）或（4，4）．
12．【解答】解：（1）作BC的中垂线MN，在MN上取点P，连接PA、PB、PC、PD，
如图（1）所示，∵MN是BC的中垂线，
∴PA＝PD，PC＝PB，
又∵四边形ABCD是矩形，
∴AC＝DB，
即，
∴△PAC≌△PDB（SSS），

（2）证明：过点P作KG∥BC，如图（2）
∵四边形ABCD是矩形，
∴AB⊥BC，DC⊥BC
∴AB⊥KG，DC⊥KG，
∴在Rt△PAK中，PA2＝AK2+PK2
同理，PC2＝CG2+PG2；PB2＝BK2+PK2，PD2＝DG2+PG2
PA2+PC2＝AK2+PK2+CG2+PG2，PB2+PD2＝BK2+PK2+DG2+PG2
AB⊥KG，DC⊥KG，AD⊥AB，可证得四边形ADGK是矩形，
∴AK＝DG，同理CG＝BK，
∴AK2＝DG2，CG2＝BK2
∴PA2+PC2＝PB2+PD2

（3）∵点B的坐标为（1，1），点D的坐标为（5，3）
∴BC＝4，AB＝2，
∴S矩形ABCD＝4×2＝8，
直线HI垂直BC于点I，交AD于点H，
当点P在直线AD与BC之间时，
S△PAD+S△PBC＝BC•HI＝4，
即x+y＝4，因而y与x的函数关系式为y＝﹣x+4，
当点P在直线AD上方时，S△PBC﹣S△PAD＝BC•HI＝4，
而y与x的函数关系式为y＝4+x，
当点P在直线BC下方时，S△PAD﹣S△PBC＝BC•HI＝4，
y与x的函数关系式为y＝x﹣4．

13．【解答】解：（1）∵且+b2﹣8b+16＝+（b﹣4）2＝0，
∴a﹣4＝0，且b﹣4＝0，
即a＝4，b＝4．
点B的坐标为（4，4）．
∴OA＝AB＝BC＝CO＝4，
∴四边形OABC的面积S＝OA•AB＝4×4＝16．
（2）当y＝0时，x＝﹣4，
∴E点的坐标为（﹣4，0）．
当直线EF平移到过D点时正好平分正方形AOBC的面积．
设平移后的直线为y＝2x+b，代入D点坐标，求得b＝﹣2．
此时直线和x轴的交点坐标为（1，0），平移的距离为5，所以t＝5秒．
（3）过P点作NQ∥OA，GH∥CO，交CO、AB于N、Q，交CB、OA于G、H，
在△OPH与△MPQ中，
，
∴△OPH≌△MPQ，四边形CNPG为正方形．
∴PG＝BQ＝CN．
∴，即．

14．【解答】解：（1）由题意知∠CAO＝30°，
∴∠OCE＝∠ECD＝∠OCA＝30°，
∵直线y＝﹣x+与x轴、y轴分别相交于点A、C，
∴C（0，），
∴在Rt△COE中，OE＝OC•tan∠OCE＝×＝1，
∴点E的坐标是（1，0），
设直线CE的解析式为y＝kx+b．
把点C（0，），E（1，0）代入得，
解得．
∴直线CE的解析式为y＝﹣x+；
（2）在Rt△AOC中，AC＝＝2，
AO＝＝3，
∵CD＝OC＝，
∴AD＝AC﹣CD＝2﹣＝，
过点D作DF⊥OA于点F，
在Rt△AFD中，DF＝AD•sin∠CAO＝，
AF＝AD•cos∠CAO＝，
∴OF＝AO﹣AF＝，
∴点D的坐标是（，）．

（3）存在两个符合条件的M点，第一种情况：此点在第四象限内，设为M1，延长DF交直线CE于M1，
连接M1O，M1O∥AC，
则有DM1∥y轴，
∵OF＝，
∴设点M1的坐标为（，y1），
又∵点M1在直线CE上，
∴将点M1的坐标代入y＝﹣x+中，
得y1＝﹣×+＝﹣，即FM1＝．
∴点M1的坐标是（，﹣），
又∵DM1＝DF+FM1＝+＝，OC＝，
∴DM1＝OC，
又∵DM1∥OC，
∴四边形CDM1O为平行四边形，
又∵点O在y轴上，
∴点M1是符合条件的点．
第二种情况：此点在第二象限内，设为M2，
过点D作DN∥CE交y轴于N，过N点作NM2∥CD交直线CE于点M2，
则四边形M2N2DC为平行四边形，
∴M2N＝CD＝，
∵M2N∥CD，DN∥CE，
∴∠NM2C＝∠ACE，∠OCE＝∠M2CN，
∴CN＝M2N，
∵M2N＝CD＝，
∴CN＝，
作M2H⊥y轴于点H，
∵M2N∥CD，
∴∠M2NC＝∠NCD，
∴∠M2NH＝∠OCA＝60°，
在Rt△M2NH中，
M2H＝M2N•sin60°＝×＝，
NH＝M2N•cos60°＝×＝，
∴HO＝HN+CN+OC＝，
∴M2（﹣，），
∴点M2是符合条件的点，
综上所述，符合条件的两个点的坐标分别为M1（，﹣），M2（﹣，）．

15．【解答】解：（1）解方程x2﹣7x+12＝0，得x1＝3，x2＝4，
∵OA＜OB，∴OA＝3，OB＝4，
∴A（0，3），B（4，0）；
（2）在Rt△AOB中，OA＝3，OB＝4，∴AB＝5，∴AP＝t，QB＝2t，AQ＝5﹣2t．
△APQ与△AOB相似，可能有两种情况：
①△APQ∽△AOB，如图（1）所示．

则有＝，即＝，解得t＝．
此时OP＝OA﹣AP＝，PQ＝AP•tanA＝，
∴Q（，）；
②△APQ∽△ABO，如图（2）所示．

则有＝，即＝，解得t＝．
此时AQ＝，AH＝AQ•cosA＝，HQ＝AQ•sinA＝，OH＝OA﹣AH＝，
∴Q（，）．
综上所述，当t＝秒或t＝秒时，△APQ与△AOB相似，
所对应的Q点坐标分别为（，）或（，）；
（3）结论：存在．如图（3）所示．

∵t＝2，∴AP＝2，AQ＝1，OP＝1．
过Q点作QE⊥y轴于点E，则QE＝AQ•sin∠QAP＝，AE＝AQ•cos∠QAP＝，
∴OE＝OA﹣AE＝，
∴Q（，）．
∵▱APQM1，∴QM1⊥x轴，且QM1＝AP＝2，∴M1（，）；
∵▱APQM2，∴QM2⊥x轴，且QM2＝AP＝2，∴M2（，）；
如图（3），过M3点作M3F⊥y轴于点F，
∵▱AQPM3，∴M3P＝AQ，∠QAE＝∠M3PF，∴∠PM3F＝∠AQE；
在△M3PF与△QAE中，
，
∴△M3PF≌△QAE（ASA），
∴M3F＝QE＝，PF＝AE＝，∴OF＝OP+PF＝，∴M3（﹣，）．
∴当t＝2时，在坐标平面内，存在点M，使以A、P、Q、M为顶点的四边形是平行四边形，
点M的坐标为：M1（，）或M2（，）或M3（﹣，）．
16．【解答】解：（1）∵AB边所在直线的解析为：y＝﹣x+4，
∴点A的坐标为：（4，0），点B的坐标为：（0，4），
∵四边形ABCD是平行四边形，
∴BC＝OA＝4，BC∥OA，
∴点C的坐标为：（﹣4，4）；
故答案为：（﹣4，4）；
（2）由旋转的性质，可得：OD＝OB＝4，
∵∠BOD＝90°，
∴∠OBD＝45°，
∵OB＝BC，∠OBC＝90°，
∴∠BOC＝45°，
∴∠OPB＝90°，BP＝OP，
∵OB＝4，
∴OP＝BP＝2，
∴S△OBP＝OP•BP＝4；

（3）分两种情况考虑：
①当0≤x≤4时，如图1所示，可得△CPH，△HBG与△FKO都为等腰直角三角形，
∴GB＝OF，PH＝PC，KF＝OK，
此时重合部分五边形PHBFK的周长L＝BH+HP+PK+KF+BF＝GB+CP+PK+KO+BF＝OC+FG＝OC+OB＝4+4；
②当4≤x≤8时，如图2所示，此时△CPH与△BHF都为等腰直角三角形，
∴FB＝HB＝BG﹣GF＝x﹣4，CH＝CB﹣HB＝4﹣（x﹣4）＝8﹣x，CP＝PH＝（8﹣x），
此时重合部分△CHP的周长L＝CH+CP+PH＝8﹣x+2×（8﹣x）＝8+8﹣x﹣x，
综上，L＝．
17．【解答】（1）∵直线y＝﹣x+6与x轴、y轴分别交于点B、A，
∴点A的坐标为（0，6）
∵点D、E分别是AO、AB的中点，
∴DE∥x轴，
∴OD＝3，
∵点P从点D出发，沿DE方向匀速运动，速度为1cm/s；
∴P（t，3），Q（8﹣t，t）；

（2）①如图1，由P作PH⊥AB
△PHE∽△AOB∴
∴
S△PEQ
S四边形DOBE＝×3＝18
②×18
解得t＝﹣（舍），t＝2

（3）当⊙P与OB相切时，
分别过点P、Q作PF、QG垂直于x轴，垂足为F、G，
再过点Q作QH⊥PF于点H，
如图2构造直角△PHQ，
此时，△BQG∽△BAO，BQ＝2t，
得QG＝HF＝t，BG＝t，
在Rt△PHQ中，PH2+HQ2＝PQ2，
得（3﹣t）2+（8﹣t﹣t）2＝32，
解得：t1＝4（舍），t2＝
当⊙P与OA相切时，
分别过点P、Q作PF、QG垂直于x轴，垂足为F、G，
再过点Q作QH⊥PF于点H，
如图3构造直角△PHQ，
此时，△BQG∽△BAO，BQ＝2t，
得QG＝HF＝t，BG＝t，
在Rt△PHQ中，PH2+HQ2＝PQ2，
得（3﹣t）2+（8﹣t﹣t）2＝t2，
解得：t1＝＞4（舍），t2＝
当⊙P与AB相切时，如图4，
此时，PE＝4﹣t，EQ＝2t﹣5，
由△EPQ∽△BAO，得＝，
∴＝，
解得：t＝
∴当t＝，，时，⊙P可与△ABC的一边相切．


18．【解答】解：（1）x2﹣（+1）x+＝0，
（x﹣）（x﹣1）＝0，
解得x1＝，x2＝1，
∵OA＜OB，
∴OA＝1，OB＝，
∴A（1，0），B（0，），
∴AB＝2，
又∵AB：AC＝1：2，
∴AC＝4，
∴C（﹣3，0）；

（2）∵AB＝2，AC＝4，BC＝2，
∴AB2+BC2＝AC2，
即∠ABC＝90°，
由题意得：CM＝t，CB＝2．
①当点M在CB边上时，S＝2﹣t（0≤t）；
②当点M在CB边的延长线上时，S＝t﹣2（t＞2）；

（3）存在．
①当AB是菱形的边时，如图所示，
在菱形AP1Q1B中，Q1O＝AO＝1，所以Q1点的坐标为（﹣1，0），
在菱形ABP2Q2中，AQ2＝AB＝2，所以Q2点的坐标为（1，2），
在菱形ABP3Q3中，AQ3＝AB＝2，所以Q3点的坐标为（1，﹣2），
②当AB为菱形的对角线时，如图所示的菱形AP4BQ4，
设菱形的边长为x，则在Rt△AP4O中，AP42＝AO2+P4O2，即x2＝12+（﹣x）2，解得x＝，
所以Q4（1，）．
综上可得，平面内满足条件的Q点的坐标为：Q1（﹣1，0），Q2（1，2），Q3（1，﹣2），Q4（1，）．

19．【解答】解：（1）∵直线y＝﹣x+4与坐标轴分别交于点A、B，
∴x＝0时，y＝4，y＝0时，x＝8，
∴＝＝，
当t秒时，QO＝FQ＝t，则EP＝t，
∵EP∥BO，
∴＝＝，
∴AP＝2t，
∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动，
∴点P运动的速度是每秒2个单位长度；

（2）如图1，当PQ＝PE时，矩形PEFQ为正方形，
则∵OQ＝FQ＝t，PA＝2t，
∴QP＝8﹣t﹣2t＝8﹣3t，
∴8﹣3t＝t，
解得：t＝2；
如图2，当PQ＝PE时，矩形PEFQ为正方形，
∵OQ＝t，PA＝2t，
∴OP＝8﹣2t，
∴QP＝t﹣（8﹣2t）＝3t﹣8，
∴t＝3t﹣8，
解得：t＝4；

（3）如图1，当Q在P点的左边时，
∵OQ＝t，PA＝2t，
∴QP＝8﹣t﹣2t＝8﹣3t，
∴S矩形PEFQ＝QP•QF＝（8﹣3t）•t＝8t﹣3t2，
当t＝﹣＝时，
S矩形PEFQ的最大值为：＝，
如图2，当Q在P点的右边时，
∵OQ＝t，PA＝2t，
∴2t＞8﹣t，
∴t，
∴QP＝t﹣（8﹣2t）＝3t﹣8，
∴S矩形PEFQ＝QP•QF＝（3t﹣8）•t＝3t2﹣8t，
∵当点P、Q其中一点停止运动时，另一点也停止运动，
∴＜t≤4，
∴t＝4时，S矩形PEFQ的最大值为：3×42﹣8×4＝16，
综上所述，当t＝4时，S矩形PEFQ的最大值为：16．


20．【解答】解：（1）如图1，∵AB⊥x轴正半轴于点A，AD是∠BAO外角的角平分线，
∴∠DAB＝45°，
∵BD⊥AD，
∴∠DBA＝45°，
∴△ABD是等腰直角三角形，
作DE⊥AB于D，
∴DE＝AE＝AB，
∵B（2，8），
∴AE＝DE＝4，
∴D（6，4）；
（2）如图2，∵B（2，8），D（6，4），
∴直线BD的解析式为y＝﹣x+10，
∴直线BD与y轴的交点F的坐标为（0，10），
∵AB∥y轴，BD∥PQ，
∴四边形DQGF是平行四边形，
∴FG＝PB＝2t，
∴OG＝10﹣2t，PA＝8﹣2t，
∵BD∥PQ，
∴PQ⊥AD，
∴△APQ是等腰直角三角形，
∴PQ＝AQ＝AP＝（8﹣2t），
∴S＝S梯形APGO+S△PAQ＝（8﹣2t+10﹣2t）×2+×（8﹣2t）×（8﹣2t），
＝t2﹣12t+34，
即S＝t2﹣12t+34，（0≤t≤4）；
（3）如图3，∵Rt△OAP的两直角边的比为2：1，OA＝2，
∴AP＝4或1，
当AP＝4时，则P（2，4），
∵BD∥PQ，直线BD的解析式为y＝﹣x+10，
∴设直线PQ的解析式为y＝﹣x+n，
把P（2，4）代入得，4＝﹣2+n，交点n＝6，
∴直线PQ的解析式为y＝﹣x+6，
∴M（6，0）；
当AP＝1时，则P（2，1），
同理，即可求得M（3，0），
∴P的坐标为（6，0）或（3，0）．