第十七章 勾股定理 章节复习（导学案）-八年级数学下册同步备课系列（人教版）

人教版初中数学八年级下册

第十七章 勾股定理 章节复习 导学案

一、学习目标：

1.复习与回顾本章的重要知识点;

2.勾股定理及其逆定理的用途和相互关系;

3.总结本章的重要思想方法及其应用;

4.勾股定理及逆定理的综合运用.

二、学习过程：

知识梳理

一、勾股定理

勾股定理：_________________________________________________________

____________________________________________________________.

_________________       _________________    __________________

_________________       _________________    __________________

二、勾股定理的实际应用

利用勾股定理解决实际问题的一般步骤：

（1）_____________________________________________________；

（2）_____________________________________________________；

（3）_____________________________________________________；

（4）_____________________________________________________.

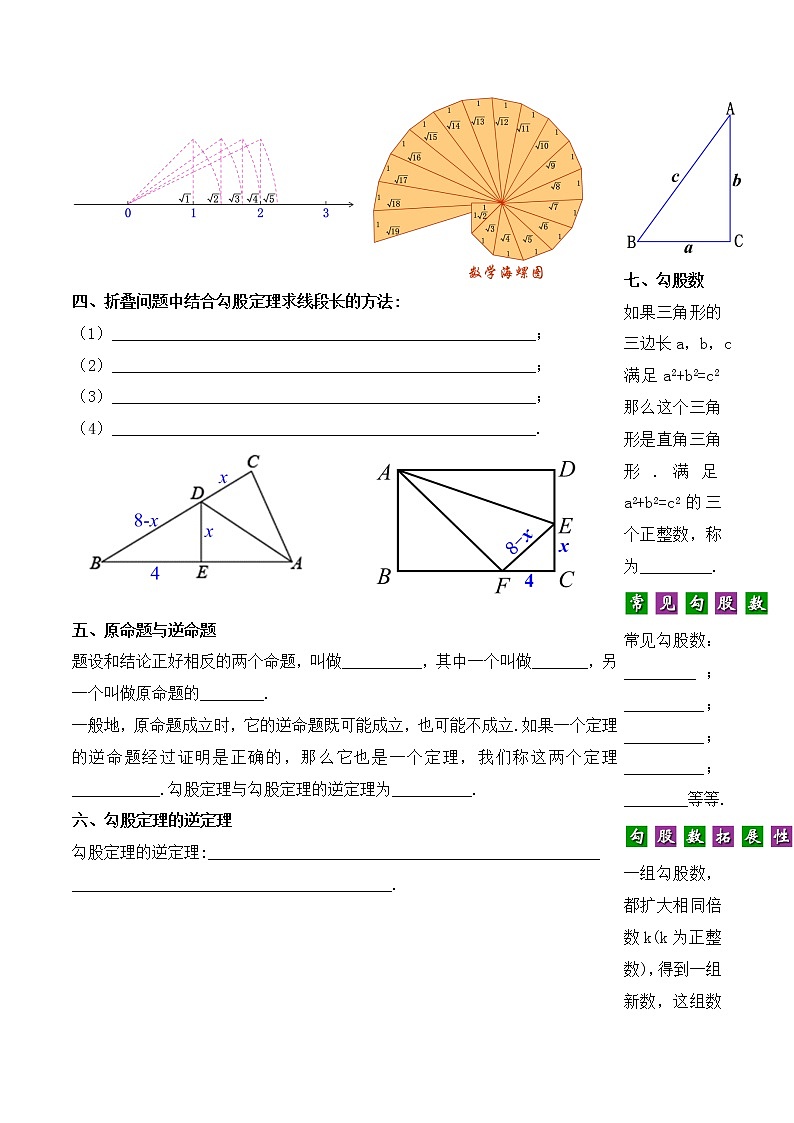
三、利用勾股定理表示无理数的方法:

（1）_______________________________________________________________

__________________________________________________________；

（2）______________________________________________________________

___________________________________________________________；

类似地，利用勾股定理，可以作出长为，，，…的线段. 按照同样方法，可以在数轴上画出表示，，，，，…的点.

四、折叠问题中结合勾股定理求线段长的方法:

（1）_____________________________________________________；

（2）_____________________________________________________；

（3）_____________________________________________________；

（4）_____________________________________________________.

五、原命题与逆命题

题设和结论正好相反的两个命题，叫做__________，其中一个叫做_______，另一个叫做原命题的________.

一般地，原命题成立时，它的逆命题既可能成立，也可能不成立.如果一个定理的逆命题经过证明是正确的，那么它也是一个定理，我们称这两个定理___________.勾股定理与勾股定理的逆定理为__________.

六、勾股定理的逆定理

勾股定理的逆定理:_________________________________________________

________________________________________.

七、勾股数

如果三角形的三边长a，b，c满足a2+b2=c2那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数，称为_________.

常见勾股数：_________；__________；__________；__________；________等等.

一组勾股数，都扩大相同倍数k(k为正整数)，得到一组新数，这组数同样是勾股数.如：__________；__________；__________；__________；…

考点解析

考点1：勾股定理的简单应用

例1.在Rt△ABC中， ∠C=90°.

（1）若a:b=1:2 ，c=5,求a;

（2）若b=15，∠A=30°,求a,c.

例2.已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.

例3.以直角三角形的三边为边向外作正方形，如图①所示，三个正方形的面积分别为S1，S2，S3，则有S1+S2___S3(填“>”“=”“<”).

(1)分别以直角三角形的三边为直径向外作半圆，如图②所示，上述结论是否仍成立?说明理由.

(2)分别以直角三角形的三边为斜边向外作等腰直角三角形，(1)中的结论仍成立吗(直接写出结论，无需证明)?

(3)(变式拓展)如图③,图中数字代表正方形的面积,∠ACB=120°，求正方形P的面积.

【迁移应用】

【1-1】如图是我国古代著名的“赵爽弦图”的示意图，观察图形,可以验证的式子为(   )

A.(a+b)(a-b)=a2-b2   B.(a+b)2=a2+2ab+b2     C.c2=a2+b2          D.(a-b)2=a2-2ab+b2

【1-2】在直角三角形中，若两直角边长分别为3和4，则斜边长是(   )

A.5       B.7       C.       D.或5

【1-3】设直角三角的两条直角边长分别为a和b,斜边长为c.

(1)已知a=5，c=10， 求b;

(2)已知a=8，b=15， 求c;

(3)已知c=2.5，b=1.5，求a.

【1-4】如图，图中所有的三角形都是直角三角形，四边形都是正方形，已知正方形A，B，C，D的边长分别是12，16，9，12，求最大正方形E的面积.

考点2：勾股定理的实际应用

例4.如图，有两棵树，一棵树高AC是10米，另一棵树高BD是4米，两树相距8米（即CD=8米），一只小鸟从一棵树的树梢A点处飞到另一棵树的树梢B点处，则小鸟至少要飞行多少米？

例5.如图，甲乙两船同时从A港出发，甲船沿北偏东35°的方向，航速是12海里/时，2小时后，两船同时到达了目的地．若C、B两岛的距离为30海里，问乙船的航速是多少？

例6.有一个圆柱形油罐，要以A点环绕油罐建梯子，正好建在A点的正上方点B处,问梯子最短需多少米(已知油罐的底面半径是2m,高AB是5m,π取3）?

【迁移应用】

【2-1】如图，在离水面高度为米的岸上，有人用绳子拉船靠岸，开始时绳子的长为米，此人以米每秒的速度收绳，秒后船移动到点的位置，问船向岸边移动了多少米？（假设绳子是直的，结果保留根号）

【2-2】如图，有一个圆柱体，它的高为12厘米，底面半径为3厘米，在圆柱下底面的A点有一只蚂蚁，它想吃到上底面与A点相对的B处的食物，需要爬行的最短路程是多少?(π的值取3)

【2-3】如图，铁路和公路在点O处交汇．公路上距离O点的A处与铁路的距离是．如果火车行驶时，周围以内会受到噪音的影响，那么火车在铁路上沿方向以的速度行驶时，A处受噪音影响的时间是多少？

考点3：勾股定理的典型应用

例6.如图，数轴上点A所表示的数为a，求a的值.

例7.如图，在平面直角坐标系中有两点A(-3,5)，B(1,2)求A,B两点间的距离.

例8.如图，在2×2的方格中，小正方形的边长是1，点A、B、C都在格点上，求AB边上的高.

例9.如图，折叠长方形ABCD的一边AD，使点D落在BC边的F点处，若AB=8cm，BC=10cm，求EC的长.

【迁移应用】

【3-1】如图，点A表示的实数是（　 ）

A.               B.            C.-          D.-

【3-2】如图，在矩形ABCD中，AB=3，AD=1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴于点M，则点M表示的数为（　 ）

A.2             B.            C.            D.

【3-3】如图，将长方形纸片沿直线折叠，使点C落在边的中点处，点B落在点处，其中，求的长．

【3-4】如图，在平面直角坐标系中，每个小正方形的边长都是1．

(1)画出关于对称的；

(2)的面积为       ；

(3)在上画出点P，使的周长最小，最小周长是________．

考点4：勾股定理的逆定理及其应用

例10.若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c. 试判断△ABC的形状.

例11.已知的三条边长分别为，且，，（，是正整数）．是直角三角形吗？请证明你的判断．

例12.如图，在正方形ABCD中，F是CD的中点，E为BC上一点，且CE＝CB，试判断AF与EF的位置关系，并说明理由．

【迁移应用】

【4-1】下列各组数中，是勾股数的(   )

A.0.3，0.4，0.5    B.9，16，25       C.5，12，13      D.10，15，18

【4-2】下面三角形中是直角三角形的有(   )

①三角形三内角之比为1:2:3;

②三角形三内角之比为3:4:5;

③三角形三边之比为1:2:3;

④三角形三边之比为3:4:5.

A.1个       B.2个        C.3个         D.4个

【4-3】说出下列命题的逆命题.这些逆命题成立吗？

(1)两条直线平行，内错角相等；

(2)如果两个实数相等，那么它们的绝对值相等；

(3)全等三角形的对应角相等.

【4-4】根据下列条件，分别判断以为边的三角形是不是直角三角形．

(1)，，．

(2)，，．

(3)，，．

(4)，，（n为正整数）

(5)．

【4-5】已知中，、、所对边长分别为、、， 若、、三边满足，试判断的形状．

考点5：勾股定理及其逆定理综合应用

例13.如图，一块四边形花圃中，已知，，，，.

(1)求四边形花圃的面积；

(2)求到的距离．

例14.在一条东西走向的河流一侧有一村庄C，河边原有两个取水点A，B，其中，由于某种原因，由C到A的路现在已经不通，该村为方便村民取水，决定在河边新建一个取水点D（A、D、B在同一条直线上），并新修一条路，测得千米，千米，千米．求原来的路线的长．

例15.如图，某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行,“远航”号每小时航行16海里，“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q，R处，且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗？

例16.如图所示，在中，，且的周长为，点P从点A开始沿边向B点以每秒的速度移动；点Q从点B沿边向点C以每秒的速度移动，如果P、Q两点同时出发，经过3秒时，P、Q两点间的距离为多少？

【迁移应用】

【5-1】如图,有一块地，已知∠ADC=90°，AD=4m， CD=3m，AB=13m，BC=12m.求这块地的面积.

【5-2】如图，南北方向PQ以东为我国领海，以西为公海，晚上10时28分，我边防反偷渡巡逻101号艇在A处发现其正西方向的C处有一艘可疑船只正向我沿海靠近，便立即通知在PQ上B处巡逻的103号艇注意其动向，经检测，AC=10海里，BC=8海里，AB=6海里，若该船只的速度为12.8海里/时，则可疑船只最早何时进入我领海？

【5-3】某气象局监测到一个沙尘暴中心沿东西方向有A向B移动，已知点C处为以城镇，且点C与A、B两点的距离，以沙尘暴中心为圆心，周围以内都会受到沙尘暴影响．

(1)通过计算说明城镇C是否会受到影响；

(2)若沙尘暴中心的移动速度为，则沙尘暴影响该城镇持续的时间有多长？