第十七章 勾股定理（达标检测）-八年级数学下册同步备课系列（人教版）

第十七章 勾股定理 达标检测

一、单选题:

1．下面四组数，其中是勾股数组的是（    ）

A．，， B．，， C．，， D．，，

【答案】A

【分析】根据勾股数的定义：有a、b、c三个正整数，满足的三个数，称为勾股数．由此判定即可．

【详解】解：A、，能构成勾股数，故正确；

B、0.3，0.4，0.5，不是正整数，所以不是勾股数，故错误；

C、，不能构成勾股数，故错误；

D、，不能构成勾股数，故错误．

故选：A．

【点睛】本题考查了勾股数，解答此题要深刻理解勾股数的定义，熟记常用的勾股数．

2．在△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，下列结论中不正确的是（    ）

A．如果a2=b2−c2，那么△ABC是直角三角形且∠A=90°

B．如果∠A:∠B:∠C=1:2:3，那么△ABC是直角三角形

C．如果，那么△ABC是直角三角形

D．如果，那么△ABC是直角三角形

【答案】A

【分析】根据直角三角形的判定和勾股定理的逆定理解答即可．

【详解】解：A、如果 a2=b2-c2，即b2=a2+c2，那么△ABC 是直角三角形且∠B=90°，选项错误，符合题意；

B、如果∠A：∠B：∠C=1：2：3，由∠A+∠B+∠C=180°，可得∠A=90°，那么△ABC 是直角三角形，选项正确，不符合题意；

C、如果 a2：b2：c2=9：16：25，满足a2+b2=c2，那么△ABC 是直角三角形，选项正确，不符合题意；

D、如果∠A-∠B=∠C，由∠A+∠B+∠C=180°，可得∠A=90°，那么△ABC 是直角三角形，选项正确，不符合题意；

故选：A．

【点睛】本题考查的是直角三角形的判定和勾股定理的逆定理的应用，如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．

3．如图，字母B所代表的正方形的边长是（    ）

A．12 B．15 C．144 D．306

【答案】A

【分析】根据勾股定理求出字母B所代表的正方形的面积，根据正方形的性质计算，得到答案．

【详解】解：在Rt△DEF中，由勾股定理得，DF2＋EF2＝DE2，

∴字母B所代表的正方形的面积＝EF2＝DE2−DF2＝225−81＝144（cm2），

∴字母B所代表的正方形的边长＝12（cm），

故选A．

【点睛】本题考查的是勾股定理的应用、正方形的面积，熟知如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2＋b2＝c2是解决问题的关键．

4．已知一个直角三角形的两边长分别为和，则第三边长是（    ）

A． B． C． D．或

【答案】D

【分析】分为两种情况：斜边是有一条直角边是，和都是直角边，根据勾股定理求出即可．

【详解】解：如图，

分为两种情况：斜边是有一条直角边是，

由勾股定理得：第三边长是；

和都是直角边，

由勾股定理得：第三边长是；

即第三边长是或，

故选：D．

【点睛】本题考查了对勾股定理的应用，注意：在直角三角形中的两条直角边、的平方和等于斜边的平方．

5．如图，在的正方形网格中，每个小正方形的边长均为1，点，，都在格点上，若是的边上的高，则的长为（    ）

A． B． C． D．

【答案】D

【分析】根据勾股定理计算AC的长，利用割补法可得△ABC的面积，由三角形的面积公式即可得到结论．

【详解】解：由勾股定理得：AC＝，

∵S△ABC＝3×3−×1×2−×1×3−×2×3＝，

∴AC•BD＝，

∴•BD＝7，

∴BD＝．

故选：D．

【点睛】本题考查了勾股定理与三角形的面积的计算，掌握勾股定理是解题的关键．

6．如图，在矩形COED中，点D的坐标是，则CE的长是（    ）

A．3 B． C． D．4

【答案】C

【分析】根据勾股定理求得，然后根据矩形的性质得出．

【详解】解：∵四边形COED是矩形，

∴CE=OD，

∵点D的坐标是（1，3），

∴，

∴，

故选C．

【点睛】本题考查了矩形的性质以及勾股定理的应用，熟练掌握矩形的性质是解题的关键．

7．如图，一圆柱体的底面周长为10cm，高AB为12cm，BC是直径，一只蚂蚁从点A出发沿着圆柱的表面爬行到点C的最短路程为（　　）

A．17cm B．13cm C．12cm D．14cm

【答案】B

【分析】将圆柱的侧面展开，得到一个长方形，再然后利用两点之间线段最短解答．

【详解】解：如图所示：

由于圆柱体的底面周长为10cm，

则AD=10×=5（cm）．

又因为CD=AB=12cm，

所以AC=＝13（cm）．

故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是13cm．

故选：B．

【点睛】此题主要考查了平面展开图的最短路径问题，将圆柱的侧面展开，构造出直角三角形是解题的关键．

8．如图，已知中，，F是高和的交点，，，则线段的长度为（    ）

A． B．2 C． D．1

【答案】D

【分析】先证明△BDF≌△ADC，得到BF=AC=，再根据勾股定理即可求解．

【详解】解：∵和是△ABC的高线，

∴∠ADB=∠ADC=∠BEC=90°，

∴∠DBF+∠C=90°，∠CAD+∠C=90°，

∴∠DBF=∠CAD，

∵，

∴∠BAD=45°，

∴BD=AD，

∴△BDF≌△ADC，

∴BF=AC=，

在Rt△BDF中，DF=．

故选：D

【点睛】本题考查了全等三角形的判定与性质，勾股定理等知识，证明△BDF≌△ADC是解题关键．

9．如图，在矩形中，，，将矩形沿折叠，点落在点处，则重叠部分的面积为（    ）

A． B． C． D．

【答案】B

【分析】已知为边上的高，要求的面积，求得即可，求证，得，设，则在中，根据勾股定理求，于是得到，即可得到答案．

【详解】解：由翻折变换的性质可知：，

∴，，，

∵四边形为矩形，，，

∴，，，

∴，，

在和中，

，

∴，

∴，，

设，则，

在中，，

∴，

解得：，

∴，

∴．

故选：B．

【点睛】本题考查翻折变换―折叠问题，矩形的性质，全等三角形的判定和性质，勾股定理等知识点，应用了方程的思想．本题通过设，在中运用勾股定理建立关于的方程并求解是解题的关键．

10．如图，在中，，，点D，E为BC上两点．，F为外一点，且，，则下列结论：

①；②；③；④，其中正确的是   

A．①②③④ B．①②④ C．①③④ D．②③

【答案】A

【分析】①利用全等三角形的判定得≌，再利用全等三角形的性质得结论；②利用全等三角形的判定和全等三角形的性质得，再利用勾股定理得结论；③利用等腰三角形的性质得，再利用三角形的面积计算 结论；④利用勾股定理和等腰直角三角形的性质计算得结论．

【详解】解：如图：

对于①，因为，

所以，

，

因此．

又因为，

所以．

又因为，所以．

因此≌，所以．

故①正确．

对于②，由①知≌，所以．

又因为，

所以，连接FD，

因此≌．

所以．

在中，因为，

所以．

故②正确．

对于③，设EF与AD交于G．

因为，

所以．

因此．

故③正确．

对于④，因为，      

又在中，

又是以EF为斜边的等腰直角三角形，

所以

因此，

故④正确．

故选A．

【点睛】本题考查了全等三角形的判定，全等三角形的性质，勾股定理，等腰三角形的性质和三角形的面积．

二、填空题:

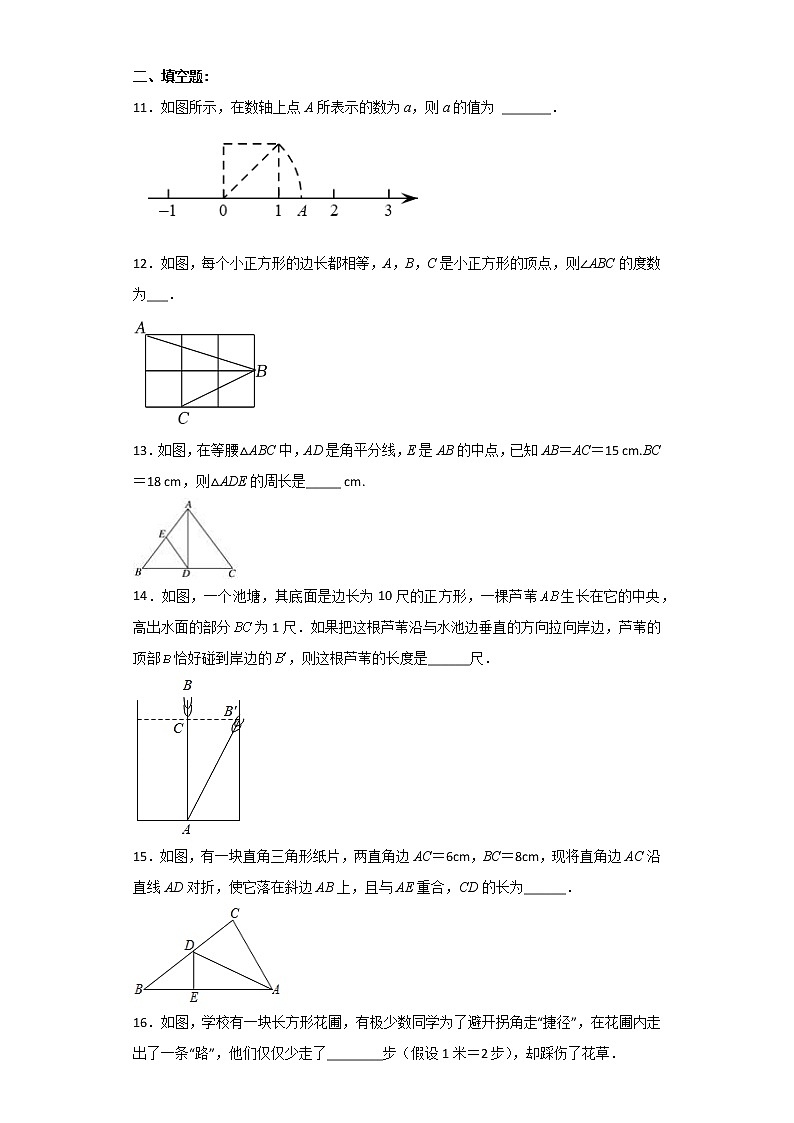
11．如图所示，在数轴上点A所表示的数为a，则a的值为 _______．

【答案】

【分析】先根据勾股定理求出直角三角形的斜边，即可求解．

【详解】解：如图：

由图可知：，

∵数轴上点A所表示的数为a，

∴，

故答案为：．

【点睛】本题考查了数轴和实数，勾股定理的应用，能读懂图是解此题的关键．

12．如图，每个小正方形的边长都相等，A，B，C是小正方形的顶点，则∠ABC的度数为___．

【答案】45°

【分析】根据勾股定理得到AB，BC，AC的长度，再判断△ABC是等腰直角三角形，进而得出结论．

【详解】解：如图，连接AC．

由题意，AC＝ ，BC＝，AB＝，

∴AC＝BC，AB2＝AC2+BC2，

∴△ABC是等腰直角三角形，且∠ACB＝90°，

∴∠ABC＝∠CAB＝45°．

故答案为：45°．

【点睛】本题考查了勾股定理及其逆定理，等腰直角三角形的判定与性质，判断出△ABC是等腰直角三角形是解决本题的关键．

13．如图，在等腰△ABC中，AD是角平分线，E是AB的中点，已知AB＝AC＝15 cm.BC＝18 cm，则△ADE的周长是_____ cm.

【答案】27

【分析】先根据勾股定理求出AD的长，再根据中点的性质求解即可.

【详解】解：在等腰△ABC中，AD是角平分线，E是AB的中点，

AB    BD=BC   AD

已知AB＝AC＝15 cm.   BC＝18 cm，

BD=9    DE=AC=7.5   AE=AB=7.5

AD=

△ADE的周长=AE+AD+DE=7.5+12+7.5=27

【点睛】此题重点考察学生对勾股定理的应用，熟练掌握勾股定理是解题的关键.

14．如图，一个池塘，其底面是边长为10尺的正方形，一棵芦苇生长在它的中央，高出水面的部分为1尺．如果把这根芦苇沿与水池边垂直的方向拉向岸边，芦苇的顶部恰好碰到岸边的，则这根芦苇的长度是______尺．

【答案】13

【分析】设出AB=AB'=x尺，表示出水深AC，根据勾股定理建立方程，求出的方程的解即可得到芦苇的长．

【详解】解：设芦苇长AB=AB′=x尺，则水深AC=(x-1)尺，

因为底面是边长为10尺的正方形，所以B'C=5尺

在Rt△AB'C中，52+(x-1)2=x2，

解之得x=13，

即芦苇长13尺．

故答案为：13．

【点睛】此题主要考查了勾股定理的应用，熟悉数形结合的解题思想是解题关键．

15．如图，有一块直角三角形纸片，两直角边AC＝6cm，BC＝8cm，现将直角边AC沿直线AD对折，使它落在斜边AB上，且与AE重合，CD的长为______．

【答案】3cm

【分析】由勾股定理求得AB=10cm，然后由翻折的性质求得BE=4cm，设DC=xcm，则BD=（8-x）cm，DE=xcm，在△BDE中，利用勾股定理列方程求解即可．

【详解】解：∵在Rt△ABC中，两直角边AC=6cm，BC=8cm，

由折叠的性质可知：DC=DE，AC=AE=6cm，∠DEA=∠C=90°，

∴BE=AB-AE=10-6=4（cm ），∠DEB=90°，

设DC=xcm，则BD=（8-x）cm，DE=xcm，

在Rt△BED中，由勾股定理得：BE2+DE2=BD2，

即42+x2=（8-x）2，

解得：x=3．

故答案为3cm．

【点睛】本题主要考查的是翻折变换以及勾股定理的应用，一元一次方程的解法，熟练掌握翻折的性质和勾股定理是解题的关键．

16．如图，学校有一块长方形花圃，有极少数同学为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了________步（假设1米＝2步），却踩伤了花草．

【答案】4

【分析】根据勾股定理求出“路”的长度，再根据少走的“路”计算出少走的长度，得出所需步数即可．

【详解】解：由勾股定理可得：“路”的长度，

∴，

∵1米＝2步，

∴少走了4步

故答案为：4．

【点睛】本题主要考查了勾股定理的运用，熟练掌握相关概念是解题关键．

17．如图，四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”，如果大正方形面积为169，且直角三角形中较短的直角边的长为5，则中间小正方形面积(阴影部分)为________．

【答案】49

【分析】设直角三角形中较长的直角边的长为a，利用勾股定理求得直角边的较长边，进一步求得阴影部分的面积即可．

【详解】解：设直角三角形中较长的直角边的长为a，由题意得

a2+52=169

解得：a=12，

则中间小正方形面积(阴影部分)为(12−5)2=49.

故答案为49.

【点睛】本题考查了勾股定理的应用.

18．如图，在平面直角坐标系中，，两点的坐标分别为和，为等边三角形，则点的坐标为______．

【答案】

【分析】过点A作AD⊥BC于D，根据等腰三角形三线合一的性质可得BD=CD，再求出点D的横坐标，然后利用勾股定理列式求出AD的长度，再写出点A的坐标即可．

【详解】如图，过点A作AD⊥BC于D，

∵B、C两点的坐标分别为(-2，0)和(6，0)，

∴BC=6-（-2）=8，

∵△ABC为等边三角形

∴AB=AC=BC=8，BD=CD=4，

∴点D的横坐标为6-4=2，

在Rt△ABD中，AD=，

所以，点A的坐标为(2，)，

故答案为：(2，)．

【点睛】本题考查了点的坐标，主要利用了等腰三角形三线合一的性质，勾股定理，作辅助线构造出直角三角形是解题的关键．

19．如图，等腰直角中，，D为的中点，，若P为上一个动点，则的最小值为_________．

【答案】

【分析】根据中点的含义先求解 作点C关于AB对称点，则，连接，交AB于P，连接，此时的值最小，由对称性可知 于是得到再证明，然后根据勾股定理即可得到结论．

【详解】解：为的中点，

作点C关于AB对称点，交于，则，连接，交AB于P，连接．

此时的值最小．

由对称性可知   

∴

∴，点C关于AB对称点，

∴AB垂直平分，

∴

根据勾股定理可得

故答案为：．

【点睛】此题考查了轴对称-线路最短的问题，等腰直角三角形的性质与判定，勾股定理的应用，确定动点P何位置时，使PC+PD的值最小是解题的关键．

20．如图，在Rt△ABC中，∠ACB＝90°，AB＝12cm，∠BAC＝60°，动点M从点B出发，在BA边上以每秒2cm的速度向点A匀速运动，同时动点N从C出发，在CB边上以每秒cm的速度向B匀速运动，设运动时间为t秒(0＜t＜6)，连接MN，若△BMN是等腰三角形，则t的值为_____．

【答案】3s或（12﹣18）s或s．

【分析】分三种情形：①当MN＝MB时②当BM＝BN时③当MN＝BN时，分别求解即可；

【详解】解：分三种情形：①当MN＝MB时，作MH⊥BC于H，则HB＝HN．

在Rt△ABC中，∵∠A＝60°，∠C＝90°，AB＝12cm，

∴BC＝AB•sin60°＝6 ，∠B＝30°，

∵BM＝2t，CN＝t，

∴BN＝6﹣t＝2（BM•cos30°），

∴6﹣t＝t，

∴t＝3．

②当BM＝BN时，6﹣t＝2t，

∴t＝12﹣18．

③当MN＝BN时，同法可得：2t＝2•（6 ﹣t）•cos30°，解得t＝，

综上所述，若△BMN是等腰三角形，则t的值为3s或（12﹣18）s或s．

【点睛】本题考查勾股定理，解直角三角形，等腰三角形的判定和性质等知识，解题的关键是利用参数构建方程解决问题，属于中考常考题型．

三、解答题:

21．已知：如图，，，，，，求四边形的面积．

【答案】36

【分析】利用勾股定理求出BC，再利用勾股定理的逆定理证出△BCD是直角三角形，得到四边形的面积就等于两个直角三角形的面积之和.

【详解】∵∠A=90°，AB=4，AC=3，

∴．

∵BC=5，BD=12，CD=13，

∴，

∴△BCD是直角三角形，且斜边为CD，

∴．

即四边形ABCD的面积为36．

【点睛】此题考查的是勾股定理及勾股定理的逆定理，利用勾股定理逆定理判定△BCD是直角三角形是解决此题的关键.

22．如图，将矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上F点处，已知CE＝3cm，AB＝8cm，求图中阴影部分的面积．

【答案】30．

【分析】根据折叠的过程以及矩形的对边相等，得：AF＝AD＝BC，DE＝EF．然后根据勾股定理求得CF的长，再设BF＝x，即可表示AF的长，进一步根据勾股定理进行求解．

【详解】解：∵四边形ABCD是矩形，

∴AB=CD，AD=BC，

由折叠可知△ADE和△AFE关于AE成轴对称，

故AF＝AD，EF＝DE＝DC﹣CE＝8﹣3＝5cm．

在△CEF中，CF＝=4cm，

设BF＝xcm，则AF＝AD＝BC＝（x+4）cm．

在Rt△ABF中，由勾股定理，得82+x2＝（x+4）2．

解得x＝6，故BC＝10．

所以阴影部分的面积为：10×8﹣2S△ADE＝80﹣50＝30（cm2）．

【点睛】此题考查勾股定理的实际应用，矩形的性质，折叠的性质，正确分析图形得到直角三角形，利用勾股定理解决问题是解题的关键．

23．如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13米，此人以0.5米/秒的速度收绳，10秒后船移动到点D的位置，问船向岸边移动了多少米？(假设绳子是直的，结果保留根号)

【答案】船向岸边移动了(12－)米

【分析】在Rt△ABC中，利用勾股定理计算出AB长，再根据题意可得CD长，然后再次利用勾股定理计算出AD长，再利用BD=AB-AD可得BD长．

【详解】解：∵在Rt△ABC中，∠CAB＝90°，BC＝13米，AC＝5米，    

∴AB＝＝12(米)，

由题意，得CD＝13－0.5×10＝8(米)，

∴AD＝＝＝ (米)，

∴BD＝AB－AD＝(12－)米，

答：船向岸边移动了(12－)米．

【点睛】本题主要考查了勾股定理的应用，关键是掌握从题中抽象出勾股定理这一数学模型，领会数形结合的思想的应用．

24．如图，四边形ABCD，AB＝AD＝2，BC＝3，CD＝1，∠A＝90°，求∠ADC的度数．

【答案】135°.

【分析】首先在Rt△BAD中，利用勾股定理求出BD的长，求出∠ADB=45°，再根据勾股定理逆定理在△BCD中，证明△BCD是直角三角形，即可求出答案．

【详解】解　连接BD，

在Rt△BAD中，

∵AB＝AD＝2，

∴∠ADB＝45°，BD＝＝2，

在△BCD中，

DB2＋CD2＝(2)2＋12＝9＝CB2，

∴△BCD是直角三角形，

∴∠BDC＝90°，

∴∠ADC＝∠ADB＋∠BDC＝45°＋90°＝135°.

故答案为135°.

【点睛】此题主要考查了勾股定理以及逆定理的运用，解决问题的关键是求出∠ADB=45°，再求出∠BDC=90°．

25．如图，一个牧童在小河的南4华里（长度单位）的A处牧马，而他正位于他的小屋B的西8华里北7华里处，他想把他的马牵到小河边去饮水，然后回家，他要完成这件事情所走的最短路程是多少?

【答案】17华里

【分析】作出A点关于MN的对称点，连接交MN于点P，则就是最短路线，根据垂直平分线的性质，得出，根据勾股定理得出，即可求出最短路径．

【详解】解：作出A点关于MN的对称点，连接交MN于点P，则就是最短路线，如图所示：

，，，

∵MN垂直平分，

∴，

∵在中，，

∴，

∴（华里）．

答：牧童所走的最短里程是17华里．

【点睛】本题主要考查了垂直平分线的性质，勾股定理，根据题意作出最短路径，是解题的关键．

26．已知正方形ABCD的边长为4，E为AB的中点，F为AD上一点，且AF=AD，试判断△EFC的形状．

【答案】△EFC为直角三角形，理由见解析

【分析】因为正方形ABCD的边长为4，易得AF＝1，则FD＝3，DC＝BC＝4，AE＝EB＝2；在Rt△AEF、Rt△DFC，Rt△EBC中，利用勾股定理求出EF、EC、FC的长，再根据勾股定理的逆定理解答．

【详解】解：△EFC为直角三角形．

∵正方形ABCD的边长为4，AF=AD

∴AF=1，FD=3，DC=BC=4，

∵E为AB的中点，

∴AE=EB=2；

在Rt△AEF中，EF=；

在Rt△DFC中，FC==5；

在Rt△EBC中，EC==2．

∴EC2+EF2=FC2，

∴△EFC是直角三角形．

【点睛】本题考查了勾股定理和勾股定理的逆定理及正方形的性质，利用勾股定理求出三角形三边长，再利用勾股定理逆定理解答是解答此题的关键．

27．如图1，中，，，，点D为斜边上动点．

（1）如图2，过点D作交CB于点E，连接AE，当AE平分时，求CE；

（2）如图3，在点D的运动过程中，连接CD，若为等腰三角形，直接写出AD的值．

【答案】（1）7.5；（2）15或12.5或18

【分析】（1）由△ACE≌△ADE（AAS），推出CE=DE，AC=AD=15，设CE=x，则BE=20-x，BD=25-15=10，在Rt△BED中根据勾股定理即可解决问题；

（2）分两种情形分别求解即可解决问题；

【详解】解：（1）∵AC⊥CB，AC=15，AB=25

∴BC=20，

∵AE平分∠CAB，

∴∠EAC=∠EAD，

∵AC⊥CB，DE⊥AB，

∴∠EDA=∠ECA=90°，

∵AE=AE，

∴△ACE≌△ADE（AAS），

∴CE=DE，AC=AD=15，

设CE=x，则BE=20-x，BD=25-15=10

在Rt△BED中

∴x2+102=（20-x）2，

∴x=7.5，

∴CE=7.5．

（2）①当AD=AC时，△ACD为等腰三角形

∵AC=15，

∴AD=AC=15．

②当CD=AD时，△ACD为等腰三角形

∵CD=AD，

∴∠DCA=∠CAD，

∵∠CAB+∠B=90°，

∠DCA+∠BCD=90°，

∴∠B=∠BCD，

∴BD=CD，

∴CD=BD=DA=12.5，

③当CD=AC时，△ACD为等腰三角形，

如图1中，作CH⊥BA于点H，

则AB•CH=AC•BC，

∵AC=15，BC=20，AB=25，

∴CH=12，

在Rt△ACH中，AH==9，

∵CD=AC，CH⊥BA，

∴DH=HA=9，

∴AD=18．

综上所述：AD的值为15或12.5或18．

【点睛】本题考查解直角三角形的应用，等腰三角形的判定和性质，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．