



高中数学5.4 三角函数的图象与性质随堂练习题
展开
这是一份高中数学5.4 三角函数的图象与性质随堂练习题,文件包含541正弦函数余弦函数的图象解析版docx、541正弦函数余弦函数的图象原卷版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。
一、正弦函数、余弦函数图象的画法
1.描点法:按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法.
2.几何法:利用三角函数线作出正弦函数和余弦函数在内的图象,再通过平移得到和的图象.
3.五点法:先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点,再利用光滑曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象.
在确定正弦函数在上的图象时,关键的五点是:
【注意】
(1)若,可先作出正弦函数、余弦函数在上的图象,然后通过左、右平移可得到和的图象.
(2)由诱导公式,故的图象也可以将的图象上所有点向左平移个单位长度得到.
二、正(余)弦函数的图象
三、用三角函数图象解三角不等式的方法
1、作出相应正弦函数或余弦函数在[0,2π]上的图象;
2、写出适合不等式在区间[0,2π]上的解集;
3、根据公式一写出不等式的解集.
题型一 五点法作三角函数的图象
【例1】用“五点法”作y=2sin2x的图象,首先描出的五个点的横坐标是( )
A. B. C. D.
【答案】B
【解析】由“五点法”作图知:令2x=0,,π,,2π,
解得x=0,,,,π,即为五个关键点的横坐标,故选:B.
【变式1-1】用“五点法”作函数,的大致图像,所取的五点是______.
【答案】,,,,
【解析】由“五点法”作函数,,的图象时的五个点分别是
,,,,.
【变式1-2】用“五点法”画出下列函数的简图:
(1),; (2),; (3),.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】(1)按五个关键点列表
描点并将它们用光滑的曲线连接起来如下图
(2)按五个关键点列表
描点并将它们用光滑的曲线连接起来如下图
(3)按五个关键点列表
描点并将它们用光滑的曲线连接起来如下图
【变式1-3】用“五点法”作下列函数的简图.
(1); (2). (3)().
【答案】(1)图象答案见解析;(2)图象答案见解析;(3)图象答案见解析.
【解析】(1)列表如下:
描点连线如图:
(2)列表如下:
描点连线如图:
(3)函数在长为一个周期的区间上的图象,列表如下:
再向左右两边扩展,其图象如下:
题型二 含绝对值的三角函数
【例2】函数y=|csx|的一个单调增区间是( )
A. B.[0,π] C. D.
【答案】D
【解析】将y=的图像位于x轴下方的图像关于x轴对称翻折到x轴上方,
x轴上方(或x轴上)的图像不变,即得y=|csx|的图像
根据各选项判断只有D选项正确. 故选:D.
【变式2-1】作出函数,的大致图像.
【答案】图见解析
【解析】函数,
其图如下所示:
【变式2-2】作出函数的大致图像.
【答案】图象见解析
【解析】列表
作图:先作出的图像,又原函数是偶函数,图像关于y轴对称,
即可作出的图像.
【变式2-3】作函数的图象.
【答案】图象见解析.
【解析】
故的图象是的图象在x轴下方的部分翻折到x轴上方后得到的图象,
如图
题型三 三角函数识图问题
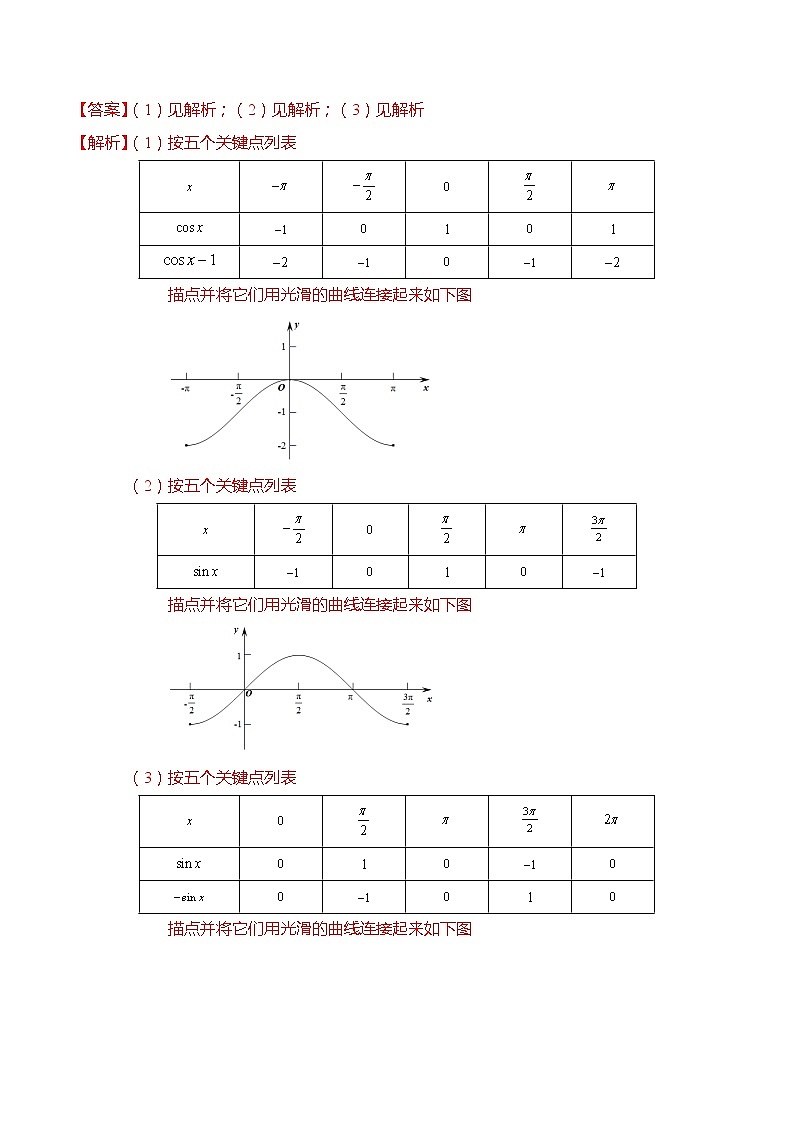
【例3】函数的大致图象是( )
A. B.
C. D.
【答案】A
【解析】函数是定义域上的奇函数
其图象关于原点对称,排除选项D;
当时,,此时,
∴当时,的图象在轴上方,排除选项B;
当时,,的图象在轴下方,排除选项C;
综上所述,函数的大致图象为选项A.故选:A.
【变式3-1】函数的图象大致是( )
A. B.
C. D.
【答案】A
【解析】令,则,排除C、D;
令,则,排除B.故选:A
【变式3-2】已知函数的图象如图所示,则此函数可能是( )
A. B.
C. D.
【答案】A
【解析】图象关于原点对称,为奇函数,CD中定义域是,不合,排除,
AB都是奇函数,当时,A中函数值为负,B中函数值为正,排除B.故选:A.
【变式3-3】已知函数的部分图象如图所示,则的解析式可能为( )
A. B. C. D.
【答案】B
【解析】对于A,,
所以函数为偶函数,故排除A;
对于D,,故排除D;
对于C,,则,
所以函数为奇函数,故排除C.故选:B.
题型四 利用图象解三角不等式
【例4】不等式的解集为( )
A. B. C. D.
【答案】B
【解析】
函数图象如下所示:
,
不等式的解集为:.故选:.
【变式4-1】在上,满足的的取值范围( )
A. B. C. D.
【答案】C
【解析】作出和在的函数图象,
根据函数图象可得满足的的取值范围为.故选:C.
【变式4-2】在内,不等式的解集是( )
A.(0,π) B. C. D.
【答案】C
【解析】画出y=sin x,的草图如下.
内,令,解得或,
结合图象可知不等式的解集为.故选:C.
【变式4-3】若函数的定义域为( )
A.() B.()
C.() D.()
【答案】B
【解析】要使函数有意义,则,即,
即,,得,,
即函数的定义域为().故选:B
【变式4-4】已知的定义域是,则的定义域为( )
A., B.,
C., D.,
【答案】A
【解析】的定义域是,故由可得,
解得,
因此,函数的定义域为.故选:A.
【变式4-5】函数y=的定义域是________.
【答案】
【解析】由知,,
由正弦函数图象特征知,.
故定义域为.
故答案为:.
题型五 与正余弦函数有关的零点
【例5】函数,的图像与直线的交点的个数为( )
A.0 B.1 C.2 D.3
【答案】C
【解析】在同一平面直角坐标系内,先画函数,的图像,再画直线,
可知所求交点的个数为2.故选:C.
【变式5-1】已知函数f(x)=-sinx,则f(x)在区间[0,2π]上的零点个数为( )
A.1 B.2 C.3 D.4
【答案】B
【解析】令,则,
在同一坐标系中,作出,如下图所示:
由图知,f(x)在区间[0,2π]上的零点个数为2个.故选:B.
【变式5-2】是定义在R上的偶函数,且,时,,则函数在区间上零点的个数为( )
A.2021 B.4043 C.2020 D.4044
【答案】B
【解析】,,即函数的周期为2,
当时,,则当时,,
由此可作出函数与函数的大致图象如下,
由图象可知,每个周期内有两个交点,
所以函数在区间上零点的个数为个.故选:B.
【变式5-3】函数的图象与直线有且仅有两个不同的交点,则k的取值范围是( )
A. B. C. D.
【答案】C
【解析】当时,,
当时,,
所以函数的图像如图所示,
所以函数的图象与直线有且仅有两个不同的交点时,.故选:C
【变式5-4】已知函数若在区间上至少有5个零点,在区间上至多有5个零点,则正数的取值范围是( )
A. B. C. D.
【答案】B
【解析】因为方程在上的解为,,
所以当在区间上至多有5个零点时,
因为方程在上的解为,,
所以当在区间上至少有5个零点时,,即
综上,正数的取值范围是,故选:B函数
y=sin x
y=cs x
图象
图象画法
五点法
五点法
关键五点
,,,,
,,,,
正(余)弦曲线
正(余)弦函数的图象叫做正(余)弦曲线
x
0
0
2
0
-2
0
x
0
1
0
-1
0
x
0
y
0
2
0
-2
0
x
0
0
1
0
-1
0
相关试卷
这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质练习,共31页。
这是一份人教A版 (2019)必修 第一册5.4 三角函数的图象与性质课时作业,共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质优秀课时训练,文件包含541正弦函数余弦函数的图象原卷版docx、541正弦函数余弦函数的图象解析版docx等2份试卷配套教学资源,其中试卷共22页, 欢迎下载使用。










