


初中北师大版4 用尺规作角获奖ppt课件
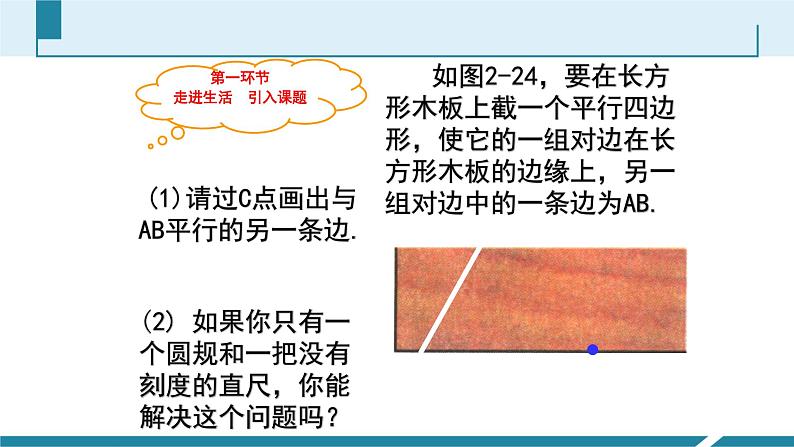
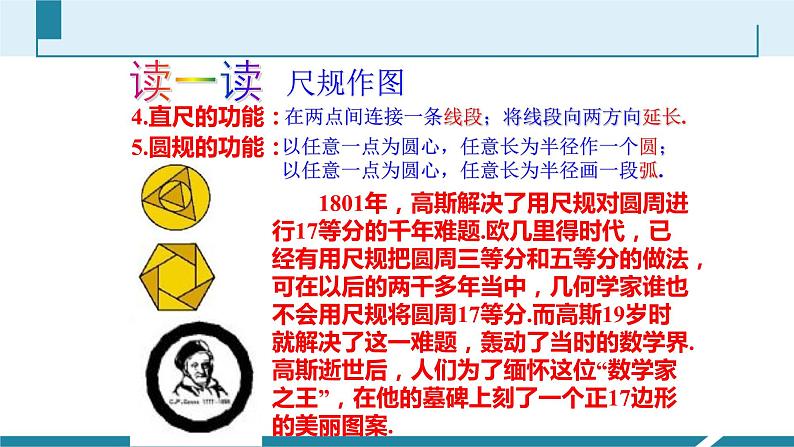
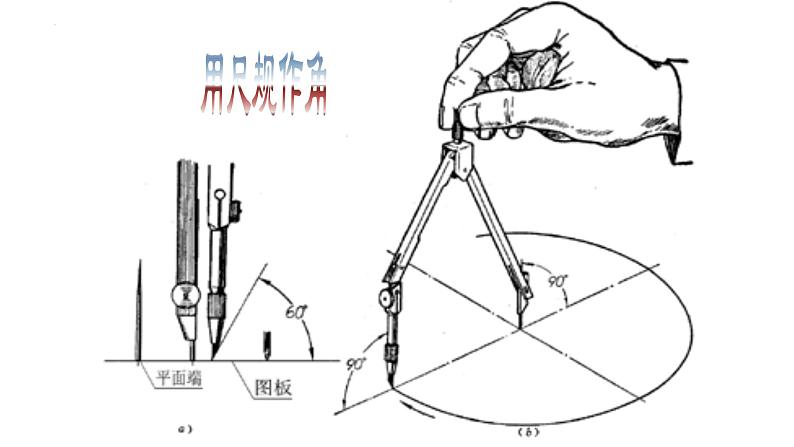
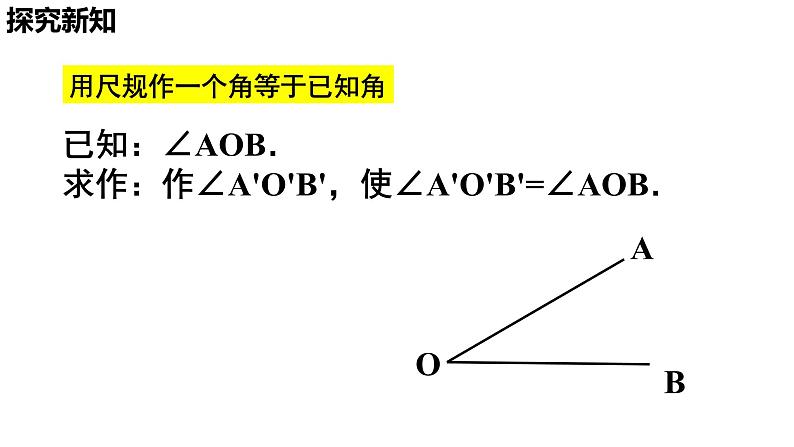
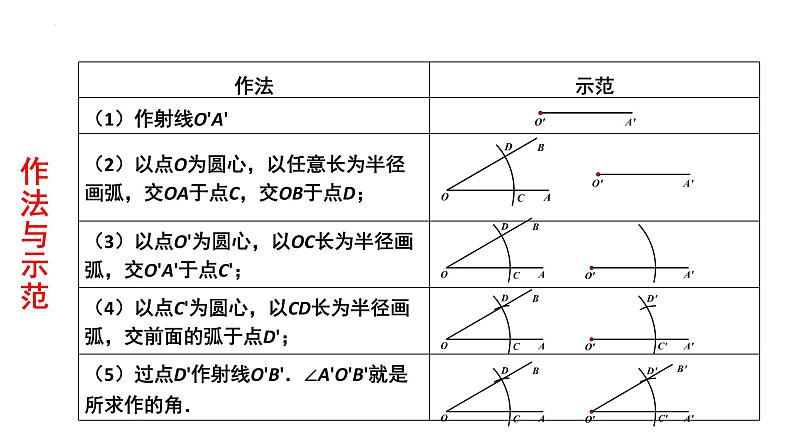
展开北师大版七年级下册2.4 尺规作图第二章 相交线与平行线1191. 能按照作图语言来完成作图动作,能用尺规作一个角等于已知角,并了解它在尺规作图中的简单应用.2. 能利用尺规作角的和、差、倍.素养目标3. 在尺规作图过程当中,积累数学活动经验,培养动手能力和逻辑分析能力. 如图2-24,要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.请过C点画出与AB平行的另一条边.(2) 如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗?3.以理论形式明确规定:是欧几里得.读一读尺规作图1.尺规作图:就是只准有限次地使用没有刻度 的直尺和圆规进行作图.2.最早提出几何作图:古希腊的哲学家安那萨哥 拉斯,他因政治上的纠葛被关进监狱,并被 处死刑.在监狱里,为打发令人苦恼的生活. 他用一根绳子画圆,用破木棍、竹片作直尺, 当然这些尺上就不可能有刻度.另外,他的时 间也不多了,因此他想到要有限次地使用尺 规解决问题.读一读尺规作图4.直尺的功能:5.圆规的功能: 1801年,高斯解决了用尺规对圆周进行17等分的千年难题.欧几里得时代,已经有用尺规把圆周三等分和五等分的做法,可在以后的两千多年当中,几何学家谁也不会用尺规将圆周17等分.而高斯19岁时就解决了这一难题,轰动了当时的数学界.高斯逝世后,人们为了缅怀这位“数学家之王”,在他的墓碑上刻了一个正17边形的美丽图案.在两点间连接一条线段;将线段向两方向延长.以任意一点为圆心,任意长为半径作一个圆;以任意一点为圆心,任意长为半径画一段弧.用尺规作角已知:∠AOB.求作:作∠A'O'B',使∠A'O'B'=∠AOB.用尺规作一个角等于已知角ABO探究新知作法与示范例1 要在长方形木板上截一个平行四边形,使它的一组对边在长方形木板的边缘上,另一组对边中的一条边为AB.1. 请过C点画出与AB平行的另一边.2. 如果你只有一个圆规和一把没有刻度的直尺,你能解决这个问题吗? ABC提炼关键词语:已知角是 求作的角和已知角的大小关系是 .学以致用独立思考、口述作法、保留作图痕迹.作法一:∠A’OB’即为所求作的角.∠A’O’B’即为所求作的角.典型例题例2 已知∠AOB,尺规作图作∠A′O′B′,使∠A′O′B′=2∠AOB.独立思考、口述作法、保留作图痕迹.作法一:∠A’OB’即为所求作的角.∠A’O’B’即为所求作的角.例2 已知∠AOB,尺规作图作∠A′O′B′,使∠A′O′B′=2∠AOB.请用没有刻度的直尺和圆规, 完成本节课开始提出的问题.以点C为顶点作∠FCE =∠BAC,则∠FCE的边CF所在的直线即为所求.小试牛刀思考:用尺规作一个角等于已知角是尺规作图中的基本作图,你能利用它作出其他图形吗?提示:可以作角的和、差、倍角及与角有关的图.探究新知1.尺规作图的基本步骤: (1)写出已知.(2)写出求作.(3)写出作法并作图. 作图时要保留_________.有时,根据题目要求,可省略作法.作图痕迹3.作一个角等于已知角可以归纳为“一线三弧”先画一条射线,再作三次弧.其中前两次弧半径相同,而第三次以原角的两边与弧的交点之间的距离为半径.2.基础知识:1.用尺规作一个角等于已知角. 2.用尺规作一个角等于已知角的和、差、倍. 3.借助于已学的用尺规作线段和角来设计图案.尺规作角基本工具:画弧必备条件:无刻度直尺圆规基本步骤:三弧两线半径圆心《几何原本》是古希腊数学家欧几里德的一部不朽之作,集整个古希腊数学的成果和精神于一书。它是世界上最著名、最完整而且流传最广的的数学教科书,并且第一次完成了人类对空间的认识。书中系统地总结了古代劳动人民和学者们在实践和思考中获得的几何知识,并把公认的事实列成定义和公理,以形式逻辑的方法,用这些定义和公理来研究各种几何图形的性质,从而建立了一套从公理、定义出发,论证命题得到定理得几何学论证方法,形成了一个严密的逻辑体系--几何学。请用没有刻度的直尺和圆规, 在课本的图2-24中, 过点C作AB的平行线. 分析:若以点C为顶点作一个角∠FCE与∠BAC 相等,则∠FCE的边CF所在的直线即为所求.随堂练习2第二次“先学后教”:作一个角等于已知角的和、差、倍 CDC’D’课本56页议一议 1、用尺规作图比较两个角的大小已知: ∠AOB。利用尺规作: ∠A’O’B’ 使∠A’O’B’=2∠AOB。作法一:∠A’O’B’即为所求.2、作已知角的n倍的角(随堂练习1)(3) 过点B’作射线O’B’.已知: ∠AOB。利用尺规作: ∠A’O’B’, 使∠A’O’B’=2∠AOB。∠A’O’B’即为所求.(4) 以点C’为圆心,CD 长为半径画弧交前面的弧于点E,以点E为圆心, CD 长为半径画弧交前面的弧于点B ’ (5) 过点D’作射线O’B’.用尺规作优美的图案 右面的“邹菊图案”漂亮吗?你想自己画出它来吗?那就让我们从最初的步骤开始吧!4、继续作下去,在适当的区域涂上颜色,你作出美丽的“邹菊图案” 吗?图案设计用尺规作下面的图形:【第一关】1.下列作图:①用量角器画∠1=60°;②用圆规直尺作线段AB等于已知线段a;③用三角板画直线AB的垂线;④用刻度尺画线段AB=5 cm.其中,属于尺规作图的有 ( )A.1个 B.2个C.3个 D.4个A 2.下列关于尺规功能的说法不正确的是 ( )A.直尺的功能:在两点间连接一条线段或将线段向两方向延长B.直尺的功能:可作平角和直角C.圆规的功能:以任意长为半径,以任意点为圆心作一个圆D.圆规的功能:以任意长为半径,以任意点为圆心作一段弧3.已知∠α=40°,利用尺规作图作∠AOB=3∠α,如果OC是∠AOB的平分线,那么∠AOC=________.B 60° 【第二关】4.如图,已知∠ACB,请你利用尺规作图,在AC边的上方作∠CAE=∠ACB,写出作图方法,保留作图痕迹. 解:作法如下:(1)以点C为圆心,任意长为半径画弧,交射线CA于点F,交射线CB于点G;(2)以点A为圆心,线段CF为半径画弧,交射线AC于点H,以点H为圆心,线段FG为半径画弧,交前弧于点E;(3)画射线AE,∠CAE即为所求,如图.1、已知:∠1,∠2, (如图(1)所示),求作:∠AOB,使得∠AOB=∠1- ∠2。利用尺规作角的和与差课后作业2.已知:∠α,∠β(如图(1)所示),求作:∠AOB,使得∠AOB=∠α+∠β.平平安安回家高高兴兴上学再见
初中数学北师大版七年级下册第二章 相交线与平行线4 用尺规作角获奖ppt课件: 这是一份初中数学北师大版七年级下册第二章 相交线与平行线4 用尺规作角获奖ppt课件,共26页。PPT课件主要包含了学习目标,情境导入,探究新知,用尺规作角,归纳总结,测量法,叠合法,尺规作图法,例2已知∠1,1作射线OM等内容,欢迎下载使用。
北师大版七年级下册4 用尺规作角精品课件ppt: 这是一份北师大版七年级下册4 用尺规作角精品课件ppt
初中数学北师大版七年级下册第二章 相交线与平行线4 用尺规作角评优课课件ppt: 这是一份初中数学北师大版七年级下册第二章 相交线与平行线4 用尺规作角评优课课件ppt,共17页。PPT课件主要包含了素养目标,探究新知,作法与示范,学以致用,两角和,两角差等内容,欢迎下载使用。













