北师大版数学八年级上册《实数和二次根式》全章复习与巩固（提高）知识讲解 (含答案)

《实数和二次根式》全章复习与巩固（提高）

【学习目标】

1.了解算术平方根、平方根、立方根的概念，会用根号表示数的平方根、立方根.

2.了解开方与乘方互为逆运算，会用平方运算求某些非负数的平方根，会用立方运算求某些数的立方根，会用计算器求平方根和立方根.

3.了解无理数和实数的概念，知道实数与数轴上的点一一对应，有序实数对与平面上的点一一对应；了解数的范围由有理数扩大为实数后，概念、运算等的一致性及其发展变化.

4.能用有理数估计一个无理数的大致范围.

5.理解并掌握二次根式、最简二次根式、同类二次根式的定义和性质.

6.熟练掌握二次根式的加、减、乘、除运算，会用它们进行有关实数的四则运算.

7.了解代数式的概念，进一步体会代数式在表示数量关系方面的作用.

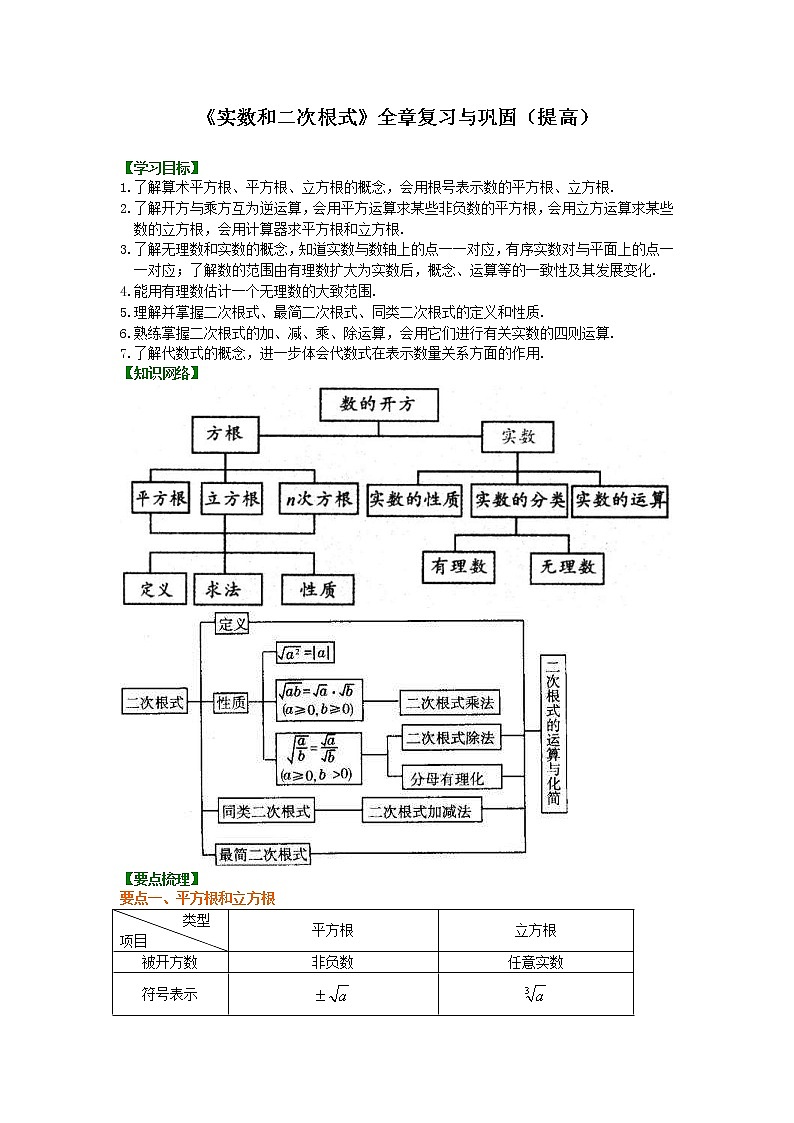
【知识网络】

【要点梳理】

要点一、平方根和立方根

要点二、无理数与实数

有理数和无理数统称为实数.
1.实数的分类

实数

要点诠释：（1）所有的实数分成三类：有限小数，无限循环小数，无限不循环小数．其中有限小数和无限循环小数统称有理数，无限不循环小数叫做无理数．

 （2）无理数分成三类：①开方开不尽的数，如，等；

②有特殊意义的数，如π；        

③有特定结构的数，如0.1010010001…

　 （3）凡能写成无限不循环小数的数都是无理数，并且无理数不能写成分数形式.

2.实数与数轴上的点一 一对应

数轴上的任何一个点都对应一个实数，反之任何一个实数都能在数轴上找到一个点与之对应.

3.实数的三个非负性及性质
　　在实数范围内，正数和零统称为非负数。我们已经学习过的非负数有如下三种形式：
　  （1）任何一个实数的绝对值是非负数，即||≥0；
　　（2）任何一个实数的平方是非负数，即≥0；
　　（3）任何非负数的算术平方根是非负数，即 ().
　　非负数具有以下性质：
　　（1）非负数有最小值零；
　　（2）有限个非负数之和仍是非负数；
　　（3）几个非负数之和等于0，则每个非负数都等于0.

4.实数的运算

数的相反数是－；一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；0的绝对值是0.

　　有理数的运算法则和运算律在实数范围内仍然成立.实数混合运算的运算顺序：先乘方、开方、再乘除，最后算加减.同级运算按从左到右顺序进行，有括号先算括号里.

5.实数的大小的比较
　　有理数大小的比较法则在实数范围内仍然成立.

　　法则1. 实数和数轴上的点一一对应，在数轴上表示的两个数，右边的数总比左边的数          大；

法则2．正数大于0，0大于负数，正数大于一切负数，两个负数比较，绝对值大的反而小；

　法则3. 两个数比较大小常见的方法有：求差法，求商法，倒数法，估算法，平方法.

要点三、二次根式的相关概念和性质

1. 二次根式

形如的式子叫做二次根式，如等式子，都叫做二次根式.

要点诠释：二次根式有意义的条件是，即只有被开方数时，式子才是二次根式，才有意义.

2.二次根式的性质

（1）；
（2）；
（3）.

要点诠释：（1） 一个非负数可以写成它的算术平方根的平方的形式，即 （），如（）.

（2） 中的取值范围可以是任意实数，即不论取何值，一定有意义.

（3）化简时，先将它化成，再根据绝对值的意义来进行化简.

（4）与的异同

不同点：中可以取任何实数，而中的必须取非负数；

=，=（）.

相同点：被开方数都是非负数，当取非负数时，=.

3. 最简二次根式

（1）被开方数是整数或整式；

（2)被开方数中不含能开方的因数或因式.

满足上述两个条件的二次根式，叫做最简二次根式.如等都是最简二次根式.

要点诠释：最简二次根式有两个要求：（1）被开方数不含分母；（2）被开方数中每个因式的指数都小于根指数2.

4.同类二次根式

几个二次根式化成最简二次根式后，被开方数相同，这几个二次根式就叫同类二次根式.

要点诠释：判断是否是同类二次根式，一定要化简到最简二次根式后，看被开方数是否相同，再判断.如与，由于=，与显然是同类二次根式.

要点四、二次根式的运算

1. 乘除法

（1）乘除法法则：

要点诠释：

（1）当二次根式的前面有系数时，可类比单项式与单项式相乘（或相除）的法则，如.

（2）被开方数一定是非负数（在分母上时只能为正数）.

如.

2.加减法

将二次根式化为最简二次根式后，将同类二次根式的系数相加减，被开方数和根指数不变，即合并同类二次根式.

要点诠释：二次根式相加减时，要先将各个二次根式化成最简二次根式，再找出同类二次根式，最后合并同类二次根式.如.

【典型例题】

类型一、有关方根的问题

1、已知，求的值.

【思路点拨】由被开方数是非负数，分母不为0得出的值，从而求出值，及的值.

【答案与解析】

解：由题意得

  ，解得＝－3

＝－2

∴＝.

【总结升华】根据使式子有意义的条件列出方程，解方程，从而得到的值.

2、（2020春•南昌期末）已知实数x、y满足，求2x﹣的立方根．

【答案与解析】

解：由非负数的性质可知：2x﹣16=0，x﹣2y+4=0，

解得：x=8，y=6．

∴2x﹣y=2×8﹣×6=8．

∴2x﹣的立方根是2．

【总结升华】本题主要考查的是非负数的性质、立方根的定义，求得x、y的值是解题的关键．

类型二、与实数有关的问题

3、已知是的整数部分，是它的小数部分，求的值．

【思路点拨】一个数是由整数部分＋小数部分构成的.通过估算的整数部分是3，那么它的小数部分就是，再代入式子求值.

【答案与解析】

解：∵是的整数部分，是它的小数部分，

∴

∴.

【总结升华】可用夹挤法来确定，即看介于哪两个相邻的完全平方数之间，然后开平方.这个数减去它的整数部分后就是它的小数部分.

举一反三：

【变式】 已知5＋的小数部分为，5－的小数部分为，则＋的值是      ；

－的值是_______.

【答案】；

提示：由题意可知，.

4、阅读理解，回答问题.

在解决数学问题的过程中，有时会遇到比较两数大小的问题，解决这类问题的关键是根据命题的题设和结论特征，采用相应办法，其中巧用“作差法”是解决此类问题的一种行之有效的方法：若－＞0，则＞；若－＝0，则＝；若－＜0，则＜.

例如：在比较与的大小时，小东同学的作法是：

    ∵

    ∴    

请你参考小东同学的作法，比较与的大小.

【思路点拨】仿照例题，做差后经过计算判断差与0的关系，从而比较大小.

【答案与解析】

解：∵

∴＜

【总结升华】实数比较大小常用的有作差法和作商法，根据具体情况加以选择.

举一反三：

【变式】实数在数轴上的位置如图所示，则的大小关系是：               ；

【答案】；

类型三、实数综合应用

5、阅读材料：

学习了无理数后，某数学兴趣小组开展了一次探究活动：估算的近似值.

小明的方法：

∵，设（）.∴.

∴.∴.解得 .∴.

问题：（1）请你依照小明的方法，估算的近似值；

（2）请结合上述具体实例，概括出估算的公式：已知非负整数、、，若，且，则_________________(用含、的代数式表示)；

（3）请用（2）中的结论估算的近似值.

【答案与解析】

解：（1）∵，设（）.

∴.

∴.∴.

解得 .

∴.

（2）∵，设（）.

∴.

∴.

∴.

对比，

∴

（3）

∴，

∴6.083.

【总结升华】此题比较新颖，关键是通过阅读材料快速掌握估值的方法.（2）问中要对比式子，找准和，表示出.

类型四、二次根式概念及运算

6、（2020春•石林县期末）计算：5+﹣×+÷．

【思路点拨】先二次根式化为最简二次根和根据二次根式的乘除法得到原式=+﹣+3÷=2﹣1+3，然后合并即可．

【答案与解析】

解：原式=+﹣+3÷

=2﹣1+3

=2+2．

【总结升华】本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后进行二次根式的加减运算．

举一反三：

【变式】. 

【答案】.

7、已知为△ABC的三边长，化简
　　　　　

【答案与解析】

解：∵为△ABC的三边长，

∴原式
　　　
【总结升华】利用三角形任意两边之和大于第三边和进行化简.
8、 若，化简.

【答案与解析】

【总结升华】把分子分母分别分解因式，然后约分，可以简化化简步骤.

举一反三：
【变式】当.

【答案】

解：

，

将代入，原式=3.