专题06 半角模型综合应用（专项训练）-备战中考数学《重难点解读•专项训练》（全国通用）

  专题06  半角模型综合应用（专项训练）

1．如图，在△ABC中，∠C＝90°，AC＝BC，M、N是斜边AB上的两点，且∠MCN＝45°，AM＝3，BN＝5，则MN＝　    　．

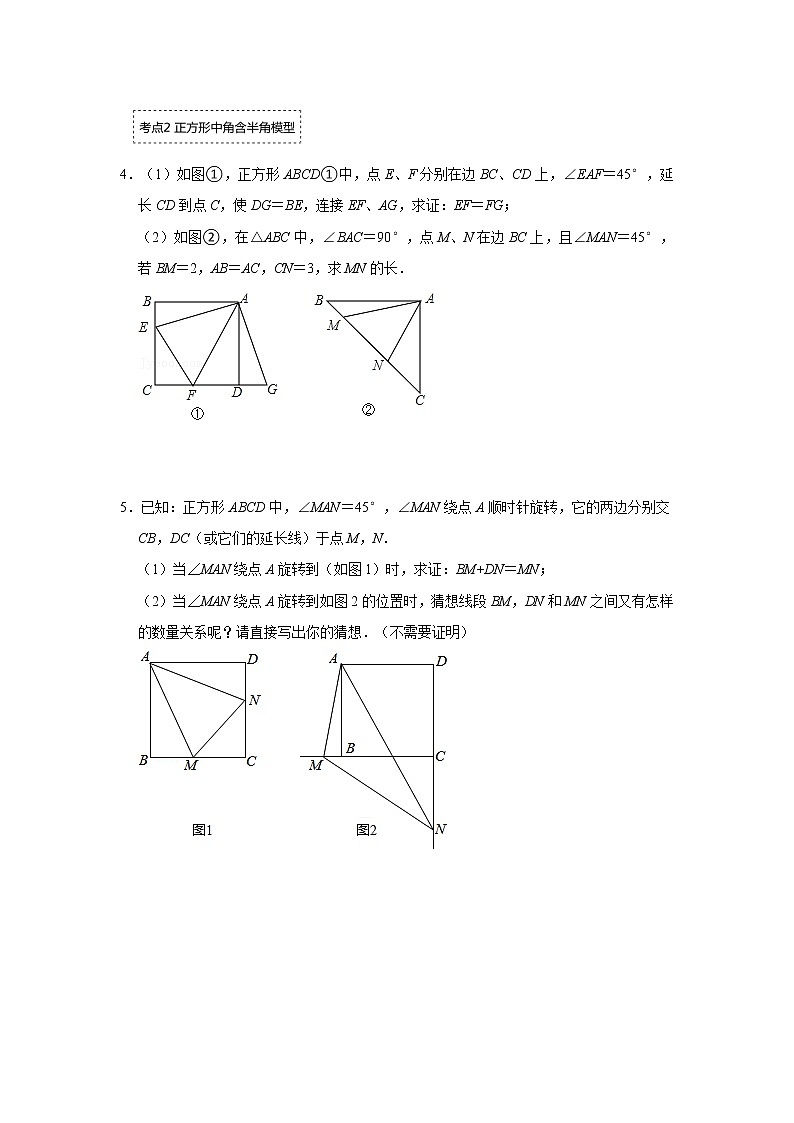
2．如图，在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC＝15，点M、N在边BC上，且∠MAN＝45°，CN＝5，MN＝　　．

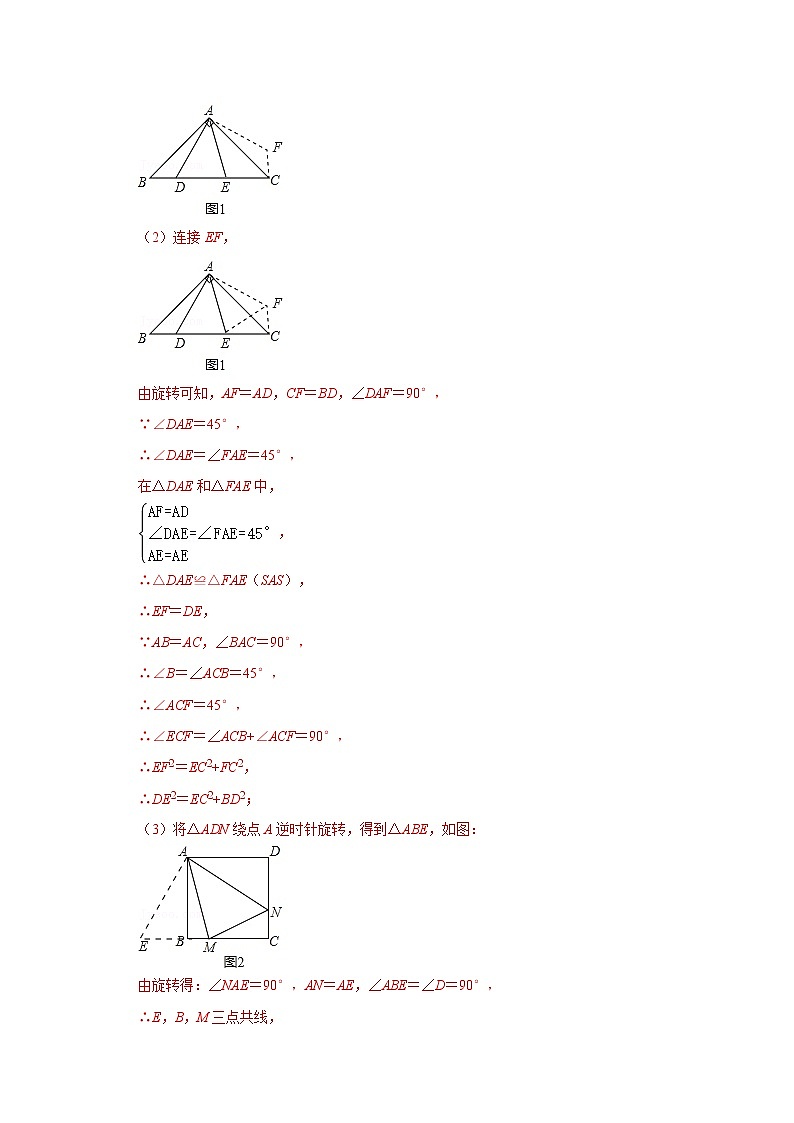
3．如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D、E是BC边上的任意两点，且∠DAE＝45°．

（1）将△ABD绕点A逆时针旋转90°，得到△ACF，请在图（1）中画出△ACF．

（2）在（1）中，连接EF，探究线段BD，EC和DE之间有怎样的数量关系？写出猜想，并说明理由．

（3）如图2，M、N分别是正方形ABCD的边BC、CD上一点，且BM+DN＝MN，试求∠MAN的大小．

4．（1）如图①，正方形ABCD①中，点E、F分别在边BC、CD上，∠EAF＝45°，延长CD到点C，使DG＝BE，连接EF、AG，求证：EF＝FG；

（2）如图②，在△ABC中，∠BAC＝90°，点M、N在边BC上，且∠MAN＝45°，若BM＝2，AB＝AC，CN＝3，求MN的长．

5．已知：正方形ABCD中，∠MAN＝45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N．

（1）当∠MAN绕点A旋转到（如图1）时，求证：BM+DN＝MN；

（2）当∠MAN绕点A旋转到如图2的位置时，猜想线段BM，DN和MN之间又有怎样的数量关系呢？请直接写出你的猜想．（不需要证明）

6．把一个含45°的三角板的锐角顶点与正方形ABCD的顶点A重合，然后把三角板绕点A顺时针旋转，它的两边分别交直线CB、DC于点M、N．

（1）当三角板绕点A旋转到图（1）的位置时，求证：MN＝BM+DN．

（2）当三角板绕点A旋转到图（2）的位置时，试判断线段MN、BM、DN之间具有怎样的等量关系？请写出你的猜想，并给予证明．

7．如图，在△ABC中，∠BAC＝120°，AB＝AC，点M、N在边BC上，且∠MAN＝60°．若BM＝2，CN＝3，则MN的长为　  　．

8．△ABC中，∠BAC＝α，AB＝AC，点D、E在直线BC上．

（1）如图1，D、E在BC边上，若α＝120°，且AD2+AC2＝DC2，求证：BD＝AD；

（2）如图2，D、E在BC边上，若α＝150°，∠DAE＝75°，且ED2+BD2＝CE2，求∠BAD的度数．

（3）如图3，D在CB的延长线上，E在BC边上，若∠BAC＝α，∠DAE＝180°﹣，∠ADB＝15°，BE＝4，BD＝2，则CD的值为 　   　．