（单元检测）第三单元长方体和正方体检测卷（C卷 拓展卷）-2022-2023学年五年级数学下册书山有路勤练系列（A3卷）人教版

这是一份（单元检测）第三单元长方体和正方体检测卷（C卷 拓展卷）-2022-2023学年五年级数学下册书山有路勤练系列（A3卷）人教版，共10页。

…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
绝密★启用前
2022-2023学年五年级数学下册
第三单元长方体和正方体检测卷（C卷˙拓展卷）

考试时间：80分钟；满分：102分

班级：姓名： 成绩:
注意事项：
1．答题前填写好自己的班级、姓名等信息。
2．请将答案正确填写在答题区域，注意书写工整，格式正确，卷面整洁。

卷面（2分）。我能做到书写工整，格式正确，卷面整洁。

一、知识空格填一填。（每空1分，共40分）
1．一个长方体的表面积为52平方厘米，底面积为12平方厘米，宽为3厘米，高为( )厘米。
2．有一个长方体，长、宽、高都是整厘米数，相邻三个面的面积分别是56cm2、24cm2和21cm2，这个长方体的体积是( )cm3。
3．一根6m长的方钢，把它横截成三段时表面积增加80dm2，原来方钢的体积是( )m3。
4．一个棱长是3米的正方体木块，如果把它锯成体积相等的8个小正方体，表面积增加( )平方米。
5．一个长方体的储藏室，三个面的面积分别是18m2、12m2、6m2，如果要在它的四周刷上油漆，至少要刷( ) m2，这个储藏室容积是( ) m3。储藏室里放着一些茶叶礼盒，每个礼盒的底面周长是108cm，高20cm，棱长总和是( )cm。
6．正方体的棱长是2cm，它的表面积是( )cm2，体积是( )cm3；用12个这样的正方体，拼成不同形状的长方体，当拼成长方体的表面积最小时，这个长方体的长、宽、高分别是( )cm、( )cm、( )cm，体积是( )cm3。
7．一根铁丝正好可以围成一个棱长是8cm的正方体，围成的正方体的体积是( )cm3；若将这根铁丝改围成一个长10cm，宽8cm的长方体，围成的长方体的表面积是( )cm2。
8．用10个棱长1厘米的小正方体拼在一起（如图），从正面、后面、左面、右面、上面看，所看到的图形的面积的和是( )平方厘米，将如图几何体补成一个正方体，至少要添上( )个相同的小正方体。

9．从下图的长方体里面锯出一个最大的正方体，正方体的体积是( )dm3，剩下部分的表面积最小是( )dm2。

10．一块长方体木料，截去一个高8cm的长方体后，表面积比原来减少，剩下的部分是一个正方体。原来这块长方体木料的体积是( )。

二、是非曲直辩一辩。（对的画√，错的画X，每题2分，共10分）
11．10立方米10立方厘米＝10.01立方米。( )
12．两个体积相等的长方体和正方体，长方体的表面积比正方体的表面积大。( )
13．从长方体的一个顶点处切去一个小正方体后，它的表面积不变，体积减少。( )
14．把一块不规则的橡皮泥捏成长方体形状（均为实心），橡皮泥的形状和体积都发生了改变。( )
15．如果一个长方体的长、宽、高都扩大到原来的2倍，那么表面积就扩大到原来的4倍，体积就扩大到原来的8倍。( )
三、众说纷纭选一选。（将正确的选项填在括号内，每题2分，共10分）
16．一个长方体包装盒，从里面量长30cm，宽20cm，里面的体积是15dm3。妈妈想用它包装一件长24cm、宽15cm、高30cm的玻璃器皿，是否能装得下？答：（    ）。
A．能 B．不能 C．纸箱大小无所谓 D．无法确定
17．下面的平面图形中，共有（    ）幅图是长、正方体表面的展开图。

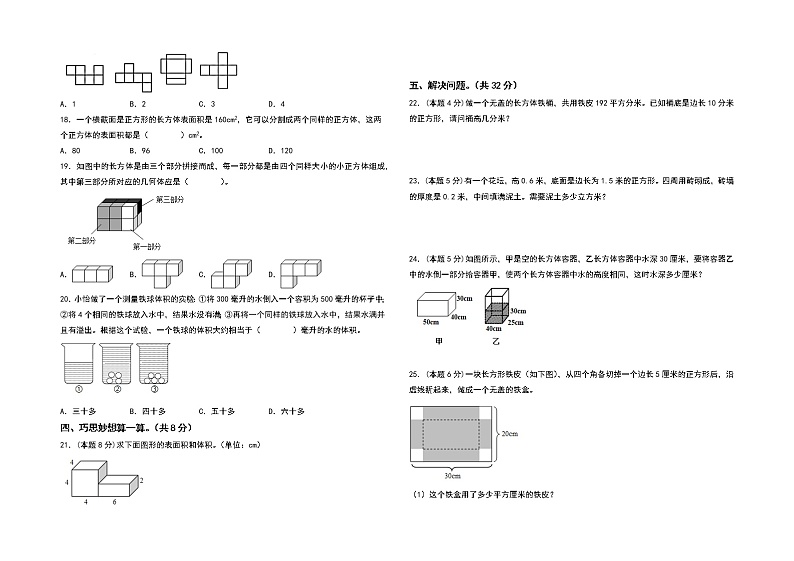
A．1 B．2 C．3 D．4
18．一个横截面是正方形的长方体表面积是160cm2，它可以分割成两个同样的正方体，这两个正方体的表面积都是（    ）cm2。
A．80 B．96 C．100 D．120
19．如图中的长方体是由三个部分拼接而成，每一部分都是由四个同样大小的小正方体组成，其中第三部分所对应的几何体应是（    ）。

A． B． C． D．
20．小怡做了一个测量铁球体积的实验：①将300毫升的水倒入一个容积为500毫升的杯子中；②将4个相同的铁球放入水中，结果水没有满；③再将一个同样的铁球放入水中，结果水满并且有溢出。根据这个试验，一个铁球的体积大约相当于（    ）毫升的水的体积。

A．三十多 B．四十多 C．五十多 D．六十多
四、巧思妙想算一算。（共8分）
21．(本题8分)求下面图形的表面积和体积。（单位：cm）



五、解决问题。（共32分）
22．(本题4分)做一个无盖的长方体铁桶，共用铁皮192平方分米。已知桶底是边长10分米的正方形，请问桶高几分米？



23．(本题5分)有一个花坛，高0.6米，底面是边长为1.5米的正方形。四周用砖砌成，砖墙的厚度是0.2米，中间填满泥土。需要泥土多少立方米？



24．(本题5分)如图所示，甲是空的长方体容器，乙长方体容器中水深30厘米，要将容器乙中的水倒一部分给容器甲，使两个长方体容器中水的高度相同，这时水深多少厘米？


25．(本题6分)一块长方形铁皮（如下图），从四个角各切掉一个边长5厘米的正方形后，沿虚线折起来，做成一个无盖的铁盒。

（1）这个铁盒用了多少平方厘米的铁皮？
（2）这个铁盒的容积是多少？（厚度忽略不计）




26．(本题6分)商店用一种长方体纸箱装饼干，纸箱从里面测量长是48厘米，宽是24厘米，高是14厘米。饼干包装盒从外面测量是一个长8厘米，宽8厘米，高3厘米的小长方体。
（1）做这个纸箱需要多少平方厘米的硬纸板？
（2）这个纸箱最多能装多少盒饼干？请简要说出怎样摆放？




27．(本题6分)启启用一个长为8厘米，宽为7厘米，高为6厘米的长方体玻璃容器做实验。他先往容器中倒入5厘米深的水，再把一块棱长4厘米的正方体铁块放入水中，水会不会溢出来？
（1）你的判断结果是（        ）。（填“会”或“不会”）
（2）请你用算式表示出你的判断的理由。






























答案解析部分
一、知识空格填一填。
1．2
【分析】长方体底面是长方形，根据长方形的长＝面积÷宽，求出长方体的长，长方体侧面展开是一个大长方形，大长方形的长＝长方体底面周长，大长方形的宽＝长方体的高，表面积－底面积×2＝前后左右4个面的面积和，再除以底面周长就是长方体的高。
【详解】12÷3＝4（厘米）
（4＋3）×2
＝7×2
＝14（厘米）
（52－12×2）÷14
＝（52－24）÷14
＝28÷14
＝2（厘米）
【点睛】关键是熟悉长方体特征，掌握长方体表面积的求法。
2．168
【分析】假设长宽高分别为a，b，h，可得：a×b＝56cm2，a×h＝24cm2，b×h＝21cm2；再根据“长方体的体积＝长×宽×高”进行解答即可。
【详解】假设长宽高分别为a，b，h，
由分析知：a×b＝56cm2，a×h＝24cm2，b×h＝21cm2；
a×b×（a×h）×（b×h）＝56×24×21
a2×b2×h2＝7×8×3×8×3×7
（a×b×h）2＝72×82×32
（a×b×h）2＝（7×8×3）2
a×b×h＝7×8×3
a×b×h＝168（cm3）即长方体的体积是168cm3。
【点睛】解答此题的关键是先分别设出长、宽、高，进而根据题意，根据长方体的体积计算方法列出式子，进行解答即可。
3．1.2
【分析】根据题意，把长方体方钢截成三段，要截2次；每截一次增加2个截面，截2次增加4个截面，表面积会增加4个截面的面积；先用增加的表面积除以4，求出一个截面的面积，再根据长方体的体积公式V＝Sh，求出原来方钢的体积。注意单位的换算：1m2＝100dm2。
【详解】80dm2＝0.8m2
0.8÷4＝0.2（m2）
0.2×6＝1.2（m3）
【点睛】掌握长方体切割的特点，明确表面积增加的是哪些面的面积，以此为突破口，利用公式列式计算。
4．54
【分析】把一个棱长是3米的正方体木块锯成体积相等的8个小正方体，要沿着长、宽、高各切1次，共3次，增加了6个面；每个面的面积是（3×3）平方米，再乘6即可求出增加的表面积。
【详解】2×3＝6（个）
3×3×6
＝9×6
＝54（平方米）
【点睛】本题考查立体图形的切割，明确切一刀增加2个面，进而得出切3刀增加6个面。
5．     36     36     296
【分析】已知长方体的三个面的面积，根据长方体的特征可知，这三个面的面积分别是长×宽、长×高、宽×高；把三个面的面积分解成两数相乘的形式，找出长方体的长、宽、高；
要在它的四周刷上油漆，即在长方体的前后面、左右面共4个面刷油漆，根据“长×高×2＋宽×高×2”代入数据计算，即可求出至少要刷油漆的面积；
根据长方体的体积（容积）＝长×宽×高，求出这个储藏室容积；
根据长方体的特征可知，长方体的底面是一个长方形，已知每个礼盒的底面周长是108cm，即2条长与2条宽的和是108cm；根据长方体的棱长总和＝（长＋宽＋高）×4可知，这个礼盒的棱长总和＝底面周长×2＋高×4，代入数据计算即可。
【详解】18＝6×3
12＝6×2
6＝3×2
所以这个长方体的长是6m，宽是3m，高是2m；
长方体的四周刷上油漆，至少要刷：
6×2×2＋3×2×2
＝12×2＋6×2
＝24＋12
＝36（m2）
这个储藏室容积：
6×3×2
＝18×2
＝36（m3）
每个礼盒的棱长总和：
108×2＋20×4
＝216＋80
＝296（cm）
【点睛】本题考查长方体的表面积、体积（容积）、棱长总和公式的灵活运用，根据长方体的特征，结合三个面的面积找出这个长方体的长、宽、高是解题的关键。
6．     24     8     6     4     4     96
【分析】根据正方体的表面积＝棱长×棱长×6，正方体的体积＝棱长×棱长×棱长；代入数据计算求出正方体的表面积和体积；
用12个这样的正方体，拼成不同形状的长方体，要使拼成长方体的表面积最少，那么正方体重合的面要最多；
因为12＝12×1×1＝4×3×1＝6×2×1＝3×2×2，所以可以拼成四种不同形状的长方体，其中拼成3×2×2减少的面最多，拼成的长方体的表面积最小，即拼成长方体的长是（2×3）cm、宽是（2×2）cm、高是（2×2）cm；
长方体是由12个相同的正方体拼成，用一个正方体的体积乘12，即是拼成的长方体的体积。
【详解】正方体的表面积：
2×2×6
＝4×6
＝24（cm2）
正方体的体积：
2×2×2
＝4×2
＝8（cm3）
拼成长方体的长：2×3＝6（cm）（答案不唯一）
长方体的宽：2×2＝4（cm）（答案不唯一）
长方体的高：2×2＝4（cm）（答案不唯一）
长方体的体积：8×12＝96（cm3）
【点睛】本题考查正方体表面积、体积公式的应用以及立体图形的拼接，掌握正方体拼成长方体的方法，将12分解成3个整数相乘的形式，能很快地找到表面积最少的长方体的拼法。
7．     512     376
【分析】根据正方体的体积＝棱长×棱长×棱长，代入数据计算求出正方体的体积；
根据题意，用一根铁丝围成正方体，那么铁丝的长度等于正方体的棱长总和；根据正方体的棱长总和＝棱长×12，求出铁丝的长度；
这根铁丝又围成了长方体，那么铁丝的长度等于长方体的棱长总和；根据长方体的棱长总和＝（长＋宽＋高）×4可知，长方体的高＝棱长总和÷4－长－宽，即可求出长方体的高；
最后根据长方体的表面积＝（长×宽＋长×高＋宽×高）×2，代入数据计算求出围成的长方体的表面积。
【详解】正方体的体积：
8×8×8
＝64×8
＝512（cm3）
正方体的棱长总和：
8×12＝96（cm）
长方体的高：
96÷4－10－8
＝24－10－8
＝6（cm）
长方体的表面积：
（10×8＋10×6＋8×6）×2
＝（80＋60＋48）×2
＝188×2
＝376（cm2）
【点睛】掌握正方体、长方体的棱长总和、体积公式以及长方体的表面积公式是解题的关键。
8．     30     17
【分析】从正面、后面、左面、右面、上面这五个方向看，都看到的是6个小正方形，那么这个图形所看到的小正方形共有（6×5）个；根据正方形的面积＝边长×边长，求出一个小正方形的面积，再乘小正方形的个数，即是这个图形的所看到的面积的和；
先数出这个几何体原有小正方体的个数，然后将这个几何体补成一个正方体，正方体的每条棱长至少要放3个小正方体，根据正方体的体积＝棱长×棱长×棱长，求出补成的正方体所需小正方体的总个数，再减去原有小正方体的个数，即是至少要添上的小正方体的个数。
【详解】（1）看到小正方形的个数：6×5＝30（个）
所看到图形的面积的和：1×1×30＝30（平方厘米）
（2）原有小正方体个数：
3＋2×2＋1×3
＝3＋4＋3
＝10（个）
补成正方体所需的小正方体总个数：
3×3×3
＝9×3
＝27（个）
至少要添上小正方体：
27－10＝17（个）
【点睛】掌握不规则几何体的表面积、体积的计算方法是解题的关键。
9．     8     38
【分析】在这个长方体中切下一个最大的正方体，正方体的棱长等于长方体的宽，根据正方体的体积公式：V＝a3，把数据代入公式求出它的体积即可；因为正方体的棱长与长方体的宽相同，所以剩余部分表面积最小应该是在两端锯出正方体， 所以此时表面积减少了2个正方体的面。
【详解】2×2×2＝8（dm3）
（4×2＋4×2.5＋2×2.5）×2－2×2×2
＝（8＋10＋5）×2－8
＝23×2－8
＝46－8
＝38（dm2）
【点睛】此题的解题关键是掌握立体图形的切拼方法，灵活运用正方体的体积和长方体的表面积公式，难点在于锯这个正方体的方式有多种，需考虑不同的情况对剩余部分表面积的影响。
10．504
【分析】截去一个高8cm的长方体后，表面积减少的是长方体4个侧面的面积，用192除以4即可计算出1个面的面积为48cm2，根据长方形的面积公式，48除以8即可计算出长方形的宽为6cm，即正方体的棱长。所以原来长方体的长和宽都为6cm，高为（6＋8）cm，利用长方体的体积公式即可得解。
【详解】192÷4÷8
＝48÷8
＝6（cm）
6×6×（6＋8）
＝36×14
＝504（cm3）
【点睛】此题的解题关键是掌握立体图形切拼后表面积的变化情况，灵活运用长方体的体积公式求解。
二、是非曲直辩一辩。
11．×
【分析】本题要把10立方厘米转化为立方米，是小单位变成大单位，要除以进率1000000，据此解答。
【详解】10立方厘米＝10÷1000000＝0.00001（立方米）
10＋0.00001＝10.00001（立方米）
故原题说法错误。
【点睛】明确立方厘米和立方米之间的进率是1000000，是解答此题的关键。
12．√
【详解】略
13．√
【分析】画图，从长方体的一个顶点处切去一个小正方体后，少了一部分，体积肯定是减少的，求表面积的话，可以画出现在这个图形的三视图，三视图的面积之和是不变的，所以表面积也是不变的。
【详解】如图所示：


从长方体的一个顶点处切去一个小正方体后，它的表面积不变，体积减少，题干阐述正确。
故答案为：√
【点睛】从顶点处切，表面积不变，从棱上切，表面积增加两个小正方体的面，从面上切，表面积增加4个小正方体的面。
14．×
【分析】根据长方体的特征和长方体体积的计算方法，由题意知：把一块不规则的橡皮泥捏成长方体形状（均为实心），橡皮泥的形状改变了，体积没有发生改变。
【详解】把一块不规则的橡皮泥捏成长方体形状（均为实心），橡皮泥的形状改变了，体积没有发生改变。
故答案是：×
【点睛】能理解把不规则物体捏成长方体（均为实心），形状改变了，体积没有改变，是解决此题的关键。
15．√
【分析】首先根据长方体的表面积＝（长×宽＋长×高＋宽×高）×2，如果长方体的长、宽、高都扩大到原来的2倍，则长×宽、长×高、宽×高都扩大到原来的4倍，所以表面积扩大为原来的4倍；然后根据长方体的体积＝长×宽×高，如果长方体的长、宽、高都扩大到原来的2倍，则长×宽×高扩大到原来的8倍，所以体积扩大为原来的8倍。
【详解】可以先假设原长方体的长、宽、高分别是a、b、h，则表面积，体积。长方体的长、宽、高都扩大到原来的2倍后，分别是、、，则表面积，体积。
故判断正确。
【点睛】此题主要考查了长方体的体积、长方体的表面积的求法，要熟练掌握，解答此题的关键是要明确：长方体的长、宽、高都扩大到原来的n倍，那么表面积扩大为原来的n2倍，体积扩大为原来的n3倍。
三、众说纷纭选一选。
16．A
【分析】利用长方体的体积公式：V＝abh，代入长、宽和体积的数据，求出长方体包装盒的高度，然后再用长方体的长、宽、高分别与玻璃器皿的长、宽、高相比较，如果玻璃器皿的长、宽、高都小于的长方体的长、宽、高，那么这个玻璃器皿就装的下。要注意可调整玻璃器皿的方向；据此判断。
【详解】15dm3＝15000cm3
15000÷30÷20＝25（cm）
①24＜30，15＜20，30＞25
玻璃器皿的高度比长方体包装盒的高要长，按情况①是装不下的。
②换一个方向放玻璃器皿，把玻璃器皿的高当作长，宽还是宽，长当作高放下去，再比较大小：30＝30，15＜20，24＜25
按情况②，玻璃器皿的长、宽、高都小于的长方体的长、宽、高，所以装得下。
综上，这个玻璃器皿能装下。
故答案为：A
【点睛】此题的解题关键是根据长方体的特征来判断能否装下玻璃器皿，同时还要掌握长方体的体积计算方法。
17．C
【分析】长方体或正方体展开图共四种类型，分别是1－4－1型、2－3－1型、2－2－2型、3－3型，展开图中出现“田”、“凹”、“L”形，不折叠成正方形或长方形。据此解答。
【详解】第一幅平面图形中，有“凹”形，不能折叠成正方形，其余三幅图都是1－4－1形，可以折成长方形或正方形。
故答案为：C
【点睛】本题考查了几何体的展开图，熟记长方体和正方体的展开图的各种情形是解答本题的关键。
18．B
【分析】一个横截面是正方形的长方体，它可以分割成两个同样的正方体，说明前后上下四个面每个面的面积是横截面的2倍，则长方体的表面积是一个横截面面积的10倍，则每个横截面的面积是16平方厘米，一个小正方体有6个面积是16平方厘米的面，据此解答即可。
【详解】根据分析可得：
160÷10×6
＝16×6
＝96（平方厘米）
故答案为：B。
【点睛】本题考查长方体、正方体的表面积，解答本题的关键是掌握长方体的特征。
19．D
【分析】观察图形可知，图中的长方体由12个小正方体组成，分为前后两排，前排的6个小正方体是由第二部分的4个小正方体和第一部分中的2个小正方体组成，第三部分和第一部分剩下的2个小正方体组成后面一排，观察图形可知，第一部分的4个小正方体分别放在前排最右边一列和后排的下层的中间和最右边，所以第三部分的4个小正方体分别在后排的上面一层（有3个）和后排下层的最左边，图形如下：。
【详解】根据分析可知，第三部分所对应的几何体应是：。
故答案为：D
【点睛】认真观察，找出各个部分所在的位置，是解答此题的关键。
20．B
【分析】要求每个铁球的体积在哪一个范围内，根据题意，先求出5个铁球的体积最少是多少，5个铁球的体积要大于（500－300）立方厘米，进而推测这样一个铁球的体积的范围即可。
【详解】因为把5个铁球放入水中，结果水满溢出，
所以5个铁球的体积要大于：500－300＝200（立方厘米）
一个铁球的体积要大于：200÷5＝40（立方厘米）
因此推得这样一个铁球的体积在40立方厘米以上，50立方厘米以下。
故答案为：B
【点睛】此题考查了探索某些实物体积的测量方法，本题关键是明白：杯子里水上升的体积就是5个铁球的体积，进而得解
四、巧思妙想算一算。
21．表面积168cm2；体积112cm3
【分析】从图中可知，左边是正方体，右边是长方体，正方体和长方体有重合部分；把长方体的右面平移到重合处，补给正方体的右面，这样正方体的表面积是6个面的面积之和，长方体的表面积只有上下面、前后面共4个面的面积之和；
图形的表面积＝正方体的表面积＋长方体4个面的面积；根据正方体的表面积＝棱长×棱长×6，长方体的4个面的面积＝长×宽×2＋长×高×2，代入数据计算即可。
图形的体积＝正方体的体积＋长方体的体积，根据正方体的体积＝棱长×棱长×棱长，长方体的体积＝长×宽×高，代入数据计算即可。
【详解】图形的表面积：
4×4×6
＝16×6
＝96（cm2）
6×4×2＋6×2×2
＝24×2＋12×2
＝48＋24
＝72（cm2）
96＋72＝168（cm2）
图形的体积：
4×4×4
＝16×4
＝64（cm3）
6×4×2
＝24×2
＝48（cm3）
64＋48＝112（cm3）
五、解决问题。
22．2.3分米
【分析】铁皮面积－底面积＝前后左右4个面的面积和，将前后左右4个面展开是长方形，长方形的宽就是长方体的高，长方体的长是长方体底面周长，用前后左右4个面的面积和÷底面周长＝长方体的高，据此分析。
【详解】（192－10×10）÷（10×4）
＝（192－100）÷40
＝92÷40
＝2.3（分米）
答：桶高2.3分米。
【点睛】关键是熟悉长方体特征，能想明白无盖长方体铁通展开的形状。
23．0.726立方米
【分析】求需要泥土的体积，就是求长方体花坛的容积。因为花坛的底面是边长为1.5米的正方形，四周用砖砌成，砖墙的厚度是0.2米，那么花坛里面的边长是（1.5－0.2×2）米，根据正方形的面积S＝a2，求出花坛的底面积；然后根据长方体的体积（容积）V＝Sh，即可求解。
【详解】1.5－0.2×2
＝1.5－0.4
＝1.1（米）
1.1×1.1×0.6
＝1.21×0.6
＝0.726（立方米）
答：需要泥土0.726立方米。
【点睛】本题考查长方体体积（容积）公式的运用，关键是理解花坛里面的边长要减去2个砖墙的厚度。
24．10厘米
【分析】根据题干分析可得，可设两个容器的水深相同为x厘米，根据长方体的体积公式可知，甲容器中的水的体积是：50×40×x立方厘米；乙容器中的水的体积是40×25×x立方厘米，根据两个容器内水的体积之和等于乙容器中高为30厘米时的水的体积，即可列出方程，求出x的值即可解答问题。
【详解】解：设两个容器的水深相同为x厘米，根据题意可得方程：
50×40×x＋40×25×x＝40×25×30
2000x＋1000x＝30000
3000x＝30000
x＝30000÷3000
x＝10
答：这时两个容器水深是10厘米。
【点睛】此题考查了长方体的体积公式的计算应用，抓住水的体积不变列出方程解决问题。
25．（1）500平方厘米；（2）1000立方厘米
【分析】（1）从图中可知，用长30厘米、宽20厘米的长方形的面积减去4个边长5厘米的正方形的面积，就是这个铁盒用的铁皮的面积。根据长方形的面积＝长×宽，正方形的面积＝边长×边长，代入数据计算即可。
（2）这个长方体铁盒的长是（30－5×2）厘米，宽是（20－5×2）厘米，高是5厘米，根据长方体的体积（容积）＝长×宽×高，代入数据计算求出这个铁盒的容积。
【详解】（1）30×20－5×5×4
＝600－100
＝500（平方厘米）
答：这个铁盒用了500平方厘米的铁皮。
（2）长方体的长：
30－5×2
＝30－10
＝20（厘米）
长方体的宽：
20－5×2
＝20－10
＝10（厘米）
长方体的容积：
20×10×5
＝200×5
＝1000（立方厘米）
答：这个铁盒的容积是1000立方厘米。
【点睛】（1）理解长方体的表面积就是长方形的面积减去四个小正方形的面积；
（2）关键是找出长方体的长、宽、高，然后运用长方体的体积（容积）公式，列式计算。
26．（1）4320平方厘米；
（2）84盒；先把饼干横着摆2层，再竖着摆1层
【分析】（1）根据长方体表面积公式：S长方体＝（长×宽＋宽×高＋长×高）×2，代入数据计算即可；
（2）结合题目里的数据，可试着先把饼干盒平放，长8厘米对应纸箱的长48厘米、宽8厘米对应纸箱的宽24厘米、高3厘米对应纸箱的高14厘米；14－3×2＝8（厘米），这样一来，在摆完两层后，能发现纸箱剩下的高恰好能对应饼干盒的长和宽，所以就可以把饼干盒竖起来摆放，就是把饼干盒的宽8厘米对应纸箱的高8厘米；①可以把饼干盒的长8厘米对应纸箱的长48厘米、高3厘米对应纸箱的宽24厘米，②也可以把饼干盒的高3厘米对应纸箱的长48厘米、长8厘米对应纸箱的宽24厘米；这样能充分利用空间。
【详解】（1）（24×48＋48×14＋24×14）×2
＝（1152＋672＋336）×2
＝2160×2
＝4320（平方厘米）
答：做这个纸箱需要4320平方厘米的硬纸板。
（2）先横着摆两层
（48÷8）×（24÷8）×2
＝6×3×2
＝36（盒）
14－3×2
＝14－6
＝8（厘米）
再竖着摆一层
（48÷3）×（24÷8）×（8÷8）
＝16×3×1
＝48（盒）
36＋48＝84（盒）
答：这个纸箱最多能装84盒饼干。先把饼干横着摆2层，再竖着摆1层，正好摆满。
【点睛】最后一问充分考查了空间想象能力，可结合画图法，在纸上分析、推理、计算得出结论；能够体会到要结合实际数据来灵活处理问题的方法。
27．（1）会
（2）见详解
【分析】先根据正方体的体积＝棱长×棱长×棱长，求出正方体铁块的体积；已知长方体玻璃容器高为6厘米，水深5厘米，还有（6－5）厘米的无水部分，根据长方体的体积＝长×宽×高，求出无水部分的体积；然后把铁块的体积与无水部分的体积进行比较，如果铁块的体积大于玻璃容器内无水部分的体积，水就会溢出，否则水不会溢出。
【详解】（1）我的判断结果是：会。
（2）正方体的体积：
4×4×4
＝16×4
＝64（立方厘米）
长方体玻璃容器无水部分的体积：
8×7×（6－5）
＝8×7×1
＝56（立方厘米）
64＞56
答：水会溢出来。
【点睛】本题考查正方体、长方体体积计算公式的灵活运用，也可以用正方体铁块的体积除以容器的底面积，求出水面上升的高度，与容器内无水部分的高度相比较，得出结论。