






人教版八年级下册19.2.2 一次函数复习课件ppt
展开(一)能根据函数解析式与图象的关系,判断点是否在函数图象上,求图象上点的坐标。
(二)知道k、b与一次函数图象、性质的关系,能用待定系数法求一次函数解析式.
(三)会利用一次函数与方程(组)、不等式的关系,数形结合的发现方程(组)的解、不等式的解集.
(四)能从函数图象中获取信息,解决有关实际问题;会用函数表示实际问题中变量的关系,并能解决简单实际问题。
一.常量、变量: 在一个变化过程中,数值发生变化的量叫做 ;数值始终不变的量叫做 ;
函数的定义:一般的,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
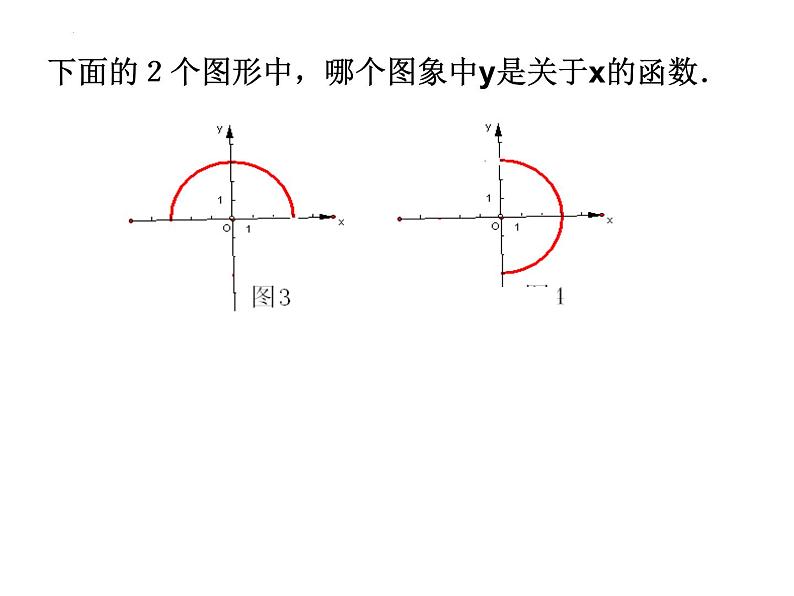
下面的2个图形中,哪个图象中y是关于x的函数.
三、正比例函数与一次函数的概念:
一般地,形如y=kx(k为常数,且k≠0)的函数叫做正比例函数.其中k叫做比例系数。
当b=0 时,y=kx+b 即为 y=kx,所以正比例函数,是一次函数的特例.
一般地,形如y=kx+b(k,b为常数,且k≠0)的函数叫做一次函数.
(1)图象:正比例函数y= kx (k 是常数,k≠0)) 的图象是经过原点的一条直线,我们称它为直线y= kx 。 (2)性质:当k>0时,直线y= kx经过第一,三象限,从左向右上升,即随着x的增大y也增大;当k<0时,直线y= kx经过二,四象限,从左向右下降,即随着 x的增大y反而减小。
四.正比例函数的图象与性质:
五、一次函数与正比例函数的图象与性质
1、图象是经过(0,0)与(1,k)的一条直线
2、当k>0时,图象过一、三象限;y随x的增大而增大。 当k<0时,图象过二、四象限;y随x的增大而减少。
1.已知一次函数y=kx+b的图像如图所示,则A.k>0,b>0 B.k>0,b<0C.k<0,b<0 D.k<0,b>0
2.已知一次函数y=(m-3)x+m-1(1)若此函数图象经过第一、二、三象限,求m的取值范围;(2)当m为何值时,y随x的增大而减小?(3)若函数图象与y轴交点的纵坐标为-2,且图象经过点 A(2,a)、B(-1,b),请你判断a、b的大小关系,并说明理由.
复习检测一(15分钟)
解:(1)由题意得m-3<0 且m+1>0 解得-1
知道直线上下平移的一般性规律
4.一次函数y=kx+b的图象平行于直线y=-2x+1,且与y轴交于点(0,-3),则所一次函数的解析式为 .
5.如图,直线AC经过点A(2,4),与x轴、y轴分别交于点C、点B,点C的横坐标为-4.求:(1)求直线AC的解析式;(2)△ABO的面积.
6.若直线y=kx+6与两坐标轴所围成的三角形面积是24,求直线解析式.
一次函数与一元一次方程:
求ax+b=0(a,b是 常数,a≠0)的解.
x为何值时函数y= ax+b的值为0.
求ax+b=0(a, b是 常数,a≠0)的解.
求直线y= ax+b与 x 轴交点的横坐标.
一次函数与一元一次不等式:
解不等式ax+b>0(a,b是常数,a≠0) .
x为何值时 函数y= ax+b的值 大于0.
解不等式ax+b>0(a,b是常数,a≠0) .
求直线y= ax+b在 x轴上方的部分(射线)所对应的的横坐标的取值范围.
例题:根据图像求kx+b<0的解
解:由题意得,x<2.
一次函数与二元一次方程组:
自变量(x)为何值时两个函数的值相等.并求出这个函数值
确定两直线交点的坐标.
例.如图,一次函数y=kx+b与一次函数y=mx+n的图象相交于点(3,1).
(1)方程组 的解是 .
解:由图可知,当x<3时,mx+n>kx+b
复习检测二(10分钟)
1.骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶.下面是行驶路程s(米)关于时间t(分)的函数图象,那么符合这个同学行驶情况的图象大致是
2、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱。(2)服药5时,血液中含药量为每毫升____毫克。(3)当x≤2时y与x之间的函数关系式是___________。(4)当x≥2时y与x之间的函数关系式是__________
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是___时。
1、下列各坐标系中的曲线中,表示y 是x 的函数的是( ).
2.把直线 向下平移3个单位长度后所得直线解析式为______.
注意:(1)求出函数关系式时,必须找出自变量的取值范围。 (2)画函数图象时,应根据函数自变量的取值范围来确定图象的范围。
图象是包括两端点的线段
3、柴油机在工作时油箱中的余油量Q(千克)与工作时间t(小时)成一次函数关系,当工作开始时油箱中有油40千克,工作3.5小时后,油箱中余油22.5千克(1)写出余油量Q与时间t的函数关系式.
(2)画出这个函数的图象。
人教版八年级下册19.2.2 一次函数评课ppt课件: 这是一份人教版八年级下册19.2.2 一次函数评课ppt课件,共22页。PPT课件主要包含了导入新课,讲授新课,试一试,1填写下表,拓展探究,课堂练习,课堂小结,布置作业等内容,欢迎下载使用。
初中数学人教版八年级下册19.2.2 一次函数多媒体教学ppt课件: 这是一份初中数学人教版八年级下册19.2.2 一次函数多媒体教学ppt课件,共15页。PPT课件主要包含了情境引入,函数的概念是什么,自主探究,Gh-105,y01x+22,ykx+b,总结提高等内容,欢迎下载使用。
初中人教版19.2.2 一次函数复习ppt课件: 这是一份初中人教版19.2.2 一次函数复习ppt课件,共35页。PPT课件主要包含了学习目标,知识梳理,kx+b,k≠0,重点突破,m2-31,m-2≠0,m±2,m≠2,m-2等内容,欢迎下载使用。













