初中数学7.2.2用坐标表示平移图片ppt课件

这是一份初中数学7.2.2用坐标表示平移图片ppt课件，共34页。PPT课件主要包含了向右平移a个单位后，x+a，向左平移a个单位后，x-a，向上平移b个单位后，y+b，向下平移b个单位后，y-b，-1-4，3-1等内容，欢迎下载使用。

1.掌握平面直角坐标系中的点或图形平移引起的点的坐标的变化规律; (重点、难点)2.体会平面直角坐标系是数与形之间的桥梁，感受代数与几何的相互转化，初步建立空间概念.
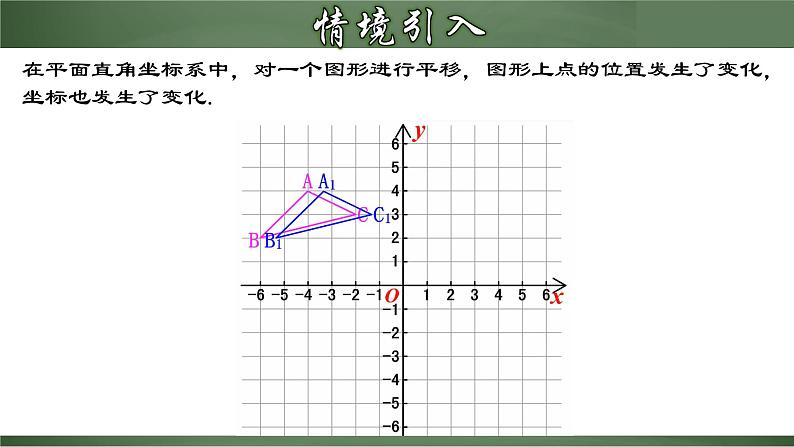
在平面直角坐标系中，对一个图形进行平移，图形上点的位置发生了变化，坐标也发生了变化.
如图，在平面直角坐标系中有A、B、C三点，请你分别将这三点向左、向右、向上、向下平移，观察它们的坐标是否按一定的规律变化呢？
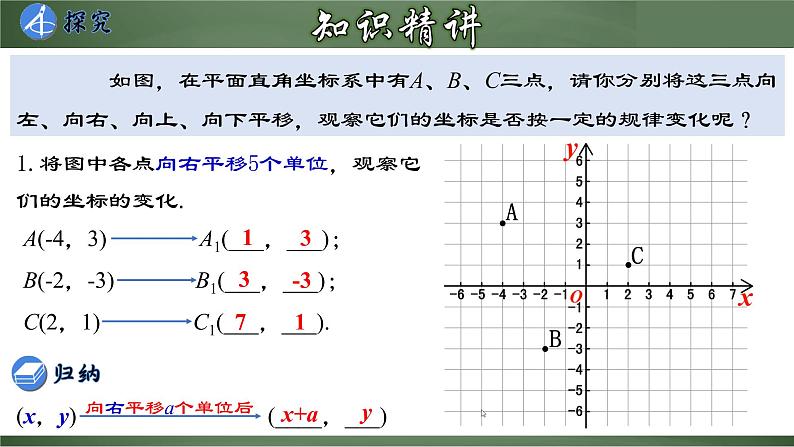
1.将图中各点向右平移5个单位，观察它们的坐标的变化.
A(-4，3) A1(___，___)；B(-2，-3) B1(___，___)；C(2，1) C1(___，___).
(x，y) (____，___)
2.将图中各点向左平移2个单位，观察它们的坐标的变化.
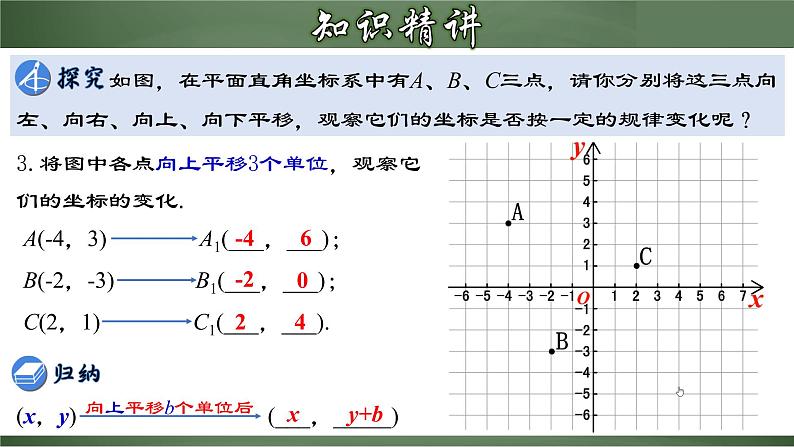
3.将图中各点向上平移3个单位，观察它们的坐标的变化.
(x，y) (___，_____)
4.将图中各点向下平移2个单位，观察它们的坐标的变化.
一般地，在平面直角坐标系中，将点(x，y) 向右(或左)平移a个单位长度，可以得到对应点(____，____)(或(____，____))；将点(x，y)向上(或下)平移b个单位长度，可以得到对应点(____，____)(或(____，____)).
左右移动改变点的横坐标，左减右加；上下移动改变点的纵坐标，下减上加．
向左平移a个单位对应点P2(x-a,y)
向右平移a个单位对应点 P1(x+a,y)
向上平移b个单位对应点P3(x,y+b)
向下平移b个单位对应点P4(x,y-b)
图形上的点P(x,y)
平面直角坐标系内点的坐标平移规律
例1.平面直角坐标系中,将点A(－3，－5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为(　　) A.(1,－8) B.(1,－2) C.(－6,－1) D.(0,－1)
【分析】点A的坐标为(－3,－5)，将点A向上平移4个单位，再向左平移3个单位到点B，点B的横坐标是－3－3＝－6，纵坐标为－5＋4＝－1，即(－6,－1)．
【分析】将点P（﹣2，1）向右平移4个单位长度，再向上平移3个单位长度得到点P′ 的坐标是（﹣2+4，1+3），即（2，4）．
如图，正方形ABCD四个顶点的坐标分别是A(-2，4)，B(-2，3)，C(-1，3)，D(-1，4)，将正方形ABCD向下平移7个单位长度，再向右平移8个单位长度，两次平移后四个顶点相应变为点E，F，G，H，它们的坐标分别是什么？如果直接平移正方形ABCD，使点A移到点E，它和我们前面得到的正方形的位置相同吗？
解：点E，F，G，H的坐标分别是(6，-3)，(6，-4)，(7，-4)，(7，-3).如果直接平移正方形ABCD，使点A移到点E，它和之前得到的正方形的位置相同.
一般地，将一个图形依次沿两个坐标轴方向平移所得到的图形，可以通过将原来的图形作一次平移得到. 对一个图形进行平移，这个图形上所有点的坐标都要发生相应的变化；反过来，从图形上的点的坐标的某种变化，我们也可以看出对这个图形进行怎样的平移.
例3.如图，三角形ABC三个顶点的坐标分别是A(4，3)，B(3，1)，C(1，2). (1)将三角形ABC三个顶点的横坐标都减去6，纵坐标不变，分别得到点A1、B1、C1，依次连接A1、B1、C1，所得三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系？
解：(1)A1(-2，3)，B1(-3，1)，C1(-5，2)，依次连接A1、B1、C1，所得三角形A1B1C1与三角形ABC的大小、形状完全相同，位置不同.
三角形A1B1C1可以看作将三角形ABC向左平移6个单位长度得到.
例3.如图，三角形ABC三个顶点的坐标分别是A(4，3)，B(3，1)，C(1，2). (2)将三角形ABC三个顶点的纵坐标都减去5，横坐标不变，分别得到点A2、B2、C2，依次连接A2、B2、C2，所得三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系？
解:(2)A2(4，-2)，B2(3，-4)，C2(1，-3)，依次连接A2、B2、C2，所得三角形A2B2C2与三角形ABC的大小、形状完全相同，位置不同.
三角形A2B2C2可以看作将三角形ABC向下平移5个单位长度得到.
如图，将平行四边形ABCD向左平移2个单位长度，然后再向上平移3个单位长度，可以得到平行四边形A′B′C′D′，画出平移后的图形，并指出其各个顶点的坐标.
解：如图，平行四边形A′B′C′D′为所求.A′(-3，1)，B′(1，1)，C′(2，4)，D′(-2，4).
(1)如果将这个问题中的“横坐标都减去6”，“纵坐标都减去5”相应地变为“横坐标都加3”，“纵坐标都加2”，分别能得到什么结论？画出得到的图形.
解：(1)A3(7，3),B3(6，1),C3(4，2),依次连接A3、B3、C3,所得三角形A3B3C3与三角形ABC的大小、形状完全相同,位置不同.三角形A3B3C3可以看作将三角形ABC向右平移3个单位长度得到.
A4(4，5),B4(3，3),C4(1，4)，依次连接A4、B4、C4,所得三角形A4B4C4与三角形ABC的大小、形状完全相同,位置不同.三角形A4B4C4可以看作将三角形ABC向上平移2个单位长度得到.
(2)如果将三角形ABC三个顶点的横坐标都减去6，同时纵坐标都减去5，能得到什么结论？画出得到的图形.
(2)A5(-2,-2)，B5(-3,-4)，C5(-5,-3)，依次连接A5、B5、C5，所得三角形A5B5C5与三角形ABC的大小、形状完全相同，位置不同.三角形A5B5C5可以看作将三角形ABC先向左平移6个单位，再向下平移5个单位长度得到.
一般地，在平面直角坐标系内，如果把一个图形各个点的横坐标都加(或减去)一个正数a，相应的新图形就是把原图形向右(或向左)平移a个单位长度；如果把它各个点的纵坐标都加(或减去)一个正数a，相应的新图形就是把原图形向上(或向下)平移a个单位长度.
例4.如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a＋6,b＋2)．(1)请画出上述平移后的三角形A1B1C1，并写出点A、C、A1、C1的坐标；
解:(1)三角形A1B1C1如图所示，各点的坐标分别为A(－3，2)、C(－2，0)、A1(3，4)、C1(4，2)；
(2)求出以A、C、A1、C1为顶点的四边形的面积.
(2)连接AA1,CC1,
例5.如图，A1(1, 0), A2(1，1)，A3(-1, 1)，A4(-1, -1),A5(2，-1),...，则A2018的坐标为__________.
【分析】依题得，A4(-1, -1)，A8(-2，-2)，A12(-3，-3)，…，A2016(-504，-504) ，因此，A2017(505，-504)，所以，A2018(505,505).
3.将某图形的各点的纵坐标减去2，横坐标加上1，可将该图形（     ）A．横向向左平移2个单位，纵向向上平移2个单位B．横向向左平移1个单位，纵向向下平移2个单位C．横向向右平移1个单位，纵向向上平移2个单位D．横向向右平移1个单位，纵向向下平移2个单位
10.如图，三角形ABC是由三角形DEF经过某种变换得到的，观察对应点A与D，B与E,C与F的坐标变化，说明三角形ABC是由三角形DEF经过怎么的变换得到的.
解:三角形ABC可以看作是三角形DEF先向左平移7个单位长度，然后再向上平移3个单位长度得到的;也可以看作是三角形DEF先向.上平移3个单位长度，然后再向左平移7个单位长度得到的.
11.如图，已知单位长度为1的方格中有个三角形ABC.(1)请画出三角形ABC向上平移3格再向右平移2格后所得的三角形A'B'C';(2)请以点A为坐标原点建立平面直角坐标系(在图中画出)，然后写出点B、点B'的坐标.
解:(1)如图三角形A'B'C'为所求;(2)如图，以点A为坐标原点建立平面直角坐标系，可得B(1，2),B′(3，5).
12.如图，A，B两点的坐标分别为(2，3)，(4，1).(1)求三角形ABO的面积;(2)把三角形ABO向下平移3个单位后得到一个新的三角形O'A'B'，求三角形O'A'B'的3个顶点的坐标.