中考数学总复习第四章第19课时图形的相似课件

这是一份中考数学总复习第四章第19课时图形的相似课件，共44页。PPT课件主要包含了大或缩小，答案比值，相似比，答案相等，对应角平分线的比，对应中，线的比，对应周长的比，相似比的平方，答案1两角等内容，欢迎下载使用。

1.了解比例的性质、线段的比、成比例的线段.2.掌握相似图形的性质(相似多边形的对应角相
等，对应边成比例，面积的比等于对应边比的平方).3.了解两个三角形相似的性质定理和判定定理，会
用图形的相似解决一些简单的实际问题.
4.了解图形的位似，能够利用位似将一个图形放
答案：bc2.相似多边形的对应边的________相等，对应角________.如果两个多边形的对应边的比值相等并且对应角相等，那么就称这两个多边形为相似多边形.相似多边形的对应边的比叫作________.
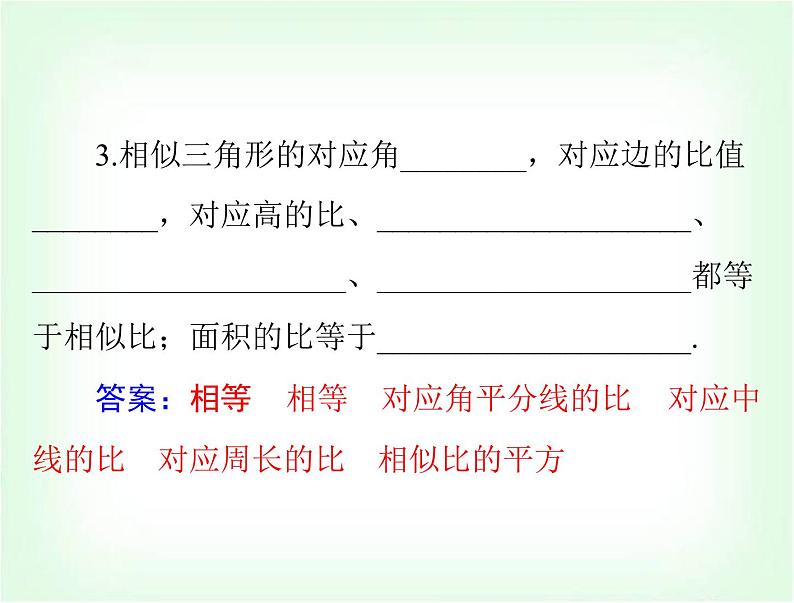
3.相似三角形的对应角________，对应边的比值________，对应高的比、____________________、____________________、____________________都等于相似比；面积的比等于____________________.
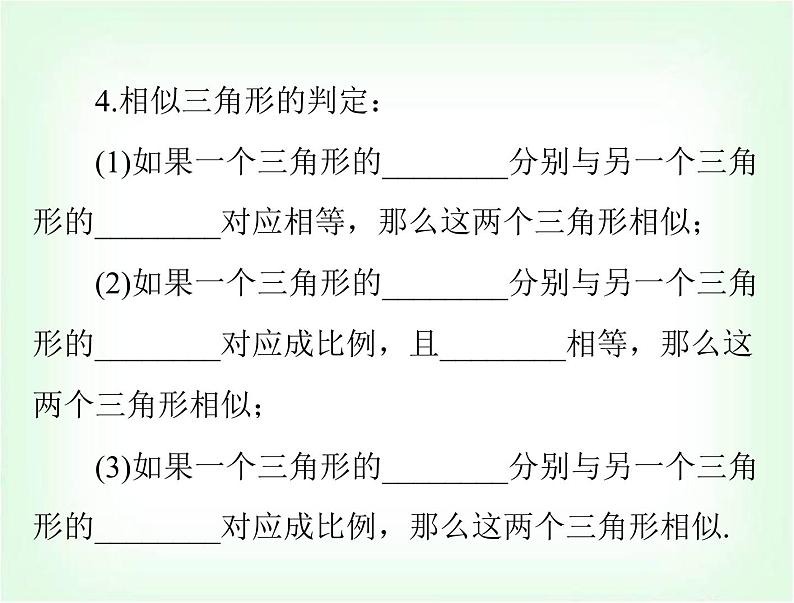
4.相似三角形的判定：
(1)如果一个三角形的________分别与另一个三角形的________对应相等，那么这两个三角形相似；(2)如果一个三角形的________分别与另一个三角形的________对应成比例，且________相等，那么这两个三角形相似；
(3)如果一个三角形的________分别与另一个三角形的________对应成比例，那么这两个三角形相似.
5.如果两个图形不仅是相似图形，而且_____________________________，那么这两个相似图形叫作位似图形，这个点叫作____________，这时的相似比又称为位似比.位似图形上任意一对对应点到位似中心的距离之比等于____________.答案：每组对应点所在直线都过同一个点
2.(2022·临沂)如图，在△ABC 中，DE∥BC，
，若 AC＝6，则 EC＝(
相似三角形的判定3.(1)如图，如果__________，则△ABC∽△ADE.
(2)能说明△ABC∽ △A′B′C′的条件是(
答案：(1)DE∥BC(答案不唯一)
4.(2022·菏泽)如图所示，在 Rt△ABC 中，∠ABC＝90°，E 是边 AC 上一点，且 BE＝BC，过点 A 作BE 的垂线，交 BE 的延长线于点 D，求证：△ADE∽△ABC.
证明：∵BE＝BC，∴∠C＝∠CEB.
∵∠CEB＝∠AED，∴∠C＝∠AED.∵AD⊥BE，
∴∠D＝∠ABC＝90°，∴△ADE∽△ABC.
图形的位似5.(2022·重庆)如图，△ABC 与△DEF 位似，点 O是它们的位似中心，且相似比为 1∶2，则△ABC 与
△DEF 的周长之比是(
1.平行于三角形一边的直线和其他两边相交，所构
成的三角形与原三角形相似.
2.注意证明全等和相似的判定方法的区别和联系.3. 比例式或等积式的证明，一般是把等积式化为比例式，然后由比例式寻找相似三角形.
1.(2022·丽水)如图所示，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点 A，B，C 都在横线上.若线
段 AB＝3，则线段 BC 的长是(
BC＝2，则 EF＝(
3.如图，D 是△ABC 的边 BC 上一点，AB＝4，AD＝2，∠DAC＝∠B，如果△ABD 的面积为 15，那
么△ACD 的面积为(
4.(2020·绍兴)如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为 2∶5，且三角板的一
边长为 8 cm.则投影三角板的对应边长为(
5.(2022·连云港)△ABC 的三边长分别为 2，3，4，另有一个与它相似的△DEF，其最长边为12，则△DEF
6.(2021·淄博)如图，AB，CD 相交于点 E，且AC∥EF∥DB，点 C，F，B 在同一条直线上.已知 AC＝p，EF＝r，DB＝q，则 p，q，
r 之间满足的数量关系式是(
7.在平面直角坐标系中，已知点 E(－4，2)，F(－2，
－2)，以原点 O 为位似中心，相似比为缩小，则点 E 的对应点 E′的坐标是(
B.(－8，4)D.(－2，1)或(2，－1)
A.(－2，1)C.(－8，4)或(8，－4)答案：D
EF＝ AD，则图中阴影部分的面积为(
8.(2020·海南)如图，在矩形 ABCD 中，AB＝6，BC＝10，点 E，F 在 AD 边上，BF 和 CE 交于点 G，若
9.(2022·成都)如图，△ABC 和△DEF 是以点 O 为位似中心的位似图形.若 OA∶AD＝2∶3，则△ABC 与△DEF 的周长比是________.
10.如图，在平面直角坐标系中有两点 A(4，0)，
B(0，2)，如果点 C 在 x 轴上(C 与 A 不重合)，当点 C的坐标为______________时，使得△BOC∽△AOB.
答案：(1，0)或(－1，0)
11.(2021·镇江)如图，点 D，E 分别在△ABC 的边AC，AB 上，△ADE∽△ABC，M，N 分别是 DE，BC
12.(2021·黔东南州)已知在平面直角坐标系中，△AOB 的顶点分别为点 A(2，1)、点 B(2，0)、点 O(0，0)，若以原点 O 为位似中心，相似比为 2，将△AOB 放大，则点 A 的对应点的坐标为____________________.
答案：(4，2)或(－4，－2)
13.(2020·宁夏)如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别是 A(1，3)，B(4，1)，C(1，1).
(1)画出△ABC关于x轴成轴对称的△A1B1C1；(2)画出△ABC 以点 O 为位似中心，位似比为
1∶2的△A2B2C2.
解：(1)如图所示，△A1B1C1 为所求.(2)如图所示，△A2B2C2 为所求.
14.如图，正方形 ABCD 中，M 为 BC 上一点，F
是 AM 的中点，EF⊥AM，垂足为 F，交 AD 的延长线于点 E，交 DC 于点 N.
(1)求证：△ABM∽△EFA；
(2)若 AB＝12，BM＝5，求 DE 的长.
(1)证明：∵四边形 ABCD 是正方形，∴AB＝AD，∠B＝90°，AD∥BC，∴∠AMB＝∠EAF.又∵EF⊥AM，
∴∠AFE＝90°，∴∠B＝∠AFE，∴△ABM∽△EFA.
15.如图，已知 AC，AD 是⊙O 的两条割线，AC
与⊙O 交于 B，C 两点，AD 过圆心 O 且与⊙O 交于 E，D 两点，OB 平分∠AOC.
(1)求证：△ACD∽△ABO；
(2)过点 E 的切线交 AC 于点 F，若 EF∥OC，
(1)证明：∵OB 平分∠AOC，
∴∠D＝∠BOE.又∵∠A＝∠A，∴△ACD∽△ABO.
(2)解：∵EF 切⊙O 于点 E，∴∠OEF＝90°.∵EF∥OC，∴∠DOC＝∠OEF＝90°.∵OC＝OD＝3，
16.如图，正方形ABCD的边长为 4，M，N 分别是BC，CD 上的两个动点，当 M 点在 BC 上运动时，保持 AM 和 MN 垂直.
(1)证明：Rt△ABM∽Rt△MCN；
(2)设 BM＝x，梯形 ABCN 的面积为 y，求 y 与 x
之间的函数关系式；当 M 点运动到什么位置时，四边形 ABCN 面积最大，并求出最大面积；
(3)当 M 点运动到什么位置时，Rt△ABM∽
Rt△AMN，求此时 x 的值.
(1)证明：在正方形 ABCD 中，AB＝BC＝CD＝4，
∵AM⊥MN，∴∠AMN＝90°，∴∠CMN＋∠AMB＝90°.
在 Rt△ABM 中，∠MAB＋∠AMB＝90°，∴∠CMN＝∠MAB，
∴Rt△ABM∽Rt△MCN.