中考数学总复习第四章第21课时解直角三角形的应用课件

这是一份中考数学总复习第四章第21课时解直角三角形的应用课件，共58页。PPT课件主要包含了际问题，答案下往上，水平线，答案上往下，答案方向角，数精确到哪一位，仰角与俯角，答案30°，方位角，A75m等内容，欢迎下载使用。
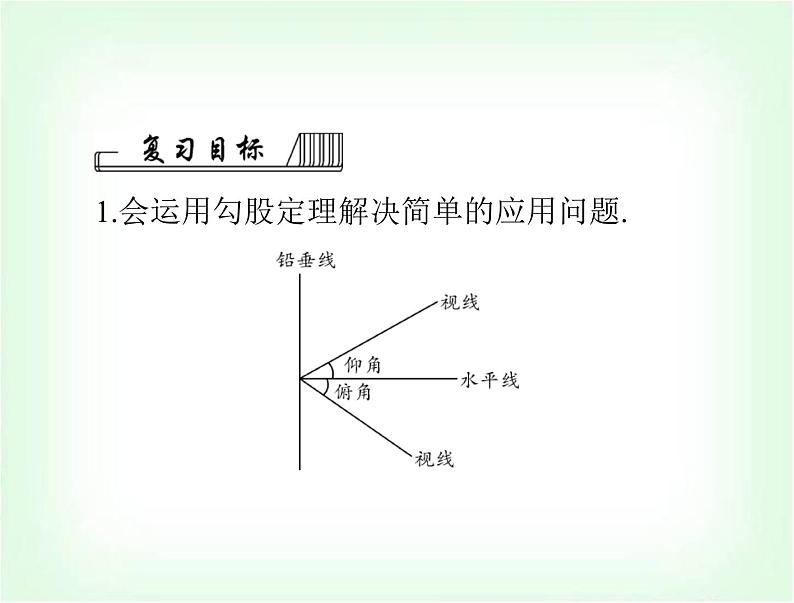
1.会运用勾股定理解决简单的应用问题.
2.运用三角函数解决与直角三角形有关的简单实
3.了解俯角、仰角、方位角、坡角、坡度等概念.4.了解近似数；在解决实际问题中，能用计算器进行近似计算，并按问题的要求对结果取近似值.
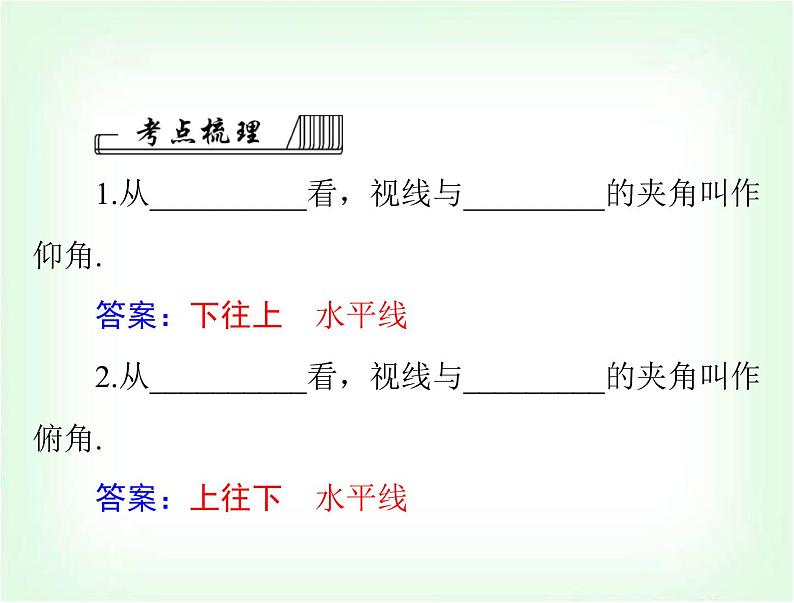
1.从__________看，视线与_________的夹角叫作仰角.
2.从__________看，视线与_________的夹角叫作俯角.
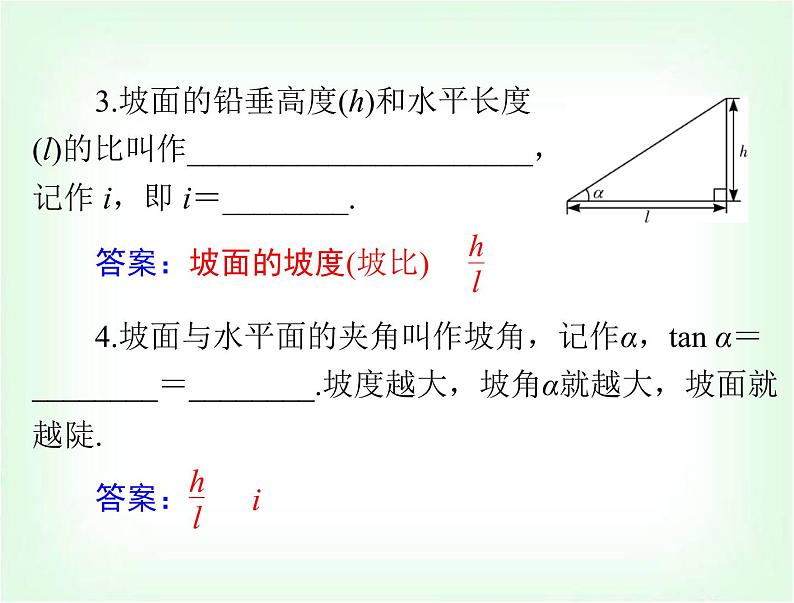
3.坡面的铅垂高度(h)和水平长度(l)的比叫作______________________，记作 i，即 i＝________.
答案：坡面的坡度(坡比)
4.坡面与水平面的夹角叫作坡角，记作α，tan α＝________＝________.坡度越大，坡角α就越大，坡面就越陡.
5.指南或指北的方向线与目标方向线所成的小于
90°的角为________.
6.一个近似数，四舍五入到哪一位，就说这个近似
1.如图，小丽为了测旗杆 AB 的高度，小丽眼睛距地面 1.5 米，小丽站在 C 点，测出旗杆 A 的仰角为30°，小丽向前走了 10 米到达点 E，此时的仰角为60°，求旗杆的高度.
2.如图，一水库迎水坡 AB 的坡度 i＝1∶ 　 ，则
该坡的坡角α＝________.
3.如图，水池的横断面为梯形 ABCD，迎水坡 BC的坡角 B 为 30°，背水坡 AD 的坡度 i＝1∶1.2，坝顶宽 DC＝2.5 m，坝高 CF＝4.5 m.
求：(1)迎水坡 BC 的长；(2)迎水坡 BC 的坡度；
(3)坝底 AB 的长.(结果精确到 0.1)
解：如图，作 DE⊥AB 于点 E，(1)∵ CF＝4.5，∠B＝30°，
4.如图，在一笔直的海岸线上有 A，B 两个观测站，A 在 B 的正西方向，AB＝2 km，从观测站 A 测得船 C在北偏东 45°的方向，从观测站 B 测得船 C 在北偏西30°的方向.求船 C 离观测站 A 的距离.
解：如图，过点 C 作 CD⊥AB 于点 D，则∠CAD＝∠ACD＝45°，∴AD＝CD，
设 AD＝x，则 AC＝ 　x.∴BD＝AB－AD＝2－x，∵∠CBD＝60°，在 Rt△BCD 中，
运用勾股定理和锐角三角函数解决实际问题5.如图，有一斜坡 AB，坡顶 B 离地面的高度 BC
为 30 m，斜坡的倾斜角是∠BAC，若 tan∠BAC＝
则此斜坡的水平距离 AC 为(
6.某市在“旧城改造”中计划在市内一块如图的三角形空地上移植某种草皮以美化环境，已知这种草
皮每平方米售价 a 元，则购买这种草皮至少需要(
B.225a 元D.300a 元
A.450a 元C.150a 元答案：C
与解直角三角形有关的应用问题逐步成为命题的热点，其主要类型有轮船定位问题、堤坝工程问题、建筑测量问题、高度测量问题等，解决各类应用问题时要注意把握各类图形的特征及解法，适当添加辅助线构造直角三角形.
1.(2021·深圳)如图所示，在点 F 处，看建筑物顶端 D 的仰角为 32°，向前走了 15 米到达点 E，即 EF＝15 米，在点 E 处看点 D 的仰角为 64°，则 CD 的高
)B.15tan 64°D.15tan 32°
用三角函数表示为(A.15sin 32°C.15sin 64°答案：C
2.如果三角形满足一个角是另一个角的 3 倍，那么我们称这个三角形为“智慧三角形”.下列各组数据中，
能作为一个智慧三角形三边长的一组是(
3.(2020·黔西南州)如图，某停车场入口的栏杆 AB，从水平位置绕点 O 旋转到 A′B′的位置，已知 AO 的长为 4 米.若栏杆的旋转角∠AOA′＝α，则栏杆 A 端升高
4.(2021·日照)如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔 AB 的高度，他从古塔底部点 B 处前行 30 m 到达斜坡 CE 的底部点 C 处，然后沿斜坡 CE 前行 20 m 到达最佳测量点 D 处，在点D 处测得塔顶 A 的仰角为 30°，已知斜坡的斜面坡度i＝1∶ ，且点 A，B，C，D，E 在同一平面内，小
明同学测得古塔 AB 的高度是(
5.如图，学校环保社成员想测量斜坡 CD 旁一棵树AB 的高度，他们先在点 C 处测得树顶 B 的仰角为60°，然后在坡顶 D 测得树顶 B 的仰角为 30°，已知斜坡 CD 的长度为 20 m，
DE 的长为 10 m，则树AB的高度是(
6.(2021·济南)无人机低空遥感技术已广泛应用于农作物监测.如图，某农业特色品牌示范基地用无人机对一块试验田进行监测作业时，在距地面高度为 135 m的 A 处测得试验田右侧边界 N 处俯角为 43°，无人机垂直下降 40 m 至 B 处，又测得试验田左侧边界 M 处俯角为 35°，则 M，N 之间的距离为(参考数据：tan 43°≈0.9，sin 43°≈0.7，cs 35°≈0.8，
tan 35°≈0.7，结果保留整数)(
7.(2021·玉林)如图，某港口 P 位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行 12 海里和 16 海里，1 小时后两船分别位于点 A，B 处，且相距 20 海里，如果知道甲船沿北偏西 40°方向航行，则乙船沿 ____________________方向航行.
8.如图，某河道要建造一座公路桥，要求桥面离地面高度 AC 为 4 米，引桥的坡角∠ABC 为 15°，则引桥的水平距离 BC 的长是__________米.
9.如图，某渔船在海面上朝正东方向匀速航行，在 A 处观测到灯塔 M 在北偏东 60°方向上，航行半小时后到达 B 处，此时观测到灯塔 M 在北偏东 30°方向上，那么该船继续航行__________分钟可使渔船到达离灯塔距离最近的位置.
10.如图，在小山的东侧 A 点有一个热气球，由于受西风的影响，以 30 米/分的速度沿与地面成 75°角的方向飞行，25 分钟后到达 C 处，此时热气球上的人测得小山西侧 B处的俯角为 30°，则小山东西两侧 A，B 两点间的距离为________米.
11.(2021·包头)某工程队准备从 A 到 B 修建一条隧道，测量员在直线 AB 的同一侧选定 C，D 两个观测点，
C，D 在同一水平面内).(1)求 A，D 两点之间的距离；(2)求隧道 AB 的长度.
解：(1)过点 A 作 AE⊥CD 于点 E，如图所示，
则∠AEC＝∠AED＝90°.∵∠ACD＝60°，
∴∠CAE＝90°－60°＝30°，
12.(2022·广州)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图所示，在某一时刻，旗杆 AB 的影子为 BC，与此同时在 C 处立一根标杆 CD，标杆 CD 的影子为 CE，CD＝1.6 m，BC＝5CD.
(1)求 BC 的长；
(2)从条件①、条件②这两个条件中选择一个作为
已知条件，求旗杆 AB 的高度.
条件①：CE＝1.0 m；条件②：从 D 处看旗杆顶部
A 的仰角α为 54.46°.
注：如果选择条件①和条件②分别作答，按第一
参考数据：sin 54.46°≈0.81，cs 54.46°≈0.58，
tan 54.46°≈1.40.
解：(1)∵BC＝5CD，CD＝1.6 m，∴BC＝5×1.6＝8(m)，∴BC 的长为 8 m.(2)若选择条件①：
∴旗杆 AB 的高度为 12.8 m；若选择条件②：
如图，过点 D 作 DF⊥AB，垂足为 F，
则 DC＝BF＝1.6 m，DF＝BC＝8 m，在 Rt△ADF 中，∠ADF＝54.46°，
∴AF＝DF·tan 54.46°≈8×1.40＝11.2(m)，∴AB＝AF＋BF＝11.2＋1.6＝12.8(m)，∴旗杆 AB 的高度约为 12.8 m.
13.(2020·镇江)如图，点 E 与树 AB 的根部点 A，
建筑物 CD 的底部点 C 在一条直线上，AC＝10 m.小明站在点 E 处观测树顶 B 的仰角为 30°，他从点 E 出发沿 EC 方向前进 6 m 到点 G 时，观测树顶 B 的仰角为45°，此时恰好看不到建筑物 CD 的顶部 D(H，B，D 三点在一条直线上).已知小明的眼睛离地面 1.6 m，求建筑物 CD的高度(结果精确到 0.1 m，参考数据：
解：如图，延长 FH，交 CD 于点 M，交 AB 于
∵∠BHN＝45°，BA⊥MH，则 BN＝NH，
设 BN＝NH＝x.∵HF＝6，∠BFN＝30°，
DM＝MH＝MN＋NH，∵MN＝AC＝10 m，
则 DM＝10＋8.19＝18.19(m)，
∴CD＝DM＋MC＝DM＋EF＝18.19＋1.6＝
19.79(m)，19.79 m≈19.8 m.
答：建筑物 CD 的高度约为 19.8 m.
14.如图，某湖中有一座小岛，湖边有一条笔直的观光小道 AB，现决定从小岛架一座与观光小道垂直的小桥 PD，小张在小道上测得如下数据：AB＝80.0 米，∠PAB ＝38.5°，∠PBA＝26.5°.请帮助小张求出小桥PD 的长并确定小桥在小道上的位置.(以 A，B 为参照点，结果精确到 0.1 米，参考数据：sin 38.5°≈0.62，cs 38.5°≈0.78，tan 38.5°≈
0.80，sin 26.5°≈0.45，cs 26.5°≈0.89，tan 26.5°≈0.50)
解：设 PD＝x 米，∵PD⊥AB，∴∠ADP＝∠BDP＝90°，
又∵AB＝80.0 米，∴1.25x＋2x＝80.0，解得 x≈24.6，即 PD≈24.6 米，∴DB＝2x＝49.2.∴小桥 PD 的长度约为 24.6 米，位于 AB 之间距点 B 约 49.2 米.
15.图 1 是挂墙式淋浴花洒的实物图，图 2 是抽象出来的几何图形.为使身高 175 cm 的人能方便地淋浴，应当使旋转头固定在墙上的某个位置 O，花洒的最高点 B 与人的头顶的铅垂距离为 15 cm，已知龙头手柄OA 长为 10 cm，花洒直径 AB 是 8 cm，龙头手柄与墙面的较小夹角∠COA＝26°，∠OAB＝146°.安装时，旋转头的固定点 O 与地面的距离应为多少？(计算
结果精确到 1 cm，参考数据：sin 26°≈0.44，cs 26°≈0.90，tan 26°≈0.49)
解：如图，过点 B 作地面的垂线，垂足为 D，过点 A 作地面 GD 的平行线，交 OC 于点 E，交 BD 于点 F，
在 Rt△AOE 中，∠AOE＝26°，OA＝10，则 OE＝OA·cs∠AOE≈10×0.90＝9 cm，在 Rt△ABF 中，∠BOF＝146°－90°－26°＝30°，AB＝8，
∴OG＝BD－BF－OE＝(175＋15)－4－9＝177(cm).答：旋转头的固定点 O 与地面的距离应为 177 cm.
16.脱贫攻坚工作让老百姓过上了幸福的生活.图 1是政府给贫困户新建的房屋，图 2 是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高 AB 所在的直线，为了测量房屋的高度，在地面上 C 点测得屋顶 A 的仰角为 35°，此时地面上 C 点，屋檐上 E 点，屋顶上 A 点三点恰好共线，继续向房屋方向走 8 m 到达点 D 时，又测得屋檐 E 点的仰角为 60°，房屋的顶层横梁 EF＝12 m，EF∥CB，AB 交 EF 于点 G(点 C，
D，B 在同一水平线上)(参考数据：sin 35°≈0.6，cs 35°≈0.8，tan 35°≈0.7， ≈1.7).(1)求屋顶到横梁的距离 AG；(2)求房屋的高 AB(结果精确到 1 m).
解：(1)∵房屋的侧面示意图是一个轴对称图形，对称轴是房屋的高 AB 所在的直线，EF∥BC，
EF，∠AEG＝∠ACB＝35°，
在 Rt△AGE 中，∠AGE＝90°，∠AEG＝35°，
∵tan∠AEG＝tan 35°＝
∴AG＝6×0.7＝4.2(m).答：屋顶到横梁的距离 AG 为 4.2 m.
(2)如图，过点 E 作 EH⊥CB 于点 H，
在 Rt△EDH 中，∠EHD＝90°，∠EDH＝60°，