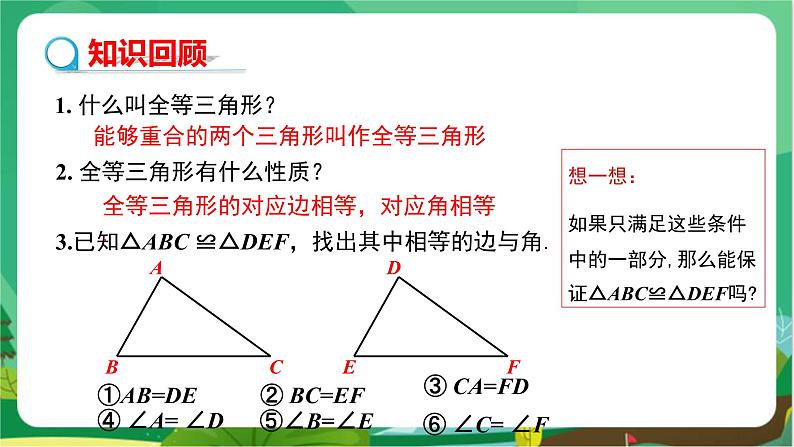
八年级上册第2章 三角形2.5 全等三角形教学课件ppt

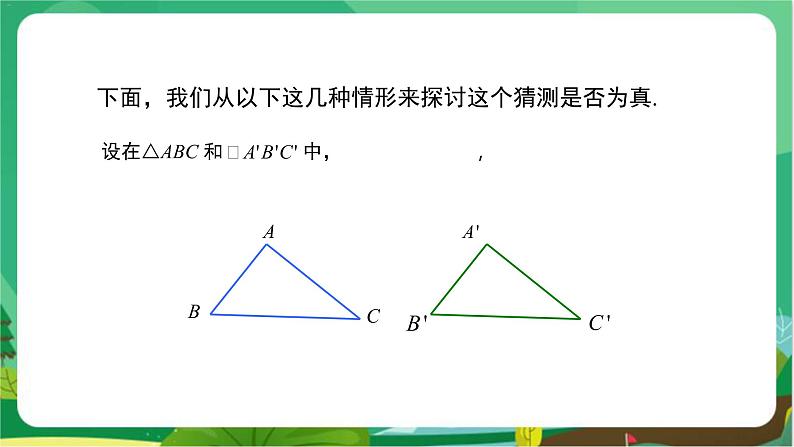
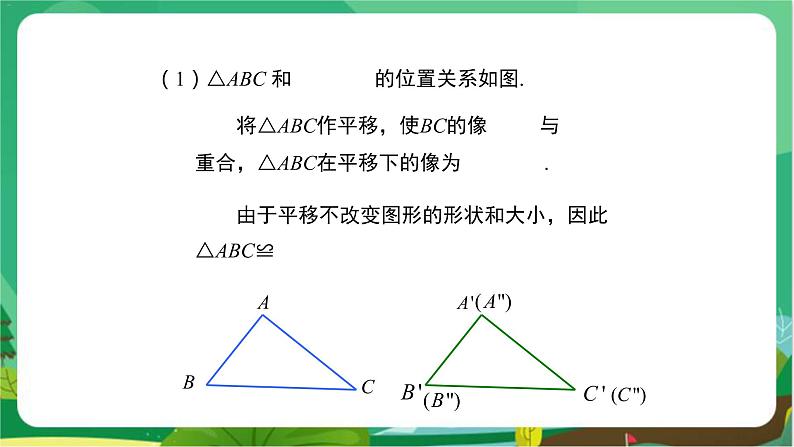
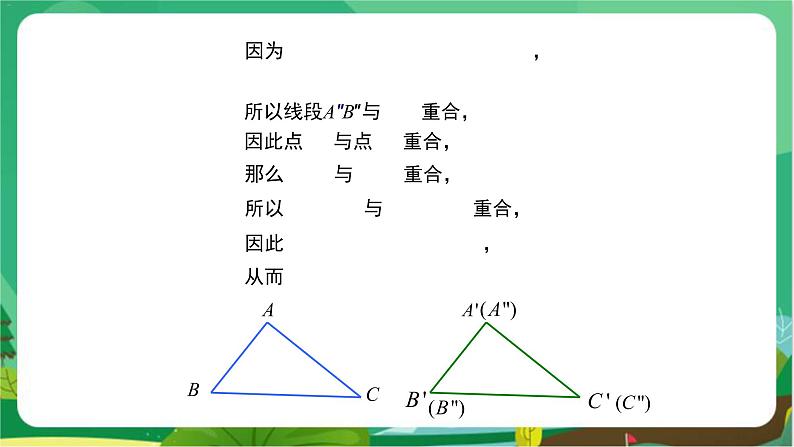
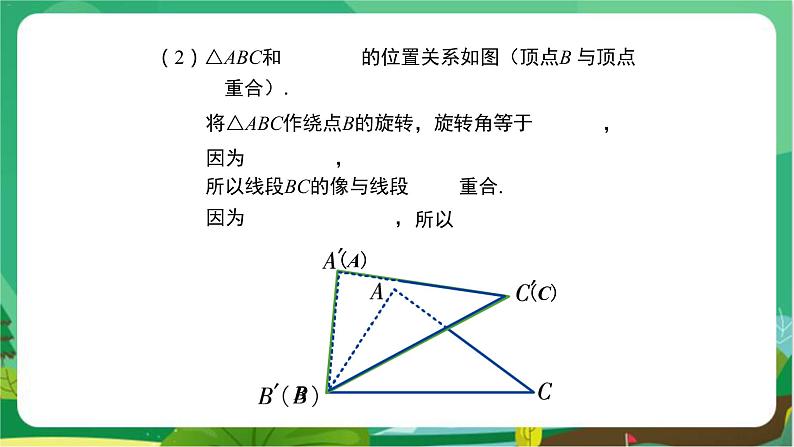
教学目标

1.掌握“边角边”定理的内容，能应用“边角边”判定两个三角形全等.

2.经历探索三角形全等的条件的过程，体会利用操作、归纳获得数学结论的方法.

3.培养学生观察分析图形的能力及运算能力，培养学生乐于探索的良好品质以及发现问题的能力.

教学重难点

重点：“边角边”定理.

难点：能运用“SAS”证明简单的三角形全等问题.

教学过程

导入新课

提出问题

（1）怎样的两个三角形是全等三角形？全等三角形的性质是什么？

（2）如果两个三角形有两条边和一个角分别对应相等，那么这两个三角形一定全等吗？此时应该有两种情况，一种是角夹在两条边的中间，形成两边一夹角，一种是角不夹在两边的中间，形成两边一对角，如图1所示.

图 1

探究新知

活动一：

在纸上的两个不同位置分别画一个三角形，它的一个角为50°，夹这个角的两边分别为2 cm，2.5 cm. 将这两个三角形叠在一起，它们完全重合吗？由此你能得到什么结论？

教师：你能发现什么？能猜想到什么结论？

学生：发现它们完全重合，可以猜测：两边和它们的夹角分别相等的两个三角形全等.

活动二：动手操作

如图2，设在△ABC和△A′B′C′中，∠ABC＝∠A′B′C′，AB＝A′B′，BC＝B′C′.

图 2

教师：将△ABC作平移，使BC的像B″C″与B′C′重合，△ABC在平移下的像为△A″B″C″.观察这两个三角形是否全等.为什么？

图 3

学生：全等，放在一起完全重合. 由于平移不改变图形的形状和大小，因此△ABC≌△A″B″C″.如图3.

活动三：动手实践操作

△ABC和△A′B′C′的位置关系如图4（顶点B与顶点B′重合）.

图 4

教师：这两个三角形全等吗？为什么？

根据前面的操作，鼓励学生用自己的语言来总结规律.

学生：全等，放在一起完全重合.

图 5

如图5，将△ABC作绕点B的旋转，旋转角等于∠C′BC，

因为BC＝B′C′，

所以线段BC的像与线段B′C′重合.

因为∠ABC＝∠A′B′C′，所以∠C′BC＝∠A′BA.

又因为BA＝B′A′，

所以在上述旋转下，BA的像与B′A′重合，

从而AC的像就与A′C′重合，

于是△ABC的像就是△A′B′C′.

由于旋转不改变图形的形状和大小，

因此△ABC≌△A′B′C′.

活动四：△ABC和△A′B′C′的位置关系如图6.

图 6

将△ABC作平移，使顶点B的像B″和顶点B′重合，两三角形全等吗？为什么？

学生：动手操作验证，尝试说明理由.

根据活动二、三的结论得

△A″B″C″≌△A′B′C′

因此△ABC≌△A′B′C′.

活动五：△ABC和△A′B′C′的位置关系如图7.

将△ABC作关于直线BC的轴反射，

图 7

学生：动手操作验证，尝试说明理由.

如图8，△ABC在轴反射下的像为△A′′BC.

由于轴反射不改变图形的形状和大小，

因此△ABC≌△A′′BC.

根据活动四的结论得△A″BC≌△A′B′C′，因此△ABC≌△A′B′C′.

图 8

教师：这两个三角形全等是因为满足哪三个条件？

学生：两边及其夹角分别相等.

根据前面的操作，鼓励学生用自己的语言来总结规律.

学生总结：判定两个三角形全等的基本事实：两边和及其夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）.

教师强调：角必须是已知两条边的夹角，边必须是已知角的两边.

几何语言：

如图9，在△ABC和△A′B′C′中，

∴ △ABC≌△A′B′C′（SAS）.

新知应用

例　如图10，AB和CD相交于O，且AO＝BO，CO＝DO.那么△ ACO和△BDO全等吗？

分析：如果要证明△ ACO ≌△ BDO，由题意可知，AO＝BO（已知），∠AOC＝∠BOD(对顶角)，CO＝DO (已知)，△ACO和△BDO具备“边角边”的条件.

证明：在△ACO和△BDO中，

∴ △ACO≌△BDO（SAS）.

归纳：证明三角形全等时，如果题目所给条件不充足，我们要充分挖掘图形中所隐藏的条件.如对顶角相等、公共角（边）相等等.

课堂练习

1.如图11，AB＝DB，BC＝BE，欲证△ABE≌△DBC，则需要增加的条件是(     )

A.∠A＝∠D                  B.∠E＝∠C

C.∠A＝∠C                  D.∠ABD＝∠EBC  

2.已知：如图12，AD∥BC，AD＝CB.

求证：△ADC ≌△CBA.        

图11　　　　　     　图12　　　　     　　　图13　

3.如图13，点A、E、B、D在同一条直线上，AE＝DB，AC＝DF，AC∥DF.请探索BC与EF有怎样的数量和位置关系？并说明理由.

4.如图14，去割一块与其形状，大小一样的玻璃，问带哪一块碎玻璃去可以使得新玻璃与原来的完全一样？

参考答案

1.D

2. 证明：∵ AD∥BC，

∴ ∠1＝∠2（两直线平行，内错角相等）.

在△ADC和△CBA中，

∴ △ADC≌△CBA（SAS）.

3. 解：∵ AC∥DF.

∴ ∠A＝∠D.（两直线平行，内错角相等）

又∵ AE＝DB，

∴ AE+BE＝DB+BE，即AB＝DE.

在△BCA和△EFD中，

∴ △BCA≌△EFD（SAS）.

∴ BC＝EF，（全等三角形的对应边相等）

∴ ∠ABC＝∠DEF，（全等三角形的对应角相等）

∴ EF∥BC.（内错角相等，两直线平行）

4.带碎玻璃Ⅲ去，可以根据SAS得到与原三角形玻璃全等的一块三角形玻璃.

课堂小结

1.三角形全等的判定：两边和它们的夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）.

2.求证两个三角形中的边或角相等时，一般要先证明这两个三角形全等.

注意：SAS中的角必须是两边的夹角，“A”必须在中间.

布置作业

教材第78页练习

板书设计

教学反思

教学反思

教学反思

教学反思

教学反思