第22练 简单几何体的表面积与体积-高考数学一轮复习小题多维练（新高考专用）

这是一份第22练 简单几何体的表面积与体积-高考数学一轮复习小题多维练（新高考专用），文件包含第22练简单几何体的表面积与体积-高考数学一轮复习小题多维练新高考专用解析版docx、第22练简单几何体的表面积与体积-高考数学一轮复习小题多维练新高考专用原卷版docx等2份试卷配套教学资源，其中试卷共22页， 欢迎下载使用。
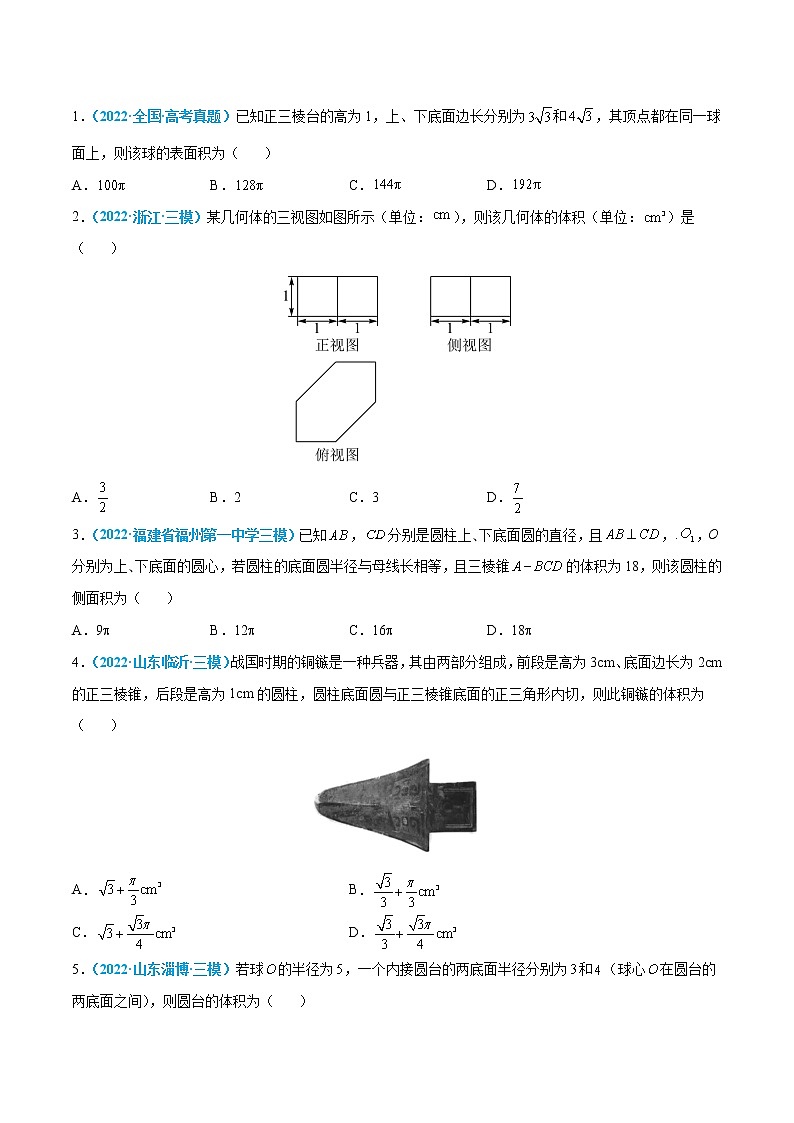
专题07  立体几何初步 第22练 简单几何体的表面积与体积1．（2022·天津·南开中学模拟）圆柱内有一个球，该球与圆柱的上、下底面及母线均相切，已知圆柱的体积为，则球的体积为（       ）A． B． C． D．【答案】A【解析】设球的半径为R，则圆柱的底面圆的半径为R，高为2R，所以，解得：，则球的体积为故选：A2．（2022·天津市新华中学模拟）已知圆柱的底面直径和高都等于球的直径，则球与圆柱体积比是（       ）A． B． C． D．【答案】A【解析】设球的半径为，则圆柱的底面半径为，高为，因为，所以．故选：A3．（2022·辽宁·二模）如图所示直三棱柱容器中，且，把容器装满水(容器厚度忽略不计)，将底面BCFE平放在桌面上，放水过程中当水面高度为AB的一半时，剩余水量与原来水量之比的比值为(       )A． B． C． D．【答案】A【解析】如图，柱体体积公式是底面积乘高，高没变，没有水的部分底面积变为原来的，故放出水量是原来水量的，剩余水量是原来水量的．故选：A．4．（2022·河北保定·一模）圆柱的底面直径与高都等于球的直径，则球的表面积与圆柱的侧面积的比值为（       ）A．1∶1 B．1∶2 C．2∶1 D．2∶3【答案】A【解析】设球的半径的r，依题意圆柱的底面半径也是r，高是2r，圆柱的侧面积= ，球的表面积为 ，其比例为1:1，故选：A.5．（2022·上海闵行·二模）已知一个圆柱的高不变，它的体积扩大为原来的4倍，则它的侧面积扩大为原来的___________倍.【答案】2【解析】设圆柱的高为，底面半径为，则体积为，体积扩大为原来的4倍，则扩大后的体积为，因为高不变，故体积，即底面半径扩大为原来的2倍，原来侧面积为，扩大后的圆柱侧面积为，故侧面积扩大为原来的2倍.故答案为：26．（2022·江苏江苏·一模）已知圆柱和圆锥的底面重合，且母线长相等，该圆柱和圆锥的表面积分别为，，则__________.【答案】【解析】设圆柱与圆锥的半径均为，母线为，故，，所以，故答案为：.1．（2022·全国·高考真题）已知正三棱台的高为1，上、下底面边长分别为和，其顶点都在同一球面上，则该球的表面积为（       ）A． B． C． D．【答案】A【解析】设正三棱台上下底面所在圆面的半径，所以，即，设球心到上下底面的距离分别为，球的半径为，所以，，故或，即或，解得符合题意，所以球的表面积为．故选：A．2．（2022·浙江·三模）某几何体的三视图如图所示（单位：），则该几何体的体积（单位：）是（       ）A． B．2 C．3 D．【答案】C【解析】从三视图可以得到直观图为直六棱柱，如图所示，在俯视图中，可以求出底面积为，从正视图和侧视图可知直六棱柱的高为1，所以该几何体的体积是.故选：C.3．（2022·福建省福州第一中学三模）已知，分别是圆柱上､下底面圆的直径，且，.，O分别为上､下底面的圆心，若圆柱的底面圆半径与母线长相等，且三棱锥的体积为18，则该圆柱的侧面积为（       ）A．9 B．12 C．16 D．18【答案】D【解析】分别过作圆柱的母线，连接，设圆柱的底面半径为则三棱锥的体积为两个全等四棱锥减去两个全等三棱锥即，则圆柱的侧面积为故选：D．4．（2022·山东临沂·三模）战国时期的铜镞是一种兵器，其由两部分组成，前段是高为3cm、底面边长为2cm的正三棱锥，后段是高为1cm的圆柱，圆柱底面圆与正三棱锥底面的正三角形内切，则此铜镞的体积为（       ）A． B．C． D．【答案】A【解析】由题意，铜镞的直观图如图所示，三棱锥的体积，因为圆柱的底面圆与正三棱锥底面的正三角形内切，所以圆柱的底面圆的半径，所以圆柱的体积所以此铜镞的体积为故选：A.5．（2022·山东淄博·三模）若球的半径为，一个内接圆台的两底面半径分别为和（球心在圆台的两底面之间），则圆台的体积为（       ）A． B．C． D．【答案】A【解析】解：如图，由题意可知，，，，则，，圆台的高为，圆台体积为．故选：A．6．（2022·湖北·黄冈中学三模）圆柱上、下底面的圆周都在一个体积为的球面上，圆柱底面直径为8，则该圆柱的体积为_______【答案】【解析】球的半径为，，解得，圆柱的高为：．可得．故答案为：．7．（2022·湖南岳阳·模拟）某球形巧克力设计了一种圆柱形包装盒，每盒可装7个球形巧克力，每盒只装一层，相邻的球形巧克力相切，与包装盒接触的6个球形巧克力与包装盒相切，如图是平行于底面且过圆柱母线中点的截面，设包装盒的底面半径为，球形巧克力的半径为，每个球形巧克力的体积为，包装盒的体积为，则 ________【答案】【解析】由图知，包装盒的高为，因此，，又，所以.故答案为：8．（2022·湖北·模拟）表面积为的多面体的每一个面都与体积为的球相切，则这个多面体的体积为__________.【答案】【解析】解：因为球的体积为．设球的半径为，所以，解．因为表面积为的多面体的每一个面都与体积为的球相切，所以球的半径就是球心到多面体面的距离，所以多面体的体积为．故答案为：．9．（2022·山西吕梁·三模（文））已知球的一个截面面积为，若球上的点到该截面的最大距离为3，则球的表面积为__________．【答案】【解析】设球的半径为，截面圆的半径为到截面的距离为，则由题意得 解得所以球的表面积为故答案为：10．（2022·天津红桥·二模）两个圆锥的底面是一个球的同一个截面，顶点均在球面上，若球的体积为，两个圆锥的高之比为1:3，则这两个圆锥的体积之和为______.【答案】【解析】设球的半径为，因为球的体积为，所以有，设两个圆锥的高分别为，于是有且，所以有，设圆锥的底面半径为，所以有，因此这两个圆锥的体积之和为，故答案为：1．（2022·北京二中模拟）如图所示，一套组合玩具需在一半径为3的球外罩上一个倒置圆锥，则圆锥体积的最小值为（       ）A．64π B．40π C．84π D．72π【答案】D【解析】解：设母线与底面的夹角，底面半径，内切球半径，圆锥的高，则：，，圆锥的体积，而，，所以， 又因为：定值所以，当且仅当，即时，所以．故选：D．2．（2022·福建·三明一中模拟）已知一个圆柱的底面直径与高都等于球O的半径，则该圆柱的表面积与球O的表面积之比为（       ）A． B． C． D．【答案】C【解析】设球的半径为,则该圆柱的底面半径为，高为所以圆柱的表面积为：,球的表面积为：则圆柱的表面积与球的表面积之比为故选：C3．（2022·山东泰安·模拟）在底面是正方形的四棱锥中，底面ABCD，且，则四棱锥内切球的表面积为（       ）A． B． C． D．【答案】B【解析】解：由题意，设四棱锥内切球的半径为r，因为，四棱锥的表面积，所以，所以四棱锥内切球的表面积为.故选：B.4．（2022·山东聊城·三模）《几何原本》是古希腊数学家欧几里得的一部不朽之作，其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.若一个直角圆锥的侧面积为，圆锥的底面圆周和顶点都在同一球面上，则该球的体积为（       ）A． B． C． D．【答案】B【解析】设球半径为，圆锥的底面半径为，若一个直角圆锥的侧面积为，设母线为，则，所以直角圆锥的侧面积为：，可得：，，圆锥的高，由，解得：，所以球的体积等于，故选：B5．（2022·广东·华南师大附中三模）已知圆锥的顶点为P，母线长为2，底面圆直径为，A，B，C为底面圆周上的三个不同的动点，M为母线PC上一点，则下列说法正确的是（       ）A．当A，B为底面圆直径的两个端点时，B．△PAB面积的最大值为C．当△PAB面积最大值时，三棱锥C-PAB的体积最大值为D．当AB为直径且C为弧AB的中点时，的最小值为【答案】ACD【解析】对于A，记圆锥底面圆心为O，，所以，所以，故A正确；对于B，设，则截面三角形的面积，故B不正确；对于C，由选项B中推理可知，此时，所以点C到AB的距离的最大值为，从而可知三棱锥C-PAB的体积最大值为，故C选项正确；对于D，由题意可得△PAC和△PBC全等，在△PAC中，，，所以，进而，记PC边上的高为h（垂足为Q），则，所以，当M与Q重合时取等号，故D选项正确；故选：ACD．6．（2022·湖南师大附中三模）如图，水平桌面上放置一个棱长为4的正方体水槽，水面高度为2，水槽侧面上有一个小孔E，点E到直线CD的距离为3，将该水槽绕CD倾斜（CD始终在桌面上）至恰有水从小孔流出，则在倾斜过程中，下列说法正确的有（     ）A．没水的部分始终呈四棱柱形B．水面始终经过水槽的外接球的球心C．水面的面积为定值D．E到桌面的最小距离为【答案】AB【解析】设水面与棱交于点，与棱交于点，与棱交于点，与棱交于点，由四棱柱的定义，几何体为直四棱柱，故A正确；水槽绕CD倾斜至恰有水从小孔流出过程中，水的体积不变，，所以线段分别恒过正方形的中心，即水面恒过正方体体心，又因为正方体体心为其外接球球心，B显然正确；对于C选项：水面的面积，由于不为定值，所以水面面积不为定值，故C错误；对于D选项；易知水槽绕CD倾斜至恰有水从小孔流出时E到桌面的距离最小，如图，桌面，到桌面的距离等于到桌面的距离，，故D错误.故选：AB.7．（2022·广东广州·三模）某班级到一工厂参加社会实践劳动，加工出如图所示的圆台，在轴截面中，，且，则（       ）A．该圆台的高为B．该圆台轴截面面积为C．该圆台的体积为D．一只小虫从点沿着该圆台的侧面爬行到的中点，所经过的最短路程为【答案】BCD【解析】如图，作交于，易得，则，则圆台的高为，A错误；圆台的轴截面面积为，B正确；圆台的体积为，C正确；将圆台一半侧面展开，如下图中，设为中点，圆台对应的圆锥一半侧面展开为扇形，由可得，则，，又，则，即点到的中点所经过的最短路程为，D正确.故选：BCD.8．（2022·辽宁·抚顺市第二中学三模）已知空间四边形，，，，，球心O在平面ABC上，且与直线PA、直线PB、直线PC都相切，则球O的半径为__________．（直线与球面有唯一公共点称为直线与球相切）【答案】【解析】过点作平面,垂足为，∴△≌△≌△,∴,∴为△外接圆的圆心， 又∵△为正三角形，∴为△外接圆的中心，由对称性可知点和重合，由已知得,过点作边上的垂线,垂足为，即,,   ,设与球心O相切于点，则,,则球O的半径为,故答案为：.9．（2022·河北·模拟）如图，在正三棱柱中，与平面所成的角为，则该三棱柱外接球的表面积为___________.【答案】【解析】如图，取BC的中点M，连结A1M，AM，因为是正三棱柱，所以球心O在上下底面中心O1O2连线的中点，即外接球的半径R=OA1，又因为与平面所成的角为，所以AA1与平面所成的角为，又因为是正三棱柱，所以∠AA1M=45°，所以，所以所以外接球面积为.故答案为：.10．（2022·福建省福州第一中学三模）在三棱锥中，平面，，，则三棱锥外接球的表面积为___________；若动点M在该三棱锥外接球上，且，则点M的轨迹长为___________.【答案】          【解析】由平面，得，三棱锥为直三棱锥，其外接球相当于以为棱的长方体的外接球，故外接球半径为，故三棱锥外接球的表面积为；如图，中点为F，则易得以为棱的正方体，由正方体的对称性，要使，则M在的角平分面上，即面，故M的轨迹为面与外接球相交出的圆.取AP、HE中点I、J，由正方体的对称性易得面面，且，故，故IJ上的高，故M的轨迹圆的半径，故轨迹长为.故答案为：；