




人教版九年级上册24.2.1 点和圆的位置关系优秀ppt课件
展开24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
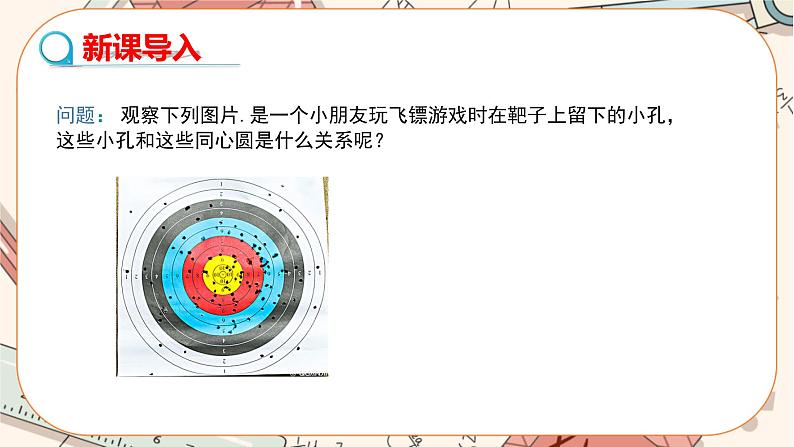
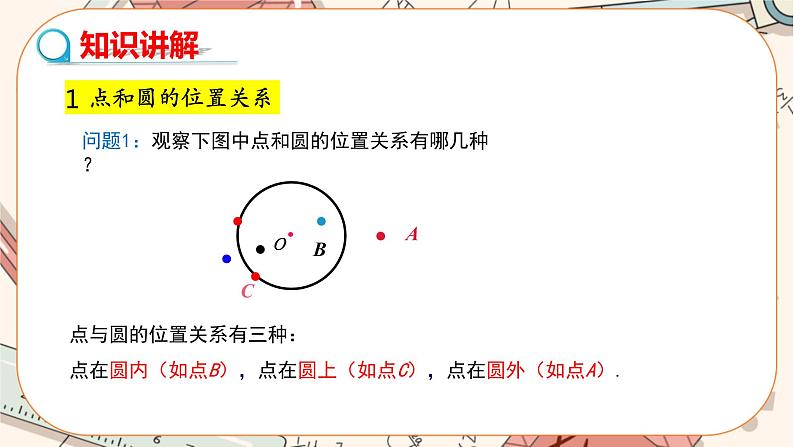
教学目标 1.了解点和圆的三种位置关系,掌握点到圆心的距离与半径之间的关系. 2.掌握“不在同一条直线上的三点确定一个圆”,并能作出这个圆. 3.了解反证法的意义,会用反证法进行简单的证明. 教学重难点 重点:1.理解并掌握点和圆的三种位置关系;2.理解不在同一条直线上的三个点确定一个圆及其运用. 难点:1.理解三角形的外接圆和三角形外心的概念;2.了解反证法的证明思路,会进行三角形中位线的性质定理的证明. 教学过程 导入新课 问题: 观察下列图片.是一个小朋友玩飞镖游戏时在靶子上留下的小孔,这些小孔和这些同心圆是什么关系呢? 探究新知 1.点和圆的位置关系 【问题情境】观察下图中点和圆的位置关系有哪几种?
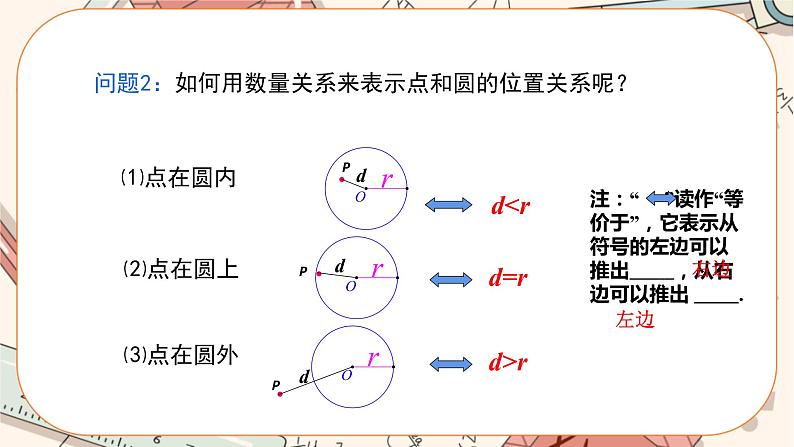
师生活动:小组合作交流,小组代表发言,教师适当点拨. 【归纳总结】 点与圆的位置关系有三种:点在圆内(如点B),点在圆上(如点C),点在圆外(如点A). 【问题情境】如何用数量关系来表示点和圆的位置关系呢? 师生活动:学生思考,教师巡视,适时指导. 【归纳总结】设⊙O的半径为r,点P到圆心的距离OP=d,则有: (1)点P在圆外⇔ ; (2)点P在圆上⇔ ;(3)点P在圆内⇔ .
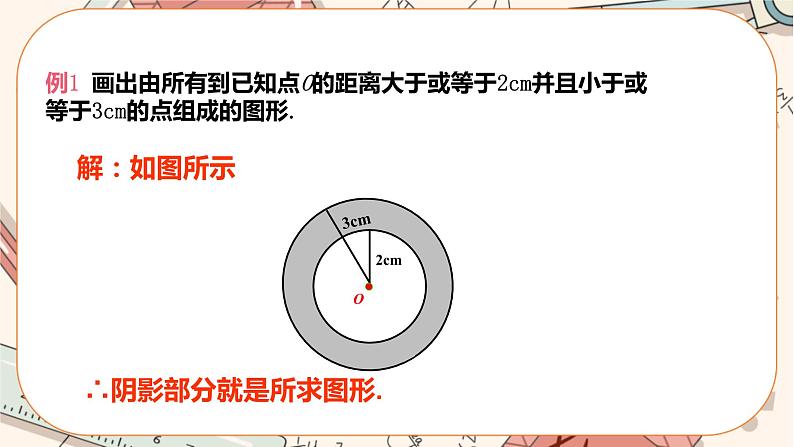
注:“⇔”读作“等价于”,它表示从符号的左边可以推出右边,从右边可以推出左边 . 【新知应用】 例1 画出由所有到已知点O的距离大于或等于2 cm并且小于或等于3 cm的点组成的图形. 师生活动:学生动手画图,教师巡视,个别指导. 【解】如图所示,阴影部分就是所求图形.
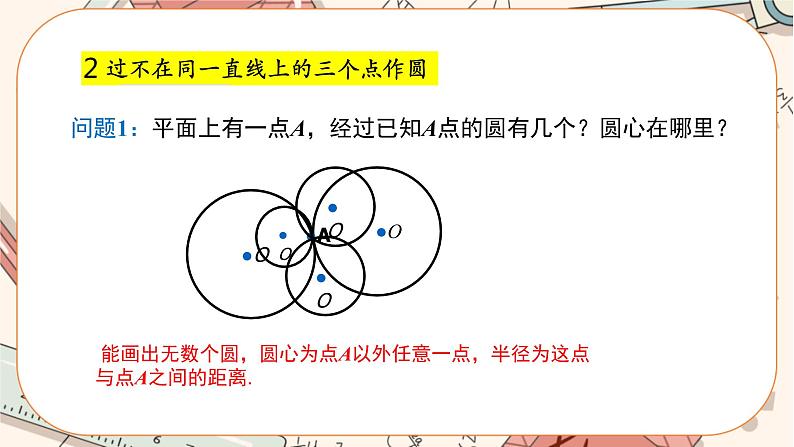
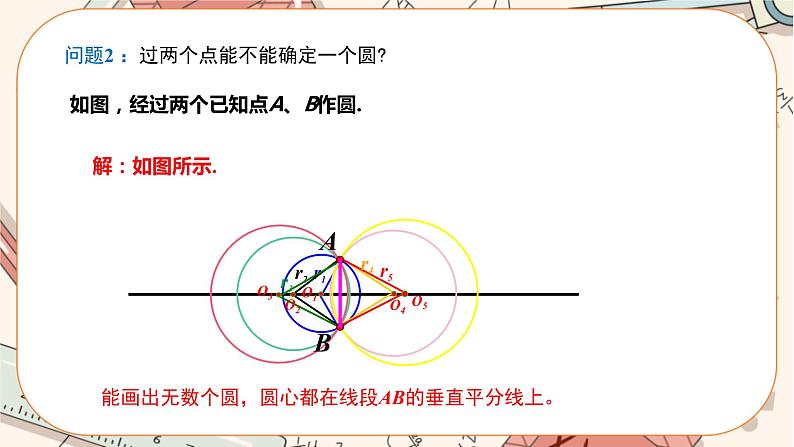
2.过不在同一条直线上的三个点作一个圆 【问题情境1】平面上有一点A,经过已知A点的圆有几个?圆心在哪里? 师生活动:学生动手操作,教师点拨. 【解】 【归纳总结】能画出无数个圆,圆心为点A以外任意一点,半径为圆心与点A之间的距离. 【问题情境2】:过两个点能不能确定一个圆? 师生活动:学生动手操作,讨论交流,教师适时指导. 【解】
【归纳总结】能画出无数个圆,圆心都在线段AB的垂直平分线上. 【问题情境3】:经过不在同一条直线上的三点A,B,C能不能作圆?如果能,如何确定所作的圆心? 师生活动:教师适时引导分析,学生在教师的引导下,思考动手画图,再抽一名学生口述作图过程,教师再在黑板上板书尺规作图细节. 作法: (1)连接AB,BC; (2)分别作AB,BC的垂直平分线,交于O.点O就是所求圆的圆心. 【归纳总结】不在同一直线上的三个点确定一个圆. 3.三角形的外接圆与外心 (1)经过三角形(△ABC)的三个顶点可以作一个圆,这个圆叫做三角形的外接圆. (2)外接圆的圆心是三角形三条边的 的交点,叫做这个三角形的 . 例2 分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
师生活动:学生动手画图,仔细观察图形,发现规律,教师适时点拨. 【归纳总结】 (1)锐角三角形的外心位于三角形内. (2)直角三角形的外心位于直角三角形斜边的中点处. (3)钝角三角形的外心位于三角形外. 4.反证法 【问题情境】经过同一条直线上的三点能作出一个圆吗? 师生活动:学生动手作图,发现怎么也画不出这样的圆,得出结论:过同一条直线上的三点不能作圆,教师点拨,介绍反证法. 反证法:不是直接从命题的已知得出结论,而是假设命题的结论不成立,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立.这种证明方法叫做反证法. 例3 用反证法的证明:经过同一条直线上的三个点不能作出一个圆. 证明:如图,假设过同一条直线l上的A,B,C三点可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点,而l1⊥l,l2⊥l,这与我们以前所学的“过一点有且只有一条直线与已知直线垂直”矛盾.所以,过同一条直线上的三个点不能作圆. 【归纳总结】 反证法的一般步骤:①假设命题的结论不成立; ②从这个假设出发,经过推理,得出矛盾; ③由矛盾判定假设不正确,从而肯定命题的结论正确. 【新知应用】 例4 如图,⊙O的半径r=10,圆心O到直线l的距离OD=6,在直线l上有A,B,C三点,AD=6,BD=8,CD=5,问A,B,C三点与⊙O的位置关系如何? 师生活动:(引发学生思考)判断点与圆的位置关系的关键是判断点到圆心的距离与半径大小之间的大小关系. 【解】∵OA==6<10,∴点A在⊙O内. ∵OB==10,∴点B在⊙O上. ∵OC==>10,∴点C在⊙O外. 【归纳总结】(学生总结,老师点评)判断点与圆的位置关系的关键是比较点到圆心的距离与半径的大小.同时注意垂径定理和勾股定理的应用. 【拓展延伸】 例5 如图,在Rt△ABC中,∠ACB=90°,AC=6,CB=8,AD是△ABC的角平分线,过A,D,C三点的圆与斜边AB交于点E,连接DE. (1)求证:AC=AE; (2)求△ACD外接圆的直径. 师生活动:(引发学生思考)证明线段相等的方法有哪些?结合图形,适合用哪种方法?看到∠ACB=90°,结合图形能得到哪些结论?对于求直径又该使用哪种方法? 【解】(1)证明:∵∠ACB=90°,且∠ACB为⊙O的圆周角,∴AD为⊙O的直径, ∴∠AED=90°,∴∠ACB=∠AED. ∵AD是△ABC中∠BAC的平分线,∴∠CAD=∠EAD,∴CD=DE, 在Rt△ACD与Rt△AED中, ∴△ACD≌△AED(HL),∴AC=AE. (2)∵AC=6,BC=8,∴AB==10. 由(1)得,∠AED=∠BED=90°. 设CD=DE=x,则DB=BC-CD=8-x,EB=AB-AE=10-6=4. 在Rt△BED中,根据勾股定理,得BD2=BE2+ED2,即(8-x)2=x2+42,解得x=3,∴CD=3. ∵AC=6,∴AD2=AC2+CD2=62+32=45,∴AD=3. 【归纳总结】(学生总结,老师点评)全等三角形的对应边相等是常用的证明线段相等的一种方法;利用三角形的外接圆的性质和勾股定理,直角三角形的外接圆直径大小就是直角三角形的斜边长. 课堂小结 学生独立总结,教师补充. 1.点和圆的位置关系; 2.过不在同一条直线上的三个点确定一个圆; 3.三角形的外接圆和外心; 4.反证法. 布置作业 教材101页第7题和102页第8、9题. 板书设计 24.2.1 点和圆的位置关系 1.点与圆的三种位置关系与对应的数量关系: 设⊙O的半径为r,点P到圆心的距离OP=d,则有: ①点P在圆内d<r;②点P在圆上d=r;③点P在圆外d>r. 2.不在同一条直线上的三个点确定一个圆. 3.三角形的外接圆与外心. 4.反证法. |
初中数学人教版九年级上册24.2.1 点和圆的位置关系图片ppt课件: 这是一份初中数学人教版九年级上册24.2.1 点和圆的位置关系图片ppt课件,共24页。PPT课件主要包含了点和圆的位置关系,点在圆内,d﹤r,点在圆上,点在圆外,d=r,练一练,﹤r﹤5,不能作出,为什么等内容,欢迎下载使用。
数学九年级上册24.2.1 点和圆的位置关系教学课件ppt: 这是一份数学九年级上册24.2.1 点和圆的位置关系教学课件ppt,共23页。PPT课件主要包含了学习目标,情景引入,知识精讲,针对练习,数形结合,位置关系,数量关系,典例解析,达标检测,小结梳理等内容,欢迎下载使用。
初中数学人教版九年级上册24.2.1 点和圆的位置关系教课课件ppt: 这是一份初中数学人教版九年级上册24.2.1 点和圆的位置关系教课课件ppt,共25页。PPT课件主要包含了课堂练习等内容,欢迎下载使用。













