初中数学13.3 全等三角形的判定教学课件ppt

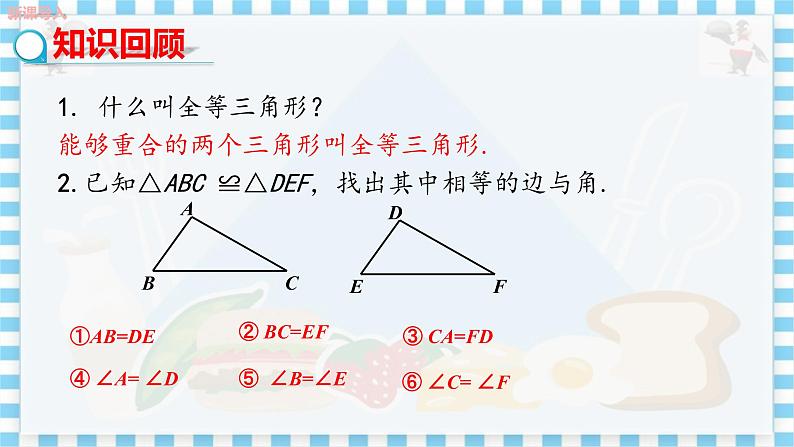
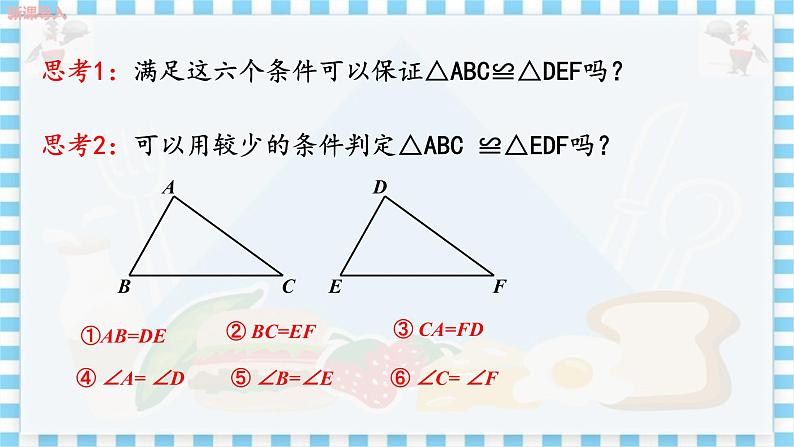
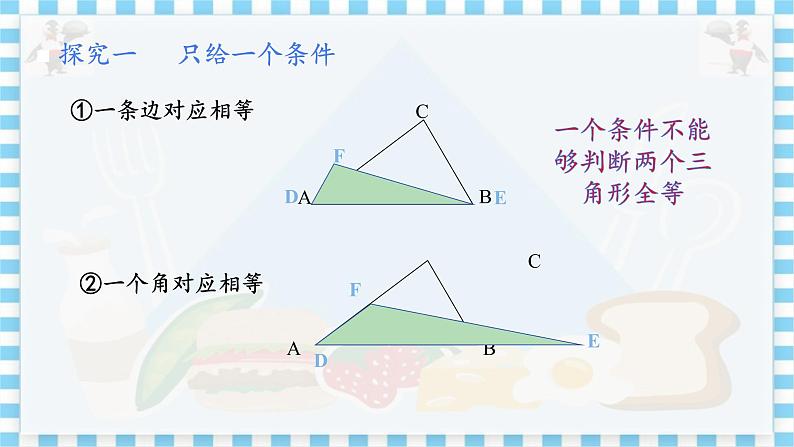
教学目标

1.进行三角形全等条件的探索，积累数学活动经验；

2.掌握基本事实一，利用基本事实一证明两个三角形全等；

3.会利用三角形全等证明线段相等、角相等.

教学重难点

重点：掌握基本事实一，利用基本事实一证明两个三角形全等；

难点：会利用三角形全等证明线段相等、角相等.

教学过程

导入新课

1.什么叫全等三角形？能够完全重合的两个三角形叫全等三角形.

2.如图，已知△ABC ≌△DEF，找出其中相等的边与角.

①AB＝DE，② BC＝EF，③CA＝FD；

④∠A＝∠D， ⑤∠B＝∠E，⑥∠C＝∠F.

探究新知

一、探究互动一

思考1：满足上述六个条件可以保证△ABC≌△DEF吗？

思考2：可以用较少的条件判定△ABC ≌△DEF吗？

在以上六个条件中，能否选择其中部分条件，简捷地判定两个三角形全等呢？

教师引导，学生探究（小组合作）

探究1  只给一个条件，可以分哪几种情况？能够判断两个三角形全等吗？

①一条边对应相等：如右图，保证了一条边重合，但

两个三角形不全等；

②一个角对应相等：如右图，保证了一个角重合，但

两个三角形不全等；

结论：一个条件不能够判断两个三角形全等.

探究2   只给两个条件.

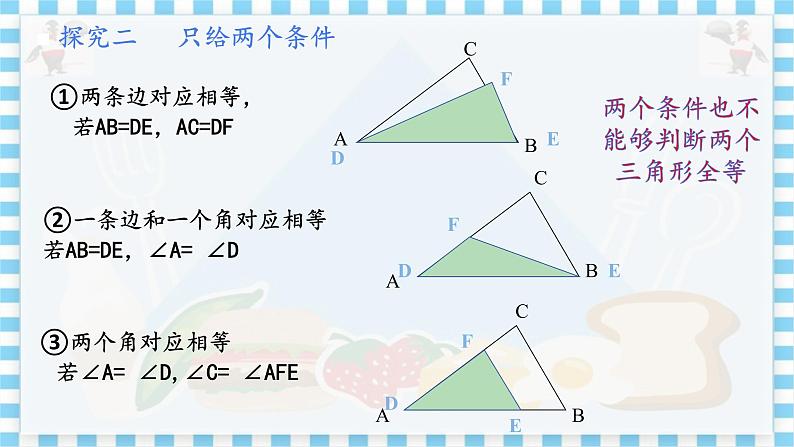
①两条边对应相等：

若AB＝DE，AC＝DF,但两个三角形不全等；

②一条边和一个角对应相等：

若AB＝DE，∠A＝ ∠D，但两个三角形不全等；

③两个角对应相等：

  若∠A＝ ∠D,∠C＝ ∠AFE，但两个三角形不全等.

结论：两个条件也不能够判断两个三角形全等.

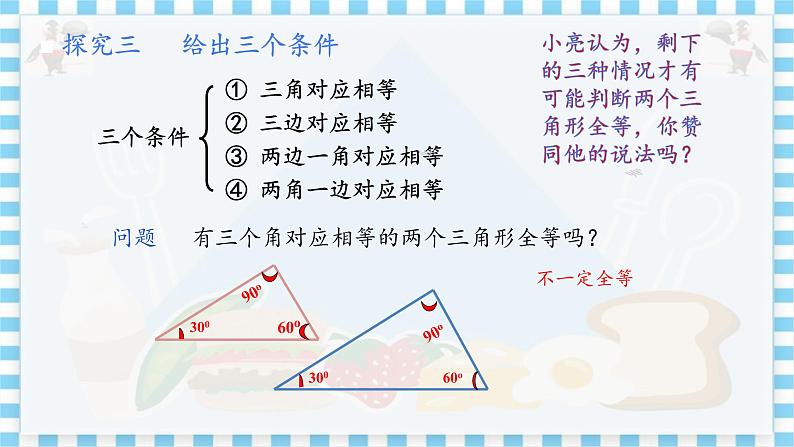
探究3   给出三个条件.

　　问题   有三个角对应相等的两个三角形全等吗？

结论：不一定全等.

小亮认为，剩下的三种情况才有可能判断两个三角形全等，你赞同他的说法吗？

二、探究互动二——基本事实一

问题1：准备一些长都是13 cm的细铁丝.和同学一起，每人用一根铁丝，折成一个边长分别是3 cm，4 cm，6 cm的三角形. 把你做出的三角形和同学做出的三角形进行比较，它们能重合吗?

问题2：准备一些长都是13 cm的细铁丝.和同学一起，每人用一根铁丝，余下 1 cm，用其余部分折成边长分别是3 cm，4 cm，5 cm的三角形. 再和同学做出的三角形进行比较，它们能重合吗?

小组互动，教师指导.

归纳：

基本事实一：如果两个三角形的三边对应相等，那么这两个三角形全等（可简记为“_______”或“_____”）.

几何语言：如图，在△ABC和△ DEF中，

∴ △ABC ≌△ DEF（      ）.

例1　如图1，已知点A，D，B，F在一条直线上，AC＝FE，BC＝DE，AD＝FB.

求证：△ABC≌△FDE.

教师指导，学生分析：

在两个三角形中分别找到对应的三条边，然后证明它们分别相等.

证明：∵ AD＝FB，∴ AD+DB＝FB+DB，即AB＝FD.

在△ABC和△FDE中，∵

∴ △ABC≌△FDE(SSS).

图1                  图2

例2　如图2，已知：AB＝AC，AD＝AE，BD＝CE.

求证：∠BAC＝∠DAE.

证明：在△ABD和△ACE中，

∵

∴ △ABD≌△ACE(SSS)，∴ ∠BAD＝∠CAE.

∴ ∠BAD＋∠DAC＝∠CAE＋∠DAC，

即∠BAC＝∠DAE.

练习：1.如图，下列三角形中，与△ABC全等的是_______.

2.已知：如图，AB＝DE，AC＝DF，BF＝CE．

求证:(1)∠A＝∠D;(2)AB∥DE.

学生独立完成，教师评价

1.③

2.证明：（1） ∵ BF＝CE，

        ∴ BF+FC＝FC+CE，即BC＝EF.

在△ABC和△DEF中，

      ∵

∴ △ABC≌△DEF(SSS)，

  ∴ ∠A＝∠D.

（2）由（1）△ABC≌△DEF，可得∠B＝∠E，∴ AB∥DE.

三、三角形的稳定性

问题1：猜想三角形和四边形哪一种结构更加牢靠？

问题2：观察右面两组木架，如果分别扭动它们，会得到怎样的结果？

教师归纳：

三角形的特性：

三角形木架的形状_________，也就是说三角形是具有_____的图形.

四边形的特性：

四边形木架的形状_______，也就是说四边形是_________的图形.

理解“稳定性”

只要三角形三条边的长度固定，这个三角形的形状和大小也就完全确定，三角形的这种性质叫做“三角形的稳定性”.

这就是说，三角形的稳定性不是“拉得动、拉不动”的问题，其实质应是“三角形边长确定，其形状和大小就确定了”.

想一想：在我们日常生活中，还有哪些地方运用到了三角形的稳定性？你能举出例子来吗？

课堂练习

1.如图1，在△ABC中，AB＝AC，BE＝CE，则由“SSS”可以判定(       )

A.△ABD≌△ACD B.△BDE≌△CDE C.△ABE≌△ACE  D.以上都不对

2.下列关于三角形稳定性和四边形不稳定性的说法中正确的是(       )

A.稳定性总是有益的，而不稳定性总是有害的

B.稳定性有利用价值，而不稳定性没有利用价值

C.稳定性和不稳定性均有利用价值

D.以上说法都不对

3.在生活中我们常常会看见如图2所示的情况加固电线杆，这是利用了三角形的________.

4.如图3，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有(       )

A. 1个  B. 2个   C. 3个   D. 4个

5.如图4，D，F是线段BC上的两点，AB＝CE，AF＝DE，要使△ABF≌△ECD，还需要条件 ________   (填一个条件即可）.

6.如图5，AD＝BC，AC＝BD.求证：∠C＝∠D .

图1 　　           图2  　　　            图3             

图4　　　　　　　　　图5

参考答案

1.C     2.C   3.稳定性    4.C     5.BD＝CF(答案不唯一)

6.证明：连接AB（图略）,在△ABD和△BAC中，

∴ △ABD≌△BAC(SSS)，∴ ∠D＝∠C.

课堂小结

1.基本事实一；

2.基本事实一的应用；

3.三角形的稳定性.

布置作业

完成教材第40页习题.

板书设计 

 13.3　全等三角形的判定

第1课时 边边边

教学反思

教学反思

教学反思

教学反思

教学反思