








初中数学冀教版八年级上册17.3 勾股定理教学ppt课件
展开第十七章 特殊三角形
17.3 勾股定理
第2课时 勾股定理的实际应用
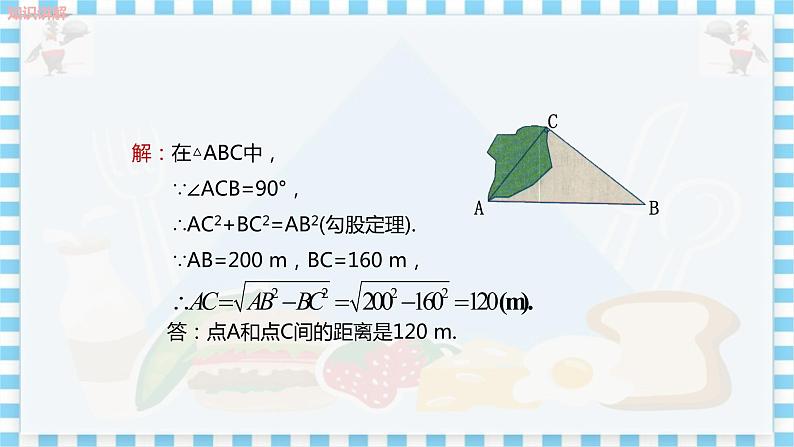
教学目标 1.会运用勾股定理解决简单的实际问题. 2.能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长度之间的联系,并进一步求出未知边长. 教学重难点 重点:运用勾股定理解决简单的实际问题. 难点:能从实际问题中抽象出直角三角形模型,利用勾股定理解决问题. 教学过程 旧知回顾 1.回顾勾股定理: 如果直角三角形两直角边分别为a,b,斜边为c,那么. 2.回顾使用勾股定理的注意事项: (1)在直角三角形中; (2)看清哪个是直角; (3)已知两边,没有指明是直角边还是斜边时,一定要分类讨论. 导入新课 生活故事引入“勾股定理的实际应用”:——竹竿进门 同一根长竹竿以三种不同的方式(平行于上门框、平行于左门框、沿门的对角线)进门,结合这三种情况,对于长竹竿进门之类的问题你有什么想法? 学生回答:主要看门框的对角线长,如果竹竿的长小于门框对角线的长,则竹竿能进门;否则不能进门. 师问:求门框对角线的长用到什么知识? 生答:勾股定理. 勾股定理能解决直角三角形的许多问题,因此在现实生活中有着广泛的应用.本节课我们就来学习勾股定理的应用. 探究新知 勾股定理的实际应用 例1 如图,为了测得湖边上点A和点C间的距离,一观测者在点B设立了一根标杆,使∠ACB=90°.测得AB=200m,BC=160m.根据测量结果,求点A和点C间的距离. (1)阅读例题,分析题目中的已知条件和未知条件. (2)怎样求出AC的长度?要用我们学过的哪方面的知识? 本题已知直角三角形的一直角边和斜边,求另一直角边,可以利用勾股定理解决. (3)请同学们在练习本上完成,指一名学生板演,教师指导步骤. (4)对学生的解题过程进行讲评. 解:在△ABC中, ∵ ∠ACB=90°, ∴ AC2+BC2=AB2(勾股定理). ∵ AB=200 m,BC=160 m, ∴ AC==120(m). 答:点A和点C间的距离是120 m. 点睛:基本思想方法:勾股定理把“形”与“数”有机地结合起来,即把直角三角形这个“形”与三边关系这一“数”结合起来,它是数形结合思想的典范. 练一练:如图是某厂房屋顶的三角架的示意图.已知AB=AC=17 m,AD⊥BC,垂足为D,AD=8 m,求BC的长.
学生独立完成,指一名学生板演. 解:在Rt△ABD中, ∵AB=17 m,AD=8 m, ∴BD2=AB2-AD2=172-82=225, ∴BD=15 m, ∵AB=AC,AD⊥BC, ∴BC=2BD=30 m. 例2 如图所示,在长为50 mm,宽为40 mm的长方形零件上有两个圆孔,与孔中心A,B相关的数据如图所示.求孔中心A和B间的距离. 教师引导学生分析题意,提问: (1)在直角三角形中怎样求斜边的长度? (2)AC,BC的长度怎样求? (3)在练习本上写出求解过程. 学生独立思考交流,得出:要求斜边AB的长度,就要求出两直角边AC和BC的长度,这样就可以根据勾股定理的变形AB=求出AB的长度. 利用线段的平移可求出AC=50-15-26=9(mm),BC=40-18-10=12(mm). 解:∵△ABC是直角三角形, ∴AB2=AC2+BC2. ∵AC=50-15-26=9(mm), BC=40-18-10=12(mm), ∴AB==15(mm). 答:孔中心A和B间的距离是15 mm. 例3 在水平如镜的湖面上,有一朵美丽的红莲,它高出水面3尺,一阵大风吹过,红莲被吹至一边,花朵齐及水面,如果知道红莲移动的水平距离为6尺,问湖水多深? 解:如图,设红莲在无风时高出水面部分CD长为3尺,点B为红莲被吹斜后花朵的位置,BC部分长6尺.设水深AC为x尺, 在Rt△ABC中,AC2+BC2=AB2(勾股定理). 又∵AB=AD=(x+3)尺, ∴(x+3)2=x2+62,解得x=4.5. 答:湖水深4.5尺. 通过上面几个例题的分析,师生共同归纳: 勾股定理的实际应用的一般步骤: (1)读懂题意,分析已知、未知间的关系; (2)构造直角三角形; (3)利用勾股定理等列方程; (4)解决实际问题.
课堂练习
A.25海里 B.30海里 C.40海里 D.50海里
图1 图2 图3 2.如图2,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙脚的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( ) A.0.7米 B.1.5米 C.2.2米 D.2.4米 3.如图3是一张直角三角形的纸片,两直角边AC=6 cm,BC=8 cm,将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( ) A.4 cm B.5 cm C.6 cm D.10 cm 4.如图所示的是在机器人创意大赛中,一参赛队员设计的机器人比赛时行走的路径,机器人从A点先往东走4 m,又往北走1.5 m,遇到障碍后又往西走2 m,再转向北走4.5 m处,往东一拐,仅走0.5 m就到达了B点.A,B两点间的距离是多少? 参考答案 1.C 2.C 3.B 4.解:如图所示,过点B作BC⊥AD于C, 由题知AC=4-2+0.5=2.5(m), BC=4.5+1.5=6(m),在直角三角形ABC中,AB为斜边,
课堂小结 1.勾股定理的实际应用的一般步骤: (1)读懂题意,分析已知、未知间的关系; (2)构造直角三角形; (3)利用勾股定理等列方程; (4)解决实际问题. 2.数学思想 基本思想方法:勾股定理把“形”与“数”有机地结合起来,即把直角三角形这个“形”与三边关系这一“数”结合起来,它是数形结合思想的典范. 布置作业 完成教材习题154页A组 . 板书设计 17.3 勾股定理 第2课时 勾股定理的实际应用
| 教学反思
教学反思
教学反思
教学反思
|
数学八年级上册17.3 勾股定理教学ppt课件: 这是一份数学八年级上册17.3 勾股定理教学ppt课件,文件包含教学课件八上·冀教·173勾股定理第3课时勾股定理的逆定理pptx、1733docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
初中数学17.3 勾股定理教学ppt课件: 这是一份初中数学17.3 勾股定理教学ppt课件,文件包含教学课件八上·冀教·173勾股定理第1课时勾股定理pptx、1731docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
初中数学冀教版八年级上册17.3 勾股定理示范课ppt课件: 这是一份初中数学冀教版八年级上册17.3 勾股定理示范课ppt课件,共18页。PPT课件主要包含了议一议,SA+SBSC,a2+b2c2等内容,欢迎下载使用。













