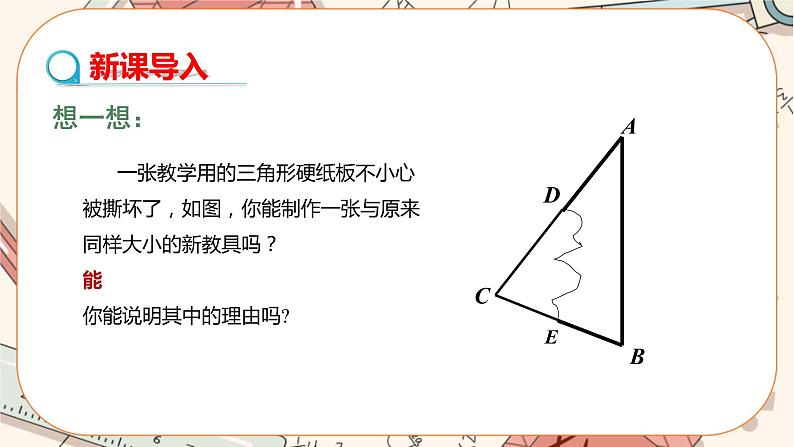
人教版八年级上册12.1 全等三角形优秀ppt课件

12.2　三角形全等的判定

第3课时

学习目标

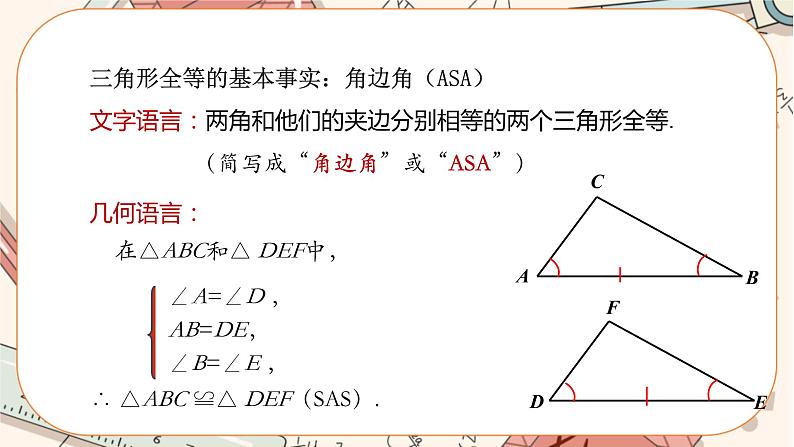
1.掌握“角边角”“角角边”定理的内容，能初步应用“角边角”“角角边”定理判定两个三角形全等.

2.经历探究三角形全等条件的活动，体验用操作、归纳的方法得出数学结论的过程，培养发现问题、解决问题的能力.

3.通过探究三角形全等条件的活动，培养敢于面对困难、克服困难的信心.

自主学习

学习任务一　回顾知识

1.三角形中已知三个元素，有哪几种情况？

2.到目前为止，可以作为判定两个三角形全等的方法有几种？各是什么？

3.AAA能判断两个三角形全等吗？

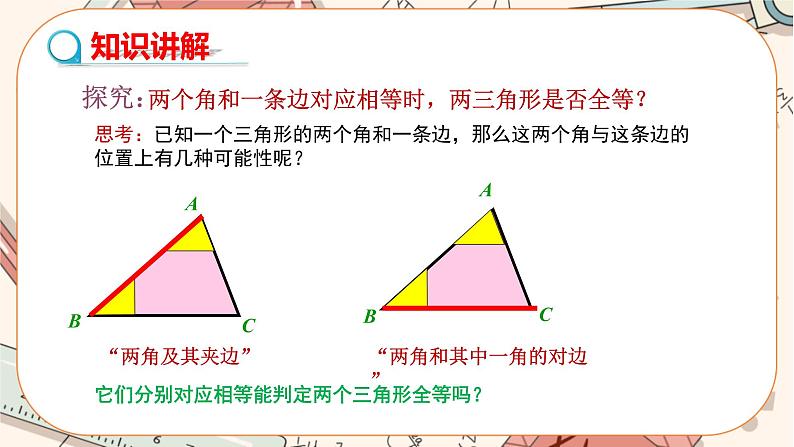
学习任务二　探究三角形全等的条件ASA

1.三角形中已知两角一边有几种可能？

(1)两角和它们的夹边；(2)　　         　　.

2.三角形的两个内角分别是60°和80°，它们的夹边为4 cm，你能画一个三角形同时满足这些条件吗？

将你画的三角形剪下来，与同伴比较，观察它们是不是全等，你能得出什么规律？

得到的规律：　　                                           　　.

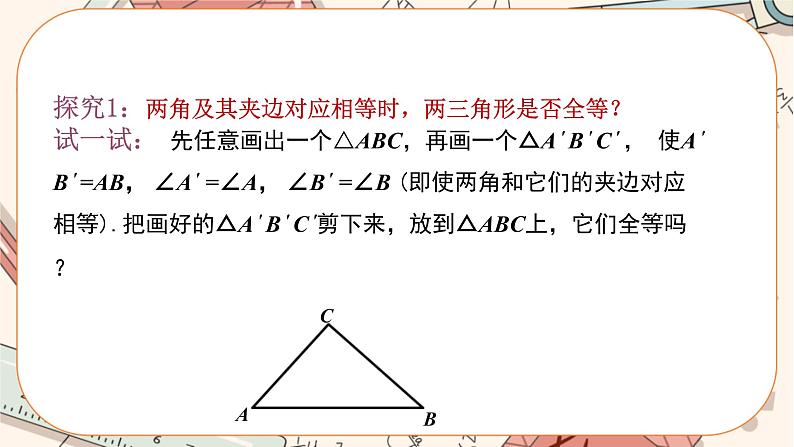
3.我们刚才作的三角形是一个特殊三角形，随意画一个△ABC，能不能作一个△A′B′C′，使∠A＝∠A′，∠B＝∠B′，AB＝A′B′呢？

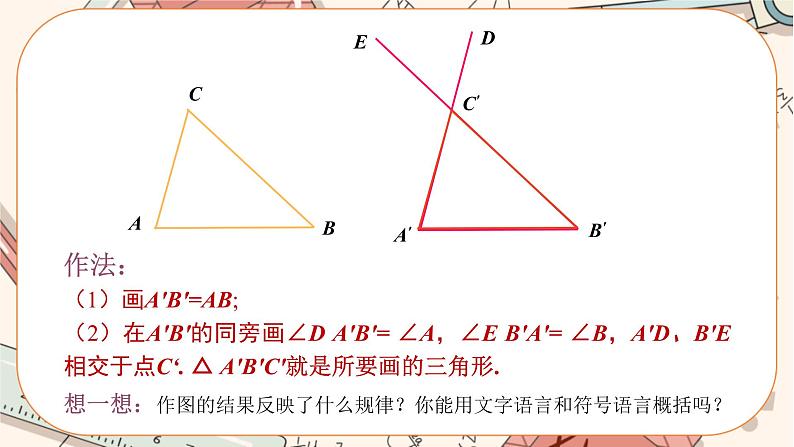
按下列步骤完成作图：(如图1)

图1

(1)先用量角器量出∠A与∠B的度数，再用直尺量出边AB的长；

(2)画线段A′B′，使A′B′＝AB；

(3)分别以A′，B′为顶点，A′B′为一边作∠DA′B′，∠EB′A′，使∠DA′B′＝∠CAB，∠EB′A′＝∠CBA.

(4)射线A′D与B′E交于一点，记为C′，即得到△A′B′C′.

将△A′B′C′剪下来，放在△ABC上，发现了什么？

发现的现象：　  　                                  　　.

总结：　　                                         　　.

学习任务三　探究三角形全等的条件AAS

思考：在一个三角形中两角确定，第三个角一定确定.我们是否可以不作图，用“ASA”推出“两角和其中一角的对边分别相等的两个三角形全等”呢？

如图2，在△ABC和△DEF中，∠A＝∠D，∠B＝ ∠E，BC＝EF，△ABC与△DEF全等吗？能利用角边角条件证明你的结论吗？

图2

证明：

总结：

合作探究

1.如图3，点D在AB上，点E在AC上，AB＝AC，∠B＝∠C.

图3

求证：AD＝AE.

分析：AD和AE分别在△ADC和△AEB中，所以要证AD＝AE，只需证明　　　　

≌　　　　.

证明：

2.如图4，AB⊥BC，AD⊥DC，∠1＝∠2，求证：AB＝AD.

图4

分析：要证明边相等，先证明两个三角形全等，即证明　　　　≌　　　　.

证明：

当堂达标

1.如图5，下列条件中，不能证明△ABC≌△DCB的是(　　)

A.AB＝DC，AC＝DB 

B.AB＝DC，∠ABC＝∠DCB

C.BO＝CO，∠A＝∠D 

D.AB＝DC，OA＝OD

图5　　　　　　 　图6

2.如图6，AD∥BC，∠B＝∠D，则　　　　≌　　　　，理由是　　　　.

3.如图7，线段AC与BD交于点O，且OA＝OC，若利用ASA证明△OAB ≌△OCD，则可添加的条件是　　　　；

若利用AAS证明△OAB≌△OCD，可添加的条件是　　　　　　　　.

图7

4.如图8，AB平分∠CAD，∠1＝∠2.求证：△AEC≌△AED.

     　　图8 　　　

5.如图9，AB∥CD，AE∥DF，BF＝CE，AE＝5，求DF的长.

     　图9　　　

课后提升

1.如图10，△ABC是等腰直角三角形，∠ACB＝90°，点D，C，E在同一直线上，且AD⊥DE于点D，BE⊥DE于点E.求证：△ADC≌△CEB.

       　图10　　

2.在△ABC中，AB＝AC，∠BAC＝90°，分别过点B，C向经过点A的直线EF作垂线，垂足为点E，F.

图11　　　　　　　　图12　　　　　　　　图13

(1)如图11，当EF与斜边BC不相交时，请探究EF，BE，CF之间的数量关系；

(2)如图12，当EF与斜边BC这样相交时，其他条件不变，请探究EF，BE，CF之间的数量关系；

(3)如图13，当EF与斜边BC这样相交时，其他条件不变，猜想EF，BE，CF之间的数量关系.

反思感悟

我的收获：

我的易错点：

参考答案

当堂达标

1.D　2.△ABC　△CDA　角角边(AAS)

3.∠A＝∠C或AB∥CD　∠B＝∠D或AB∥CD

4.证明：∵ AB平分∠CAD，∴ ∠CAE＝∠DAE.

∵ ∠1＝∠2，∠1+∠AEC＝∠2+∠AED，

∴ ∠AEC＝∠AED.

在△AEC和△AED中，

∴ △AEC≌△AED(ASA).

5.解：∵ BF＝CE，∴ BF-EF＝CE-EF，

∴ BE＝CF.

∵ AE∥DF，∴ ∠AEF＝∠DFE.

∵ ∠AEB+∠AEF＝∠DFC+∠DFE，

∴ ∠AEB＝∠DFC.

∵ AB∥CD，∴ ∠B＝∠C.

在△ABE和△DCF中，

∴ △ABE≌△DCF(ASA)，∴ AE＝DF.

∵ AE＝5，∴ DF＝5.

课后提升

1.证明：∵ △ABC是等腰直角三角形，

∴ ∠ACB＝90°，AC＝CB.

∴ ∠ACD+∠BCE＝90°.

又∵ AD⊥DC，∴ ∠ADC＝90°，

∴ ∠ACD+∠DAC＝90°，∴ ∠ECB＝∠DAC.

∵ BE⊥DE，∴ ∠CEB＝90°.

在△ADC和△CEB中，

∴ △ADC≌△CEB(AAS).

2.解：(1)∵ BE⊥EA，CF⊥AF，

∴ ∠BAC＝∠BEA＝∠CFE＝90°，

∴ ∠EAB+∠FAC＝90°，∠EBA+∠EAB＝90°，

∴ ∠FAC＝∠EBA.

在△ABE和△CAF中，

∴ △BEA≌△AFC(AAS)，

∴ EA＝FC，BE＝AF，

∴ EF＝EA+AF＝BE+CF.

(2)∵ BE⊥EA，CF⊥AF，

∴ ∠BAC＝∠BEA＝∠CFE＝90°，

∴ ∠EAB+∠CAF＝90°，∠ABE+∠EAB＝90°，

∴ ∠CAF＝∠ABE.

又∵ AB＝AC，∴ △BEA≌△AFC(AAS).

∴ BE＝AF，EA＝FC.

∵ EF＝AF-AE，∴ EF＝BE-CF.

(3)EF＝CF-BE.

理由：∵ BE⊥EA，CF⊥AF，

∴ ∠BAC＝∠BEA＝∠CFA＝90°，

∴ ∠EAB+∠CAF＝90°，∠ABE+∠EAB＝90°，

∴ ∠CAF＝∠ABE.

又∵ AB＝AC，∴ △BEA≌△AFC(AAS).

∴ EA＝FC，BE＝AF.

∵ EF＝EA-AF，∴ EF＝CF-BE.