高中数学第3章 圆锥曲线与方程3.2 双曲线精品ppt课件

这是一份高中数学第3章 圆锥曲线与方程3.2 双曲线精品ppt课件，共39页。PPT课件主要包含了学习目标，复习引入，新知学习，新知讲解，即时巩固，方法总结，方法技巧，课堂小结等内容，欢迎下载使用。
1.理解双曲线的简单几何性质（范围、对称性、顶点、渐近线、离心率）.2.掌握标准方程中a，b，c间的关系2.能用双曲线的简单几何性质解决一些简单的问题核心素养：直观想象、数学运算
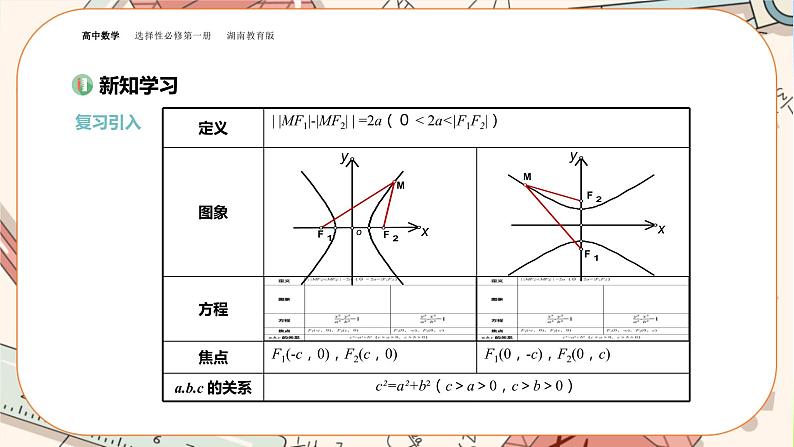
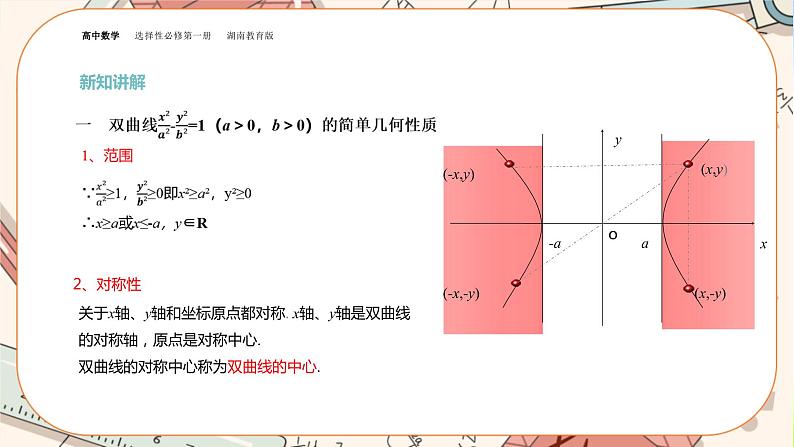
2、对称性
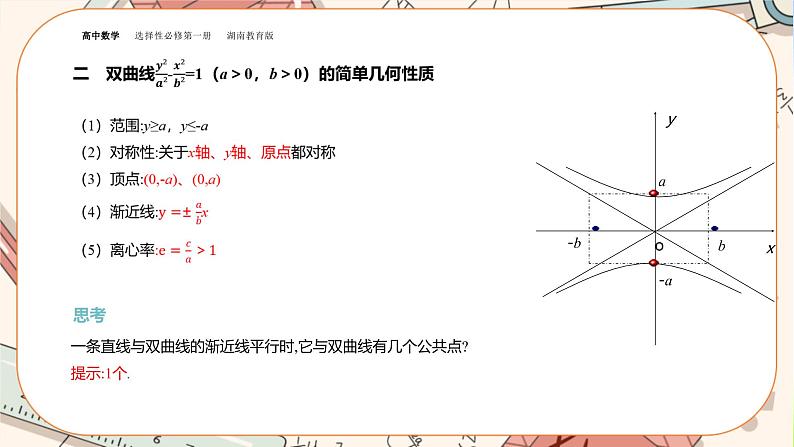
关于x轴、y轴和坐标原点都对称. x轴、y轴是双曲线的对称轴，原点是对称中心.双曲线的对称中心称为双曲线的中心.
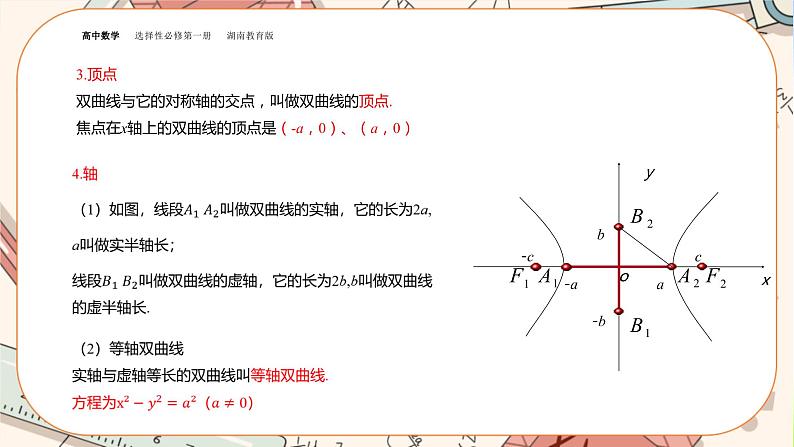
3.顶点双曲线与它的对称轴的交点，叫做双曲线的顶点.焦点在x轴上的双曲线的顶点是（-a，0）、（a，0）
（2）e的范围：因为c>a>0，所以双曲线的离心率e>1.
（3）e的含义：e是表示双曲线开口大小的一个量,e越大开口越大.
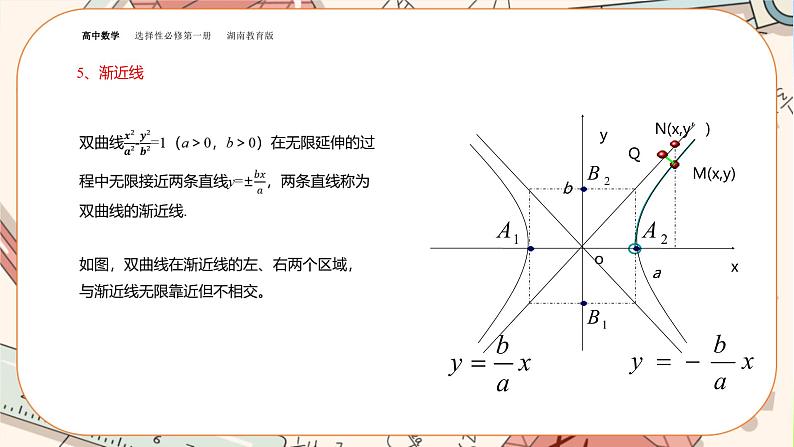
一条直线与双曲线的渐近线平行时,它与双曲线有几个公共点?提示:1个.
三　双曲线与椭圆的区别
四　直线与双曲线的位置关系位置关系直线与双曲线的三种位置关系
即时巩固 直线y=ax+1与双曲线3x2-y2=1相交于A，B两点.求线段AB的长.【解题提示】　联立直线与双曲线的方程，用“设而不求”的方法求解.
反思感悟由双曲线方程研究双曲线的几何性质，关键是求出a，b，c的值，如果已知方程不是标准方程，首先要化为标准方程，利用焦点在x2，y2两项中系数为正的坐标轴上可判断焦点的位置，利用焦点一定在实轴上确定a，b的值，再利用c2＝a2+b2确定c的值.
反思感悟 1.待定系数法求双曲线的标准方程具体过程是先定形 ，再定量.即先确定双曲线标准方程的形式，然后再根据a，b，c，e及渐近线方程之间的关系，求出a，b的值
2.巧设双曲线方程的六种方法与技巧(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
2.直线与双曲线的相交弦长问题
3. 双曲线的中点弦问题
1.知识清单： (1)双曲线的简单几何性质（范围、对称性、顶点、渐近线、离心率）.(2)双曲线与椭圆的几何性质的区别.(3)直线与双曲线的位置关系.2.方法归纳：数形结合、定义法、待定系数法.3.常见误区：忽略双曲线焦点位置，忽视离心率的取值范围