2023年安徽省教育教学联盟中考数学大联考密卷（一）（含答案）

这是一份2023年安徽省教育教学联盟中考数学大联考密卷（一）（含答案），共26页。试卷主要包含了选择题每小题都给出A，填空题等内容，欢迎下载使用。
2023年安徽省教育教学联盟中考数学大联考模拟卷
一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A、B、C、D四个选项，其中只有一个是符合题目要求的。
1．（4分）﹣2023的倒数是（　　）
A．2023 B．﹣2023 C． D．
2．（4分）2023年1月19日，安徽省统计局举行2022年全年全省经济运行情况新闻发布会．根据地区生产总值统一核算结果，全年全省生产总值达45045亿元，按不变价格计算，同比增长3.5%．数据45045亿用科学记数法表示为（　　）
A．450.45×1010 B．45.045×1011
C．4.5045×1012 D．4.5045×1013
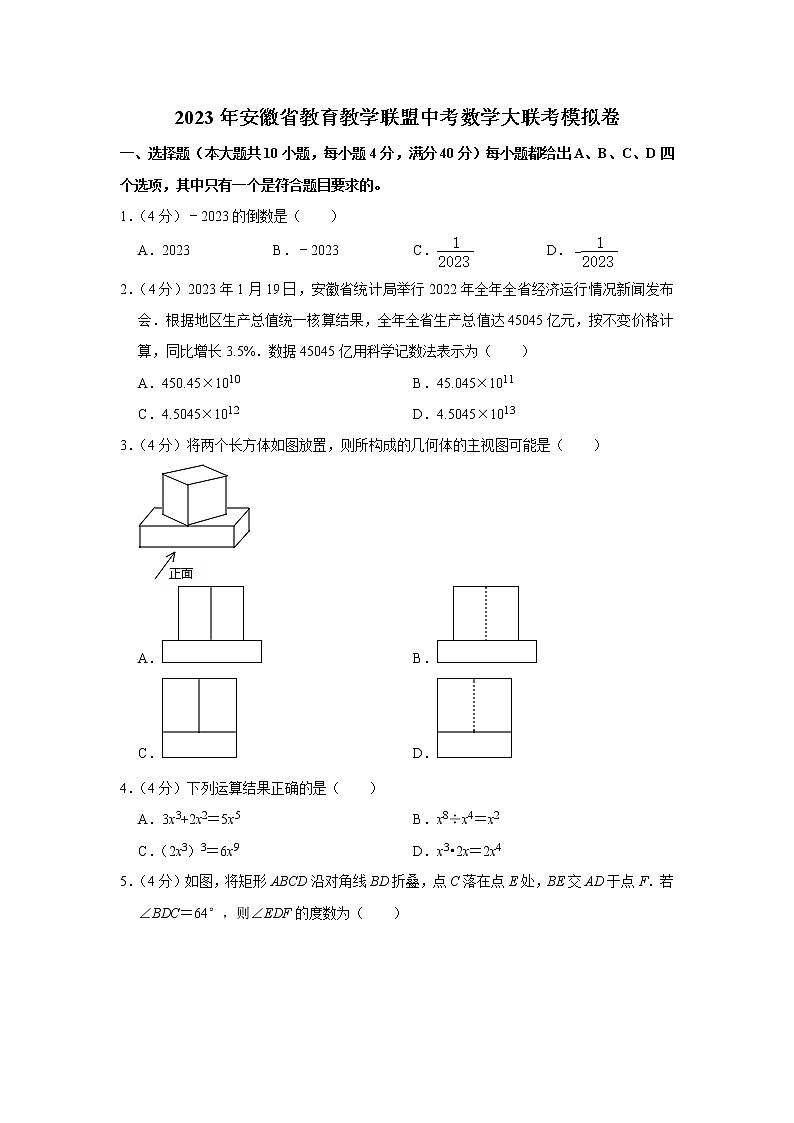
3．（4分）将两个长方体如图放置，则所构成的几何体的主视图可能是（　　）

A． B．
C． D．
4．（4分）下列运算结果正确的是（　　）
A．3x3+2x2＝5x5 B．x8÷x4＝x2
C．（2x3）3＝6x9 D．x3•2x＝2x4
5．（4分）如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F．若∠BDC＝64°，则∠EDF的度数为（　　）

A．36° B．38° C．41° D．44°
6．（4分）某市2022年国内生产总值（GDP）比2021年同期增长了12%，受各方面利好政策扶持，预计2023年比2022年增长17%．若这两年GDP的年平均增长率为x%，则x%满足的关系是（　　）
A．12%+17%＝x%
B．（1+12%）（1+17%）＝2（1+x%）
C．12%+17%＝2x
D．（1+12%）（1+17%）＝（1+x%）2
7．（4分）如图，在△ABC中，AB＝9，BC＝6，点D在边AB上，若∠BCD＝∠A，则线段AD的长是（　　）

A．4 B．5 C．6 D．9
8．（4分）甲、乙两位同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m，400m；田赛项目：跳远，跳高．甲、乙两位同学从5个项目中任选一个报名，恰好是一个径赛项目和一个田赛项目的概率是（　　）
A． B． C． D．
9．（4分）如图，⊙O的弦AB垂直于CD，点E为垂足，连接OE．若AE＝1，AB＝CD＝6，则OE的值是（　　）

A． B． C． D．
10．（4分）如图，点E，F，G，H分别是正方形ABCD的边DA，AB，BC，CD的中点，连接AH，BE，CF，DG，它们分别相交于点M，N，P，Q，连接NQ．若AB＝4，则下列结论错误的是（　　）

A．△ABE≌△DAH B．四边形MNPQ是正方形
C． D．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）不等式的解集为 　 　．
12．（5分）因式分解：y3+4y2+4y＝　 　．
13．（5分）如图，在平面直角坐标系中，直线y＝k1x+4与x轴交于点A，与y轴交于点C，与反比例函数y＝在第一象限内的图象交于点B，连接BO．若S△OBC＝4，tan∠BOC＝，则k2的值是 　 　．

14．（5分）在平面直角坐标系中，已知点P，Q的坐标分别为（﹣2，0），（2，2），抛物线y＝ax2﹣x+2（a≠0）也在该平面直角坐标系中．
（1）若该抛物线经过点P（﹣2，0），则此抛物线的对称轴为直线 　 　；
（2）若抛物线与线段PQ有两个不同的交点，则a的取值范围是 　 　．
三、（本大题共2小题，每小题8分，满分16分）
15．（8分）计算：（﹣1）2023+sin60°﹣|1﹣．
16．（8分）我国南宋数学家杨辉曾经提出这样的一个问题，“直田积，八百六十四，只云阔不及长十二步，问阔及长各几步”．大意：矩形田地的面积为864平方步，宽比长少12步，问矩形田地的长与宽各几步？（请你利用所学知识解决以上问题）
四、（本大题共2小题，每小题8分，满分16分）
17．（8分）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（2，3），B（1，1），C（3，2）．
（1）画出△ABC关于x轴对称的△A1B1C1（点A，B，C的对应点分别是点A1，B1，C1）；
（2）以点O为位似中心在第四象限内画出△A1B1C1的位似△A2B2C2，使得△A1B1C1与△A2B2C2的位似比为1：2．

18．（8分）仔细观察下列各式：
第1个等式：12+22+22＝（2+1）2；
第2个等式：22+62+32＝（6+1）2；
第3个等式：32+122+42＝（12+1）2；
请你根据以上规律，解决下列问题：
（1）写出第4个等式：　 　；
（2）写出第n（n为正整数）个等式，并证明等式成立．
五、（本大题共2小题，每小题10分，满分20分）
19．（10分）如图是一个山坡的纵向剖面图，坡面DE的延长线交地面AC于点B，点E恰好在BD的中点处，∠CBD＝60°，坡面AE的坡角为45°，山坡顶点D与水平线AC的距离，即CD的长为1000m．
（1）求BE的长度；
（2）求AB的长度．（结果保留根号）

20．（10分）如图，在△ABC中，∠B＝60°，以AB为直径的圆与BC边交于点D，过点D作DE⊥AC，垂足为点E，且DE是⊙O的切线．
（1）求证：△ABC为等边三角形；
（2）过点E作EF⊥AB，垂足为点F，连接DF．若AB＝2，求EF的长．

六、（本题满分12分）
21．（12分）某校为全校2500名学生提供了四种在线学习方式：在线阅读、在线听课、在线答疑、在线讨论，并对部分学生做了“最感兴趣的在线学习方式”调查（只选择一类），把调查结果绘制成两幅不完整的统计图，如下：

根据以上信息，解决下列问题：
（1）本次调查的人数为 　 　名，补全条形统计图；
（2）在扇形统计图中，“在线答疑”所在扇形的圆心角度数为 　 　；
（3）估计全校学生中有多少名学生喜欢“在线答疑”的方式．

七、（本题满分12分）
22．（12分）某重工机械公司为用户提供矿山机械设备，该设备每件的售价为18万元，每件的成本为y（万元）与月需求量x（件/月）满足关系式为常数），其中x＞0．经市场调研发现，月需求量x与月份n（n为整数，1≤n≤12）符合关系式x＝2n2﹣26n+144，且得到了下表中的部分数据．
月份n（月）
1
2
成本y（万元/件）
11
b
需求量x（件/月）
120
100
（1）求y与x满足的关系式，并求表中b的值；
（2）试推断是否存在某个月既无盈利也不亏损，请说明理由；
（3）设第n个月的利润为w（万元），请求出w与n的函数关系式，并求在这一年的前9个月中，哪个月的利润最大？最大利润是多少？
八、（本题满分14分）
23．（14分）在Rt△ACB和Rt△DCE中，∠ACB＝∠DCE＝90°，AC＝BC，CD＝CE．
（1）如图1，连接AE，BD，试写出AE与BD之间的关系：　 　；
（2）如图2，若点F，G分别是AB，DE的中点，连接FG，AE，求证：AE＝FG；
（3）如图3，连接AD，BE，点N为BE的中点，连接CN，求证：CN＝AD，CN⊥AD．



2023年安徽省教育教学联盟中考数学大联考模拟卷
（参考答案与详解）
一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A、B、C、D四个选项，其中只有一个是符合题目要求的。
1．（4分）﹣2023的倒数是（　　）
A．2023 B．﹣2023 C． D．
【解答】解：﹣2023的倒数是﹣．
故选：D．
2．（4分）2023年1月19日，安徽省统计局举行2022年全年全省经济运行情况新闻发布会．根据地区生产总值统一核算结果，全年全省生产总值达45045亿元，按不变价格计算，同比增长3.5%．数据45045亿用科学记数法表示为（　　）
A．450.45×1010 B．45.045×1011
C．4.5045×1012 D．4.5045×1013
【解答】解：45045亿＝4504500000000＝4.5045×1012．
故选：C．
3．（4分）将两个长方体如图放置，则所构成的几何体的主视图可能是（　　）

A． B．
C． D．
【解答】解：根据主视图的概念可知，从物体的正面看得到的视图是A，
故选：A．
4．（4分）下列运算结果正确的是（　　）
A．3x3+2x2＝5x5 B．x8÷x4＝x2
C．（2x3）3＝6x9 D．x3•2x＝2x4
【解答】解：A．3x3与2x2不是同类项，不能合并，因此选项A不符合题意；
B．x8÷x4＝x4，因此选项B不符合题意；
C．（2x3）3＝8x9，因此选项C不符合题意；
D．x3•2x＝2x4，因此选项D符合题意．
故选：D．
5．（4分）如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，BE交AD于点F．若∠BDC＝64°，则∠EDF的度数为（　　）

A．36° B．38° C．41° D．44°
【解答】解：∵四边形ABCD是矩形，
∴∠C＝90°，AD∥BC，
∵∠BDC＝64°，
∴∠DBC＝90°﹣∠BDC＝26°，
∵AD∥BC，
∴∠ADB＝∠DBC＝26°，
由折叠得：∠EDB＝∠BDC＝64°，
∴∠EDF＝∠EDB﹣∠ADB＝38°，
故选：B．
6．（4分）某市2022年国内生产总值（GDP）比2021年同期增长了12%，受各方面利好政策扶持，预计2023年比2022年增长17%．若这两年GDP的年平均增长率为x%，则x%满足的关系是（　　）
A．12%+17%＝x%
B．（1+12%）（1+17%）＝2（1+x%）
C．12%+17%＝2x
D．（1+12%）（1+17%）＝（1+x%）2
【解答】解：由题意得，（1+12%）（1+17%）＝（1+x%）2．
故选：D．
7．（4分）如图，在△ABC中，AB＝9，BC＝6，点D在边AB上，若∠BCD＝∠A，则线段AD的长是（　　）

A．4 B．5 C．6 D．9
【解答】解：∵∠BCD＝∠A，∠CBD＝∠ABC，
∴△BCD∽△BAC，
∴BD：BC＝BC：BA，
即BD：6＝6：9，
解得BD＝4，
∴AD＝AB﹣BD＝9﹣4＝5．
故选：B．
8．（4分）甲、乙两位同学报名参加校运动会，有以下5个项目可供选择：径赛项目：100m，200m，400m；田赛项目：跳远，跳高．甲、乙两位同学从5个项目中任选一个报名，恰好是一个径赛项目和一个田赛项目的概率是（　　）
A． B． C． D．
【解答】解：把径赛项目：100m，200m，400m，分别记为A、B、C；田赛项目：跳远，跳高，分别记为D、E，
画树状图如下：

共有25种等可能的结果，其中恰好是一个径赛项目和一个田赛项目的结果有12种，
∴恰好是一个径赛项目和一个田赛项目的概率为，
故选：C．

9．（4分）如图，⊙O的弦AB垂直于CD，点E为垂足，连接OE．若AE＝1，AB＝CD＝6，则OE的值是（　　）

A． B． C． D．
【解答】解：过O点作OH⊥AB于H点，OF⊥CD于F点，连接OB、OC，如图，则DF＝CF＝CD＝3，AH＝BH＝AB＝3，
∵AE＝1，
∴EH＝AH﹣AE＝2，
在Rt△OBH和Rt△OCF中，
，
∴Rt△OBH≌Rt△OCF（HL），
∴OH＝OF，
∵CD⊥AB，
∴∠HEF＝90°，
∵∠OHE＝∠OFE＝90°，
∴四边形OHEF为正方形，
∴OE＝EH＝2．
故选：A．

10．（4分）如图，点E，F，G，H分别是正方形ABCD的边DA，AB，BC，CD的中点，连接AH，BE，CF，DG，它们分别相交于点M，N，P，Q，连接NQ．若AB＝4，则下列结论错误的是（　　）

A．△ABE≌△DAH B．四边形MNPQ是正方形
C． D．
【解答】解：∵四边形ABCD是正方形，
∴AB＝BC＝CD＝AD，
∠BAD＝∠ABC＝∠BCD＝∠ADC＝90°，
∵点F、G、H、E分别是正方形边AB、BC、CD、DA的中点，
∴AF∥CH，AF＝CH，
∴四边形AFCH是平行四边形，
同理可得四边形BEDG是平行四边形，
∴AH∥CF，BE∥DG，
∴四边形MNPQ是平行四边形，
∵AB＝AD，∠BAD＝∠ADC，AE＝DH，
∴△ABE≌△DAH（SAS），故A正确；
∴∠ABE＝∠DAH，
∴∠ABE+∠BAM＝∠DAH+∠BAM＝90°，
∴∠BMA＝∠NMQ＝90°，
∴平行四边形MNPQ是矩形，
由△ABM≌△DQ（AAS）
∴BM＝AQ，
由△AEM≌△BFN（AAS）
∴AM＝BN，MN＝MQ，
∴矩形MNPQ是正方形，故B正确；
∵BF＝AE＝DH＝CG＝2，
根据勾股定理，得
∴BE＝DG＝＝＝2，
由△BFN∽△BEA，
∴＝，
解得FN＝，故C正确；
∴EM＝FN＝，
∴BN＝＝，
∴MN＝BE﹣BN﹣EM＝，
∴QN＝MN＝，故D错误；
故选：D．
二、填空题（本大题共4小题，每小题5分，满分20分）
11．（5分）不等式的解集为 　x＜4　．
【解答】解：，
去分母得，x﹣1＜3，
移项得，x＜1+3，
合并同类项得，x＜4．
故答案为：x＜4．
12．（5分）因式分解：y3+4y2+4y＝　y（y+2）2　．
【解答】解：原式＝y（y2+4y+4）＝y（y+2）2，
故答案为：y（y+2）2．
13．（5分）如图，在平面直角坐标系中，直线y＝k1x+4与x轴交于点A，与y轴交于点C，与反比例函数y＝在第一象限内的图象交于点B，连接BO．若S△OBC＝4，tan∠BOC＝，则k2的值是 　16　．

【解答】解：∵直线y＝k1x+4与x轴交于点A，与y轴交于点C，作BD⊥y轴交于点D，
∴点C的坐标为（0，4），
∴OC＝4，
∵S△OBC＝4，
∴BD＝2，
∵tan∠BOC＝，
∴＝，
∴OD＝8，
∴点B的坐标为（2，8），
∵反比例函数y＝在第一象限内的图象交于点B，
∴k2＝2×8＝16．

14．（5分）在平面直角坐标系中，已知点P，Q的坐标分别为（﹣2，0），（2，2），抛物线y＝ax2﹣x+2（a≠0）也在该平面直角坐标系中．
（1）若该抛物线经过点P（﹣2，0），则此抛物线的对称轴为直线 　x＝﹣　；
（2）若抛物线与线段PQ有两个不同的交点，则a的取值范围是 　≤a＜或a≤﹣1　．
【解答】解：（1）∵抛物线y＝ax2﹣x+2（a≠0）经过点P（﹣2，0），
∴4a+2+2＝0，
∴a＝﹣1，
∴y＝﹣x2﹣x+2，
∴抛物线的对称轴为直线x＝﹣＝﹣，
故答案为：x＝﹣；
（2）设直线PQ为y＝kx+b，
将点P（﹣2，0），Q（2，2）代入得，
解得，
∴直线PQ：y＝x+1，
抛物线与直线PQ有两个交点，即方程ax2﹣x+2＝x+1有解，
化简得：2ax2﹣3x+2＝0，
∴Δ＝b2﹣4ac＝9﹣16a＞0，
解得a＜，
①当0＜a＜时，如图，

抛物线过定点（0，2），
当经过点Q（2，2）时，
代入点Q得4a﹣2+2＝2，
解得a＝，
故a的取值范围≤a＜；
②当a＜0时，如图，

抛物线过定点（0，2），
当抛物线经过点P（﹣2，0）时，
代入点P得4a+2+2＝0，
解得a＝﹣1，
故a的取值范围a≤﹣1；
综上所述，抛物线与线段PQ有两个不同的交点，a的取值范围≤a＜或a≤﹣1．
故答案为：≤a＜或a≤﹣1．


三、（本大题共2小题，每小题8分，满分16分）
15．（8分）计算：（﹣1）2023+sin60°﹣|1﹣．
【解答】解：（﹣1）2023+sin60°﹣|1﹣
＝﹣1+﹣（﹣1）
＝﹣1+﹣+1
＝﹣．
16．（8分）我国南宋数学家杨辉曾经提出这样的一个问题，“直田积，八百六十四，只云阔不及长十二步，问阔及长各几步”．大意：矩形田地的面积为864平方步，宽比长少12步，问矩形田地的长与宽各几步？（请你利用所学知识解决以上问题）
【解答】解：设矩形田地的宽为x步，则长为（x+12）步，
依题意得：（x+12）x＝864，
整理得：x2+12x﹣864＝0，
解得：x1＝24，x2＝﹣36（不合题意，舍去），
∴x+12＝24+12＝36．
答：矩形田地的长为36步，宽为24步．
四、（本大题共2小题，每小题8分，满分16分）
17．（8分）如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（2，3），B（1，1），C（3，2）．
（1）画出△ABC关于x轴对称的△A1B1C1（点A，B，C的对应点分别是点A1，B1，C1）；
（2）以点O为位似中心在第四象限内画出△A1B1C1的位似△A2B2C2，使得△A1B1C1与△A2B2C2的位似比为1：2．

【解答】解：（1）如图△A1B1C1，即为所求.
（2）如图，△A2B2C2即为所求．

18．（8分）仔细观察下列各式：
第1个等式：12+22+22＝（2+1）2；
第2个等式：22+62+32＝（6+1）2；
第3个等式：32+122+42＝（12+1）2；
请你根据以上规律，解决下列问题：
（1）写出第4个等式：　42+202+52＝（20+1）2　；
（2）写出第n（n为正整数）个等式，并证明等式成立．
【解答】解：（1）由题意可得，第4个等式为：42+202+52＝（20+1）2；
故答案为：42+202+52＝（20+1）2；
（2）第n个等式为：n2+[n（n+1）]2+（n+1）2＝[n（n+1）+1]2，
右边＝[n（n+1）]2+2n（n+1）+1
＝[n（n+1）]2+2n2+2n+1
＝[n（n+1）]2+n2+（n2+2n+1）
＝n2+[n（n+1）]2+（n+1）2
＝左边，
故等式成立．
五、（本大题共2小题，每小题10分，满分20分）
19．（10分）如图是一个山坡的纵向剖面图，坡面DE的延长线交地面AC于点B，点E恰好在BD的中点处，∠CBD＝60°，坡面AE的坡角为45°，山坡顶点D与水平线AC的距离，即CD的长为1000m．
（1）求BE的长度；
（2）求AB的长度．（结果保留根号）

【解答】解：（1）过点E作EF⊥AC于点F.
∵点E为BD的中点，
∴EF＝＝m，
在Rt△BEF中，sin∠EBF＝sin60°＝＝，
解得BE＝1000，
经检验，BE＝1000是原方程的解且符合题意，
∴BE的长度为1000m．
（2）在Rt△AEF中，∠EAF＝45°，
∴AF＝EF＝500m，
在Rt△BEF中，tan∠EBF＝tan60°＝，
解得BF＝500，
经检验，BF＝500是原方程的解且符合题意，
∴AB＝AF﹣BF＝（﹣500）m．
∴AB的长度为（﹣500）m．

20．（10分）如图，在△ABC中，∠B＝60°，以AB为直径的圆与BC边交于点D，过点D作DE⊥AC，垂足为点E，且DE是⊙O的切线．
（1）求证：△ABC为等边三角形；
（2）过点E作EF⊥AB，垂足为点F，连接DF．若AB＝2，求EF的长．

【解答】（1）证明：连接OD，如图，
∵OB＝OD，∠B＝60°，
∴△OBD为等边三角形，
∴∠BOD＝∠BDO＝60°，
∵DE是⊙O的切线，
∴OD⊥DE，
∵DE⊥AC，
∴OD∥AC，
∴∠A＝∠BOD＝60°，∠C＝∠BDO＝60°，
∴△ABC为等边三角形；
（2）解：∵△ABC为等边三角形，OA＝OB＝1，
∴AC＝BC＝2，
∵△OBD为等边三角形，
∴BD＝OB＝1，
∴CD＝1，
在Rt△CDE中，∵∠C＝60°，
∴CE＝CD＝，
∴AE＝AC﹣CE＝，
在Rt△AEF中，∵∠A＝60°，
∴AF＝AE＝，
∴EF＝AF＝．

六、（本题满分12分）
21．（12分）某校为全校2500名学生提供了四种在线学习方式：在线阅读、在线听课、在线答疑、在线讨论，并对部分学生做了“最感兴趣的在线学习方式”调查（只选择一类），把调查结果绘制成两幅不完整的统计图，如下：

根据以上信息，解决下列问题：
（1）本次调查的人数为 　250　名，补全条形统计图；
（2）在扇形统计图中，“在线答疑”所在扇形的圆心角度数为 　108°　；
（3）估计全校学生中有多少名学生喜欢“在线答疑”的方式．

【解答】解：（1）本次调查的人数为：50÷20%＝250（名），
在线答疑的人数为：250﹣50﹣100﹣25＝75（名），
补全条形统计图如下：

故答案为：250；
（2）“在线答疑”所在扇形的圆心角度数为：360°×＝108°．
故答案为：108°；
（3）2500×＝750（名），
答：估计全校学生中有750名学生喜欢“在线答疑”的方式．
七、（本题满分12分）
22．（12分）某重工机械公司为用户提供矿山机械设备，该设备每件的售价为18万元，每件的成本为y（万元）与月需求量x（件/月）满足关系式为常数），其中x＞0．经市场调研发现，月需求量x与月份n（n为整数，1≤n≤12）符合关系式x＝2n2﹣26n+144，且得到了下表中的部分数据．
月份n（月）
1
2
成本y（万元/件）
11
b
需求量x（件/月）
120
100
（1）求y与x满足的关系式，并求表中b的值；
（2）试推断是否存在某个月既无盈利也不亏损，请说明理由；
（3）设第n个月的利润为w（万元），请求出w与n的函数关系式，并求在这一年的前9个月中，哪个月的利润最大？最大利润是多少？
【解答】解：（1）把x＝120，y＝11代入y＝6+得：11＝6+，
解得a＝600，
∴y与x满足的关系式为y＝6+，
当x＝100时，y＝6+＝12，
∴b＝﹣12；
（2）不存在某个月既无盈利也不亏损，理由：
假设存在某个月既无盈利也不亏损，
则x[18﹣（6+）＝0，
解得x＝50，
∴2n2﹣26n+144＝50，
整理得：n2﹣13n+47＝0，
∵Δ＝（﹣13）2﹣4×47＝169﹣188＝﹣19＜0，
∴方程无解，
∴不存在某个月既无盈利也不亏损；
（3）根据题意得：w＝x（18﹣y）
＝x（18﹣6﹣）
＝12x﹣600
＝12（2n2﹣26n+144）﹣600
＝24n2﹣312n+1128
＝24（n﹣6.5）2+114，
∵24＞0，
∴当1≤n≤6时，w随n的增大而减小，当n＝1时，w最大值为840，
当7≤n≤9时，w随n的增大而增大，当n＝9时，w最大值为264，
∵840＞264，
∴在这一年的前9个月中，1月的利润最大，最大利润是840万元．
八、（本题满分14分）
23．（14分）在Rt△ACB和Rt△DCE中，∠ACB＝∠DCE＝90°，AC＝BC，CD＝CE．
（1）如图1，连接AE，BD，试写出AE与BD之间的关系：　AE＝BD，AE⊥BD　；
（2）如图2，若点F，G分别是AB，DE的中点，连接FG，AE，求证：AE＝FG；
（3）如图3，连接AD，BE，点N为BE的中点，连接CN，求证：CN＝AD，CN⊥AD．


【解答】（1）解：结论：AE＝BE，AE⊥BD．
理由：如图1中，设AE交BC于点O，AE交BD于点T．

∵∠ACB＝∠DCE＝90°，
∴∠ACE＝∠BCD，
在△ACE和△BCD中，
，
∴△ACE≌△BCD（SAS），
∴AE＝BD，∠CAE＝∠CBD，
∵∠CAO+∠AOC＝90°，∠AOC＝∠BOT，
∴∠CBD+∠NOT＝90°，
∴∠ATB＝90°，
∴AE⊥BD．
故答案为：AE＝BD，AE⊥BD；

（2）证明：连接CG，CF．

∵△ACB，△DCE都是等腰直角三角形，AF＝FB，DG＝GE，
∴∠BCF＝∠ACF＝45°，∠GCE＝∠GCD＝45°，
∴∠GCF＝∠BCF+∠ECB+∠GCE＝90°+∠ECB，
∵∠ACE＝90°+∠ECB，
∴∠ACE＝∠FCG，
∵＝＝，
∴△ACE∽△BCG，
∴＝＝，
∴AE＝FG；

（3）证明：延长CN到T，使得CN＝NT，连接ET，BT．

∵CN＝NT，EN＝NB，
∴四边形BCET是平行四边形，
∴BC＝ET，BC∥ET，
∴∠BCE+∠CET＝180°，
∵∠DCA+∠BCE＝180°，
∴∠DCA＝∠CET，
∵CD＝CE，CA＝CB＝ET，
∴△DCA≌△CET（SAS），
∴DA＝CT，∠DAC＝∠CTE，
∵CN＝CT，
∴CN＝AD，
∵BC∥ET，
∴∠BCT＝∠ETC，
∵∠ACK+∠BCT＝90°，
∴∠DAC+∠ACK＝90°，
∴∠AKC＝90°，
∴CT⊥AD．