备战中考数理化——中考数学模拟试卷 (9)（含答案）

这是一份备战中考数理化——中考数学模拟试卷 (9)（含答案），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
备战中考数理化——中考数学模拟试卷9（含答案）

一、选择题（满分16分，每小题2分）
1．（2分）下列说法不正确的是（　　）
A．三角形的三条高线交于一点
B．直角三角形有三条高
C．三角形的三条角平分线交于一点
D．三角形的三条中线交于一点
2．（2分）若代数式有意义，则x的取值范围是（　　）
A．x＞﹣1且 x≠1 B．x≥﹣1 C．x≠1 D．x≥﹣1且 x≠1
3．（2分）如图是由几个相同的正方体搭成的一个几何体，从正面看到的平面图形是（　　）

A． B．
C． D．
4．（2分）如图，直线AB∥CD，则下列结论正确的是（　　）

A．∠1＝∠2 B．∠3＝∠4 C．∠1+∠3＝180° D．∠3+∠4＝180°
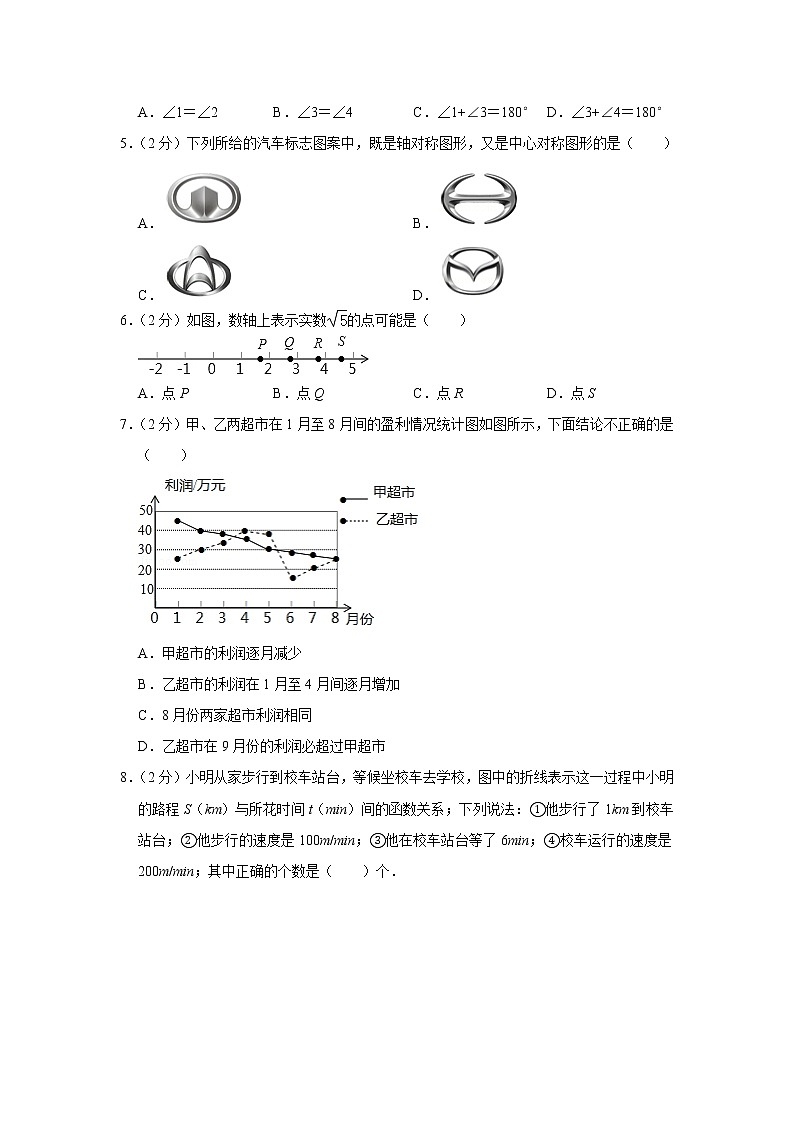
5．（2分）下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（　　）
A． B．
C． D．
6．（2分）如图，数轴上表示实数的点可能是（　　）

A．点P B．点Q C．点R D．点S
7．（2分）甲、乙两超市在1月至8月间的盈利情况统计图如图所示，下面结论不正确的是（　　）

A．甲超市的利润逐月减少
B．乙超市的利润在1月至4月间逐月增加
C．8月份两家超市利润相同
D．乙超市在9月份的利润必超过甲超市
8．（2分）小明从家步行到校车站台，等候坐校车去学校，图中的折线表示这一过程中小明的路程S（km）与所花时间t（min）间的函数关系；下列说法：①他步行了1km到校车站台；②他步行的速度是100m/min；③他在校车站台等了6min；④校车运行的速度是200m/min；其中正确的个数是（　　）个．

A．1 B．2 C．3 D．4
二、填空题（满分16分，每小题2分）
9．（2分）若△ABC∽△DEF，请写出 2 个不同类型的正确的结论　 　、　 　．
10．（2分）把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A，且另三个锐角顶点B，C，D在同一直线上．若AB＝，则CD＝　 　．

11．（2分）化简：＝　 　．
12．（2分）你喜欢足球吗？下面是对某学校七年级学生的调查结果：

男同学
女同学
喜欢的人数
75
24
不喜欢的人数
15
36
则男同学中喜欢足球的人数占全体同学的百分比是　 　．
13．（2分）如图，AB是⊙O的直径，C是⊙O上的点，过点C作⊙O的切线交AB的延长线于点D．若∠A＝32°，则∠D＝　 　度．

14．（2分）A，B两市相距200千米，甲车从A市到B市，乙车从B市到A市，两车同时出发，已知甲车速度比乙车速度快15千米/小时，且甲车比乙车早半小时到达目的地．若设乙车的速度是x千米/小时，则根据题意，可列方程　 　．
15．（2分）如图，线段AB＝4，M为AB的中点，动点P到点M的距离是1，连接PB，线段
PB绕点P逆时针旋转90°得到线段PC，连接AC，则线段AC长度的最大值是　 　．

16．（2分）阅读下面材料：
在数学课上，老师提出如下问题：
尺规作图：作Rt△ABC，使其斜边AB＝c，一条直角边BC＝a．
已知线段a，c如图．
小芸的作法如下：
①取AB＝c，作AB的垂直平分线交AB于点O；
②以点O为圆心，OB长为半径画圆；
③以点B为圆心，a长为半径画弧，与⊙O交于点C；
④连接BC，AC．
则Rt△ABC即为所求．
老师说：“小芸的作法正确．”
请回答：小芸的作法中判断∠ACB是直角的依据是　 　．

三、解答题（共12小题，满分0分）
17．计算：（）﹣2﹣+（﹣4）0﹣cos45°．
18．解不等式组
19．如图，△ABC中，∠A＝30°，∠B＝62°，CE平分∠ACB．
（1）求∠ACE；
（2）若CD⊥AB于点D，∠CDF＝74°，证明：△CFD是直角三角形．

20．如图，已知反比例函数y＝的图象与一次函数y＝x+b的图象交于点A（1，4），点B（﹣4，n）．
（1）求n和b的值；
（2）求△OAB的面积；
（3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．

21．如图，已知AC是矩形ABCD的对角线，AC的垂直平分线EF分别交BC、AD于点E和F，EF交AC于点O．
（1）求证：四边形AECF是菱形；
（2）若AC＝8，EF＝6，求BC的长．

22．已知关于x的方程x2﹣2mx+m2+m﹣2＝0有两个不相等的实数根．
（1）求m的取值范围．
（2）当m为正整数时，求方程的根．
23．如图，AB为⊙O的直径，C为⊙O上一点，经过点C的切线交AB的延长线于点E，AD⊥EC交EC的延长线于点D，AD交⊙O于F，FM⊥AB于H，分别交⊙O、AC于M、N，连接MB，BC．
（1）求证：AC平分∠DAE；
（2）若cosM＝，BE＝1，①求⊙O的半径；②求FN的长．

24．某商场甲、乙两名业务员10个月的销售额（单位：万元）如下：
甲
7.2；9.6；9.6；7.8；9.3；4.6；6.5；8.5；9.9；9.6
乙
5.8；9.7；9.7；6.8；9.9；6.9；8.2；6.7；8.6；9.7
根据上面的数据，将下表补充完整：

4.0≤x≤4.9
5.0≤x≤5.9
6.0≤x≤6.9
7.0≤x≤7.9
8.0≤x≤8.9
9.0≤x≤10.0
甲
1
0
1
2
1
5
乙
　 　
　 　
　 　
　 　
　 　
　 　
（说明：月销售额在8.0万元及以上可以获得奖金，7.0～7.9万元为良好，6.0～6.9万元为合格，6.0万元以下为不合格）
两组样本数据的平均数、中位数、众数如表所示：
人员
平均数（万元）
中位数（万元）
众数（万元）
甲
8.2
8.9
9.6
乙
8.2
8.4
9.7
结论 （1）估计乙业务员能获得奖金的月份有　 　个；
（2）可以推断出　 　业务员的销售业绩好，理由为　 　．（至少从两个不同的角度说明推断的合理性）
25．如图，在△ABC中，∠C＝60°，BC＝3厘米，AC＝4厘米，点P从点B出发，沿B→C→A以每秒1厘米的速度匀速运动到点A．设点P的运动时间为x秒，B、P两点间的距离为y厘米．
小新根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小新的探究过程，请补充完整：
（1）通过取点、画图、测量，得到了x与y的几组值，如下表：
x（s）
0
1
2
3
4
5
6
7
y（cm）
0
1.0
2.0
3.0
2.7
2.7
m
3.6
经测量m的值是　 　（保留一位小数）．
（2）建立平面直角坐标系，描出表格中所有各对对应值为坐标的点，画出该函数的图象；
（3）结合画出的函数图象，解决问题：在曲线部分的最低点时，在△ABC中画出点P所在的位置．

26．有一个二次函数满足以下条件：①函数图象与x轴的交点坐标分别为A（1，0），B（x2，y2）（点B在点A的右侧）；②对称轴是x＝3；③该函数有最小值是﹣2．
（1）请根据以上信息求出二次函数表达式；
（2）将该函数图象中x＞x2部分的图象向下翻折与原图象未翻折的部分组成图象“G”，试结合图象分析：平行于x轴的直线y＝m与图象“G”的交点的个数情况．

27．在△ABC中，AB＝BC＝2，∠ABC＝120°，将△ABC绕点B顺时针旋转角α（0＜α＜120°），得△A1BC1，交AC于点E，AC分别交A1C1、BC于D、F两点．

（1）如图①，观察并猜想，在旋转过程中，线段EA1与FC有怎样的数量关系？并证明你的结论；
（2）如图②，当α＝30°时，试判断四边形BC1DA的形状，并说明理由；
（3）在（2）的情况下，求ED的长．
28．如图，已知一次函数y＝x+4与x轴交于点A，与y轴交于点C，一次函数y＝﹣x+b经过点C与x轴交于点B．
（1）求直线BC的解析式；
（2）点P为x轴上方直线BC上一点，点G为线段BP的中点，点F为线段AB的中点，连接GF，取GF的中点M，射线PM交x轴于点H，点D为线段PH的中点，点E为线段AH的中点，连接DE，求证：DE＝GF；
（3）在（2）的条件下，延长PH至Q，使PM＝MQ，连接AQ、BM，若∠BAQ+∠BMQ＝∠DEB，求点P的坐标．


2020年中考数学模拟试卷
参考答案与试题解析
一、选择题（满分16分，每小题2分）
1．【解答】解：A、三角形的三条高线所在的直线不一定交于一点，错误；
B、直角三角形有三条高，正确；
C、三角形的三条角平分线交于一点，正确；
D、三角形的三条中线交于一点，正确；
故选：A．
2．【解答】解：由题意得：x+1≥0，且x﹣1≠0，
解得：x≥﹣1，且x≠1，
故选：D．
3．【解答】解：从正面看第一层是三个小正方形，第二层在中间位置一个小正方形，故D符合题意，
故选：D．
4．【解答】解：如图，∵AB∥CD，
∴∠3+∠5＝180°，
又∵∠5＝∠4，
∴∠3+∠4＝180°，
故选：D．

5．【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；
B、既是轴对称图形，又是中心对称图形，故本选项正确；
C、是轴对称图形，不是中心对称图形，故本选项错误；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选：B．
6．【解答】解：∵2＜＜3，
∴数轴上表示实数的点可能是点Q．
故选：B．
7．【解答】解：A、甲超市的利润逐月减少，此选项正确；
B、乙超市的利润在1月至4月间逐月增加，此选项正确；
C、8月份两家超市利润相同，此选项正确；
D、乙超市在9月份的利润不一定超过甲超市，此选项错误；
故选：D．
8．【解答】解：根据题意得：
小明用了10分钟步行了1km到校站台，
即小明步行了1km到校车站台，①正确，
1000÷10＝100m/min，
即他步行的速度是100m/min，②正确，
小明在校车站台从第10min等到第16min，
即他在校车站台等了6min，③正确，
小明用了14min的时间坐校车，走了7km的路程，
7000÷14＝500m/min，
即校车运行的速度是500m/min，④不正确，
即正确的是①②③，
故选：C．
二、填空题（满分16分，每小题2分）
9．【解答】解：∵△ABC∽△DEF，
∴∠ABC＝∠DEF，＝＝，
故答案为：∠ABC＝∠DEF；＝＝．
10．【解答】解：如图，过点A作AF⊥BC于F，
在Rt△ABC中，∠B＝45°，
∴BC＝AB＝2，BF＝AF＝AB＝1，
∵两个同样大小的含45°角的三角尺，
∴AD＝BC＝2，
在Rt△ADF中，根据勾股定理得，DF＝＝
∴CD＝BF+DF﹣BC＝1+﹣2＝﹣1，
故答案为：﹣1．

11．【解答】解：原式＝＝，
故答案为：．
12．【解答】解：由题可得，男同学中喜欢足球的人数占全体同学的百分比是：
×100%＝50%，
故答案为：50%．
13．【解答】解：连接OC，
由圆周角定理得，∠COD＝2∠A＝64°，
∵CD为⊙O的切线，
∴OC⊥CD，
∴∠D＝90°﹣∠COD＝26°，
故答案为：26．

14．【解答】解：设乙车的速度是x千米/小时，则根据题意，可列方程：
﹣＝．
故答案为：﹣＝．
15．【解答】解：如图所示：过点C作CD⊥y轴，垂足为D，过点P作PE⊥DC，垂足为E，延长EP交x轴于点F．

∵AB＝4，O为AB的中点，
∴A（﹣2，0），B（2，0）．
设点P的坐标为（x，y），则x2+y2＝1．
∵∠EPC+∠BPF＝90°，∠EPC+∠ECP＝90°，
∴∠ECP＝∠FPB．
由旋转的性质可知：PC＝PB．
在△ECP和△FPB中，
，
∴△ECP≌△FPB．
∴EC＝PF＝y，FB＝EP＝2﹣x．
∴C（x+y，y+2﹣x）．
∵AB＝4，O为AB的中点，
∴AC＝＝．
∵x2+y2＝1，
∴AC＝．
∵﹣1≤y≤1，
∴当y＝1时，AC有最大值，AC的最大值为＝3．
故答案为：3．
16．【解答】解：小芸的作法中判断∠ACB是直角的依据是直径所对的圆周角为直角．
故答案为直径所对的圆周角为直角．
三、解答题（共12小题，满分0分）
17．【解答】解：原式＝4﹣3+1﹣×
＝2﹣1
＝1．
18．【解答】解：解不等式2x+1≥﹣1，得：x≥﹣1，
解不等式x+1＞4（x﹣2），得：x＜3，
则不等式组的解集为﹣1≤x＜3．
19．【解答】解：（1）∵∠A＝30°，∠B＝62°，
∴∠ACB＝180°﹣∠A﹣∠B＝88°，
∵CE平分∠ACB，
∴∠ACE＝∠BCE＝∠ACB＝44°；

（2）∵CD⊥AB，
∴∠CDB＝90°，
∴∠BCD＝90°﹣∠B＝28°，
∴∠FCD＝∠ECB﹣∠BCD＝16°，
∵∠CDF＝74°，
∴∠CFD＝180°﹣∠FCD﹣∠CDF＝90°，
∴△CFD是直角三角形．
20．【解答】解：（1）把A点（1，4）分别代入反比例函数y＝，一次函数y＝x+b，
得k＝1×4，1+b＝4，
解得k＝4，b＝3，
∵点B（﹣4，n）也在反比例函数y＝的图象上，
∴n＝＝﹣1；

（2）如图，设直线y＝x+3与y轴的交点为C，
∵当x＝0时，y＝3，
∴C（0，3），
∴S△AOB＝S△AOC+S△BOC＝×3×1+×3×4＝7.5；

（3）∵B（﹣4，﹣1），A（1，4），
∴根据图象可知：当x＞1或﹣4＜x＜0时，一次函数值大于反比例函数值．

21．【解答】（1）证明：∵四边形ABCD是矩形
∴AD∥BC，
∴∠DAC＝∠ACB，
∵EF垂直平分AC，
∴AF＝FC，AE＝EC，
∴∠FAC＝∠FCA，
∴∠FCA＝∠ACB，
∵∠FCA+∠CFE＝90°，∠ACB+∠CEF＝90°，
∴∠CFE＝∠CEF，
∴CE＝CF，
∴AF＝FC＝CE＝AE，
∴四边形AECF是菱形．

证法二：∵四边形ABCD是矩形
∴AD∥BC，
∴∠DAC＝∠ACB，∠AFO＝∠CEO，
∵EF垂直平分AC，
∴OA＝OC，
∴△AOF≌△COE，
∴OE＝OF，
∴四边形AECF是平行四边形，
∵AC⊥EF，
∴四边形AECF是菱形．

（2）解：∵四边形AECF是菱形
∴OC＝AC＝4，OE＝EF＝3
∴CE＝＝＝5，
∵∠COE＝∠ABC＝90，∠OCE＝∠BCA，
∴△COE∽△CBA，
∴＝，
∴＝，
∴BC＝．

22．【解答】解：（1）∵关于x的方程x2﹣2mx+m2+m﹣2＝0有两个不相等的实数根，
∴△＝（﹣2m）2﹣4（m2+m﹣2）＞0．
解得m＜2；

（2）由（1）知，m＜2．
有m为正整数，
∴m＝1，
将m＝1代入原方程，得
x2﹣2x＝0
x（x﹣2）＝0，
解得x1＝0，x2＝2．
23．【解答】（1）证明：连接OC，如图，
∵直线DE与⊙O相切于点C，
∴OC⊥DE，
又∵AD⊥DE，
∴OC∥AD．
∴∠1＝∠3
∵OA＝OC，
∴∠2＝∠3，
∴∠1＝∠2，
∴AC平分∠DAE；
（2）解：①∵AB为直径，
∴∠AFB＝90°，
而DE⊥AD，
∴BF∥DE，
∴OC⊥BF，
∴＝，
∴∠COE＝∠M，
设⊙O的半径为r，
在Rt△OCE中，cos∠COE＝＝，即＝，解得r＝4，
即⊙O的半径为4；
②连接BF，如图，
在Rt△AFB中，cos∠FAB＝，
∴AF＝8×＝
在Rt△OCE中，OE＝5，OC＝4，
∴CE＝3，
∵AB⊥FM，
∴，
∴∠5＝∠4，
∵FB∥DE，
∴∠5＝∠E＝∠4，
∵＝，
∴∠1＝∠2，
∴△AFN∽△AEC，
∴＝，即＝，
∴FN＝．

24．【解答】解：如图，
销售额
数量


x
人员
4.0≤x≤4.9
5.0≤x≤5.9
6.0≤x≤6.9
7.0≤x≤7.9
8.0≤x≤8.9
9.0≤x≤10.0







乙
0
1
3
0
2
4
（1）估计乙业务员能获得奖金的月份有6个；
（2）可以推断出甲业务员的销售业绩好，理由为：甲的销售额的中位数较大，并且甲月销售额在9万元以上的月份多．
故答案为0，1，3，0，2，4；6；甲，甲的销售额的中位数较大，并且甲月销售额在9万元以上的月份多．
25．【解答】解：（1）经测量，当t＝6时，BP＝3.0．
（当t＝6时，CP＝6﹣BC＝3，
∴BC＝CP．
∵∠C＝60°，
∴当t＝6时，△BCP为等边三角形．）
故答案为：3.0．
（2）描点、连线，画出图象，如图1所示．
（3）在曲线部分的最低点时，BP⊥AC，如图2所示．

26．【解答】解：（1）由上述信息可知该函数图象的顶点坐标为：（3，﹣2），
设二次函数的表达式为：y＝a（x﹣3）2﹣2．
∵该函数图象经过点A（1，0），
∴0＝a（x﹣3）2﹣2，
解得a＝
∴二次函数解析式为：y＝（x﹣3）2﹣2．
（2）如图所示：

当m＞0时，直线y＝m与G有一个交点；
当m＝0时，直线y＝m与G有两个交点；
当﹣2＜m＜0时，直线y＝m与G有三个交点；
当m＝﹣2时，直线y＝m与G有两个交点；
当m＜﹣2时，直线y＝m与G有一个交点．
27．【解答】解：（1）EA1＝FC．理由如下：
∵AB＝BC，∴∠A＝∠C，
∵△ABC绕点B顺时针旋转角α得△A1BC1，
∴∠ABE＝∠C1BF，AB＝BC＝A1B＝BC1，
在△ABE和△C1BF中，，
∴△ABE≌△C1BF（ASA），
∴BE＝BF，
∴A1B﹣BE＝BC﹣BF，
即EA1＝FC；

（2）四边形BC1DA是菱形．理由如下：
∵旋转角α＝30°，
∠ABC＝120°，
∴∠ABC1＝∠ABC+α
＝120°+30°＝150°，
∵∠ABC＝120°，AB＝BC，
∴∠A＝∠C＝（180°﹣120°）＝30°，
∴∠ABC1+∠C1＝150°+30°＝180°，
∠ABC1+∠A＝150°+30°＝180°，
∴AB∥C1D，AD∥BC1，
∴四边形BC1DA是平行四边形，
又∵AB＝BC1，
∴四边形BC1DA是菱形；

（3）过点E作EG⊥AB，
∵∠A＝∠ABA1＝30°，
∴AG＝BG＝AB＝1，
在Rt△AEG中，AE＝＝＝，
由（2）知AD＝AB＝2，
∴DE＝AD﹣AE＝2﹣．


28．【解答】（1）解：∵一次函数y＝x+4 与x轴交于点A，与y轴交于点C，
∴C（0，4），A（﹣5，0）．
∵一次函数y＝﹣x+b经过点C，
∴b＝4，
∴一次函数解析式为y＝﹣x+4．

（2）证明：如图1中，连接AP．

在△APB中，∵PG＝GB，AF＝FB，
∴FG＝AP，
在△APH中，∵AE＝EH，PD＝DH，
∴DE＝AP，
∴FG＝DE．

（3）解：如图2中，延长GF交AQ于K，连接PE．

∵GM＝MF，∠PMG＝∠QMF，PM＝MQ，
∴△PGM≌△QFM，
∴QF＝PG＝GB，∴∠FQM＝∠MPG，
∴QF∥PB，
∴四边形FGBQ是平行四边形，
∴BQ＝FG＝DE，BQ∥DE，可得△DEH≌△QBH，
∴EH＝HB＝AE，
∴H（1，0），设GM＝a，则MF＝a，PA＝4a，
∵GK∥AP，PM＝MQ，
∴AK＝KQ，
∴MK＝2a，FK＝a，
∴FM＝FK，∠MFB＝∠AFK，BF＝AF，
∴△AFK≌△BFM，
∴∠FAK＝∠MBF，
∴BM∥AQ，
∴∠BAQ＝∠ABM，
∵∠BAQ+∠BMQ＝∠DEB＝∠PAB，
∴∠ABM+∠BMQ＝∠PAB＝∠PHA，
∴PA＝PH，∵AE＝EH，
∴PE⊥AH，
设AE＝EH＝x，
则EO＝x﹣1，EO＝OA﹣AE＝5﹣x，
∴5﹣x＝x﹣1，
∴x＝3，
∴PE＝EB＝6，EO＝2，
∴P（﹣2，6）．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2020/4/1 13:34:18；用户：初中校园号；邮箱：wjwl@xyh.com；学号：24424282