






初中数学北师大版九年级上册第一章 特殊平行四边形2 矩形的性质与判定精品ppt课件
展开1.理解矩形的概念,知道矩形与平行四边形的区别与联系.(重点)2.会证明矩形的性质,会用矩形的性质解决简单的问 题.(重点、难点)3.掌握直角三角形斜边中线的性质,并会简单的运用. (重点)
有两组对边分别平行的四边形.
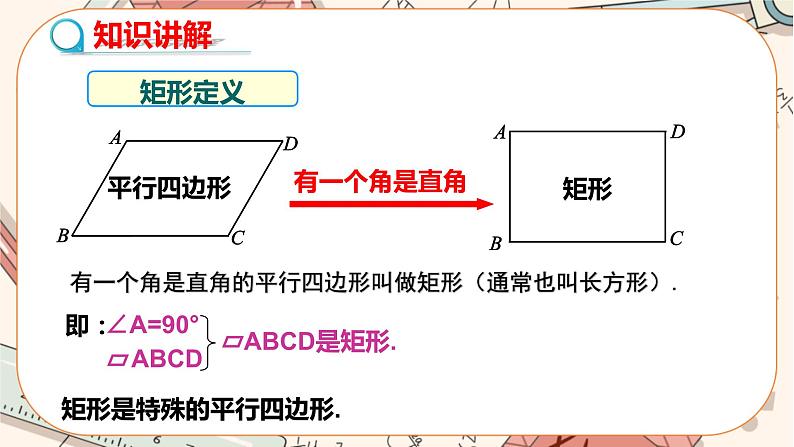
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
矩形是特殊的平行四边形.
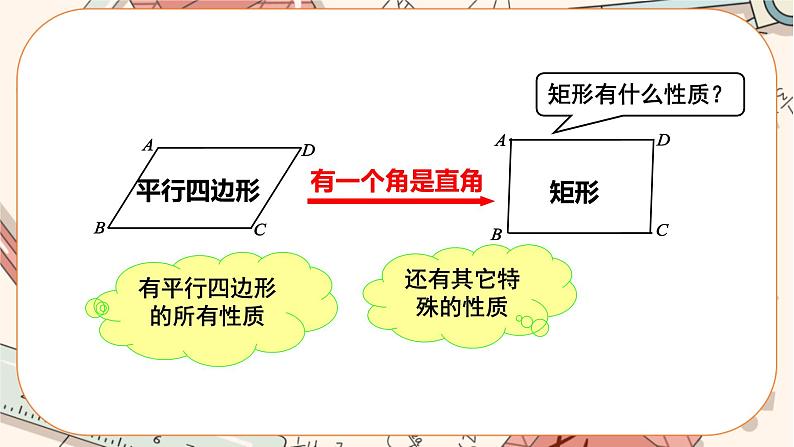
矩形与四边形、平行四边形的关系
有平行四边形的所有性质
矩形的对边平行且相等.
矩形的对角线互相平分.
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
证明:∵四边形ABCD是平行四边形, ∠C=90°,∴∠A=∠C=90° ∠B+∠C=180 °,∴∠B=180-∠C=90°,∴∠D=∠B=90°, 即∠A=∠B=∠C=∠D=90°.
∵四边形ABCD是矩形,∴∠A=∠B=∠C=∠D=90°.
证明:在矩形ABCD中,
∵∠ABC = ∠DCB = 90°,
又∵AB = DC , BC = CB,
∴△ABC≌△DCB(SAS),
∵四边形ABCD是矩形,∴AC=BD.
矩形是轴对称图形,也是中心对称图形.
如图:矩形ABCD的对角线AC与BD交于点O,那么BO是Rt△ABC中一条怎样的特殊线段?它与AC有什么大小关系呢?由此你能得到怎样的结论呢?
提示:大家可以通过测量初步猜测
直角三角形斜边上的中线等于斜边的一半.
直角三角形斜边上的中线的性质
证明:延长BO至D,使OD=BO, 连结AD、DC.
∵AO=OC, BO=OD,∴四边形ABCD是平行四边形.
∵∠ABC=90°,
∵△ABC为直角三角形,BO为AC的中线,
∠DAB=∠ABC=∠BCD=∠CDA=90° ∠AOB=∠DOC ∠AOD=∠BOC∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
△OAB △ OBC △OCD △OAD
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB△OAB≌△OCD △OAD≌△OCB
证明:∵ 四边形ABCD是矩形,∴ ∠B=90°,且AD∥BC,∴ ∠1=∠2.∵ DF⊥AE,∴∠AFD=90°∴∠B=∠AFD.在△ABE和△DFA中, ∠1=∠2, ∠B=∠AFD , AD =AE,∴△ABE≌△DFA(AAS),∴AF=BE,∴EF=EC.
1. 填空:(1)矩形的定义中有两个条件:一是__________ ,二是_______________ .(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为________、________ 、 ______ 、 _______ 。
(3)已知矩形的一条对角线长为10 cm,两条对角线的一个交角为120°,则矩形的边长分别为______ cm,______ cm, ______ cm,_______ cm.
2.下列说法错误的是( )A. 矩形的对角线互相平分。 B. 矩形的对角线相等。C. 有一个角是直角的四边形是矩形。 D. 有一个角是直角的平行四边形叫做矩形。
[答案]公平,因为OA=OC=OB=OD
5.如图,已知BD,CE是△ABC不同边上的高,点G,F分别是BC,DE的中点,试说明GF⊥DE.
解:连接EG,DG.∵BD,CE是△ABC的高,∴∠BDC=∠BEC=90°.∵点G是BC的中点,∴EG=2(1)BC,DG=2(1)BC.∴EG=DG.又∵点F是DE的中点,∴GF⊥DE.
分析:本题的已知条件中已经有直角三角形,有斜边上的中点,由此可联想到应用“直角三角形斜边上的中线等于斜边的一半”这一定理.
矩形的定义:有一个角是直角的平行四边形.
具有平行四边形的一切特征.
直角三角形的一个性质:
北师大版九年级上册2 矩形的性质与判定精品课件ppt: 这是一份北师大版九年级上册2 矩形的性质与判定精品课件ppt,文件包含12矩形的性质与判定第1课时教学课件pptx、第一章特殊平行四边形12矩形的性质与判定第1课时教案内含练习docx等2份课件配套教学资源,其中PPT共33页, 欢迎下载使用。
初中数学北师大版九年级上册第一章 特殊平行四边形2 矩形的性质与判定授课课件ppt: 这是一份初中数学北师大版九年级上册第一章 特殊平行四边形2 矩形的性质与判定授课课件ppt,共42页。PPT课件主要包含了矩形的特殊性质,∴ACBD,求证ACBD,几何语言,ACBD,它的对称轴有几条,探索矩形的对称性,矩形的判定方法,方法总结,跟踪训练等内容,欢迎下载使用。
初中数学北师大版九年级上册第五章 投影与视图2 视图评优课ppt课件: 这是一份初中数学北师大版九年级上册第五章 投影与视图2 视图评优课ppt课件,文件包含52视图第1课时简单几何体的三种视图教学课件pptx、第五章投影与视图52视图第1课时教案内含练习docx等2份课件配套教学资源,其中PPT共21页, 欢迎下载使用。













