数学九年级上册第二章 一元二次方程4 用因式分解法求解一元二次方程优质ppt课件

这是一份数学九年级上册第二章 一元二次方程4 用因式分解法求解一元二次方程优质ppt课件，文件包含24用因式分解法求解一元二次方程教学课件pptx、第二章一元二次方程24用因式分解法求解一元二次方程教案内含练习docx等2份课件配套教学资源，其中PPT共23页， 欢迎下载使用。

理解用因式分解法解方程的依据.
会用因式分解法解一些特殊的一元二次方程.（重点）
会根据方程的特点选用恰当的方法解一元二次方程.（难点）
(2)因式分解有哪些方法？
2. 说出方程(x+3)(x－5)=0的解。
1. (1)什么是因式分解？
把一个多项式分解成几个整式乘积的形式叫做因式分解.
★ 因式分解法解一元二次方程
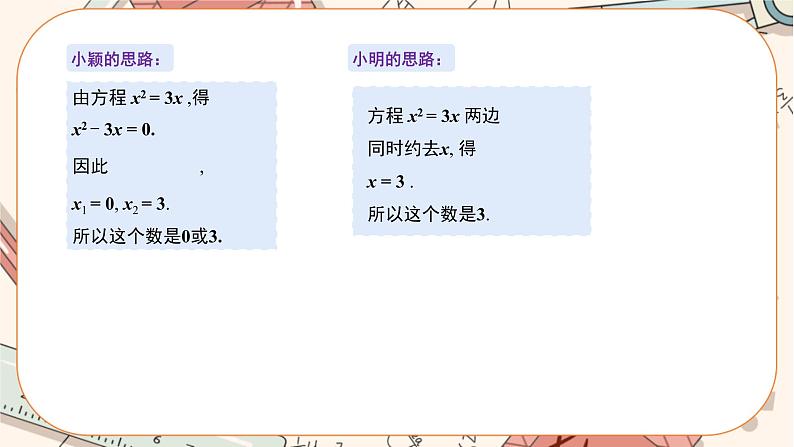
问题：一个数的平方与这个数的3倍有可能相等吗？如果相等,这个数是几？你是怎样求出来的？小颖、小明、小亮都设这个数为x.根据题意,可得方程 x2 = 3x.
由方程 x2 = 3x ,得x2 - 3x = 0.因此 , x1 = 0, x2 = 3.所以这个数是0或3.
方程 x2 = 3x 两边 同时约去x, 得 x = 3 . 所以这个数是3.
两个因式乘积为 0，说明什么？
降次，化为两个一次方程
（解两个一次方程，得出原方程的根）
这种解法是不是很简单？
x2 -3x =0 ①
x(x-3) =0 ②
由方程 x2 = 3x ,得
x1 = 0 , x2 = 3
通过因式分解使一元二次方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解一元二次方程的方法叫做因式分解法.
1.移项：将方程的右边化为0;
2.化积：将方程的左边因式分解为两个一次式的乘积;
3.转化：方程转化为两个一元一次方程;
4.求解：解两个一元一次方程，写出方程两个解.
简记口诀：右化零 左分解两因式 各求解
用因式分解法解下列方程
x2－2x+1 = 0.
( x－1 )( x－1 ) = 0.
( 2x + 11 )( 2x－ 11 ) = 0.
有 2x + 11 = 0 或 2x － 11= 0，
解：把方程的左边进行因式分解，得
几种常见的用因式分解法求解的方程
（1）形如x2 +bx ＝ 0 的一元二次方程，将左边运用提公因式法因式分解为x（x+b）＝ 0，则x ＝ 0 或x+b ＝ 0，即x1= 0， x2 ＝ -b.
（2）形如x2 - a2 ＝ 0 的一元二次方程，将左边用平方差公式因式分解为（x+a）（x-a）＝ 0，则x+a ＝ 0 或x-a ＝ 0，即x1 ＝ -a， x2 ＝ a.
（3）形如x2 ±2ax+ a2 ＝ 0 的一元二次方程，将左边用完全平方公式因式分解为（x± a ）2＝ 0，则① x+a ＝ 0，即x1 ＝ x2 ＝ -a. ② x-a ＝ 0，即x1 ＝ x2 ＝ a.
（4）形如x2 +（a+b）x+ab ＝ 0 的一元二次方程，将其左边因式分解， 则方程化为（x+a）（x+b）＝ 0，所以x+a ＝ 0 或x+b ＝ 0，即x1 ＝ -a， x2 ＝ -b.
★ 选择适当的方法解一元二次方程
用适当的方法解下列方程：
（1）2（x-1）2-18 ＝ 0 ；
分析：出现了（x-1）2，并且一次项为0，考虑用直接开平方法.
解：整理，得（x-1）2＝ 9. 开平方，得x-1 ＝ ±3， 即x-1 ＝ 3 或x-1 ＝ -3， ∴ x1＝4，x2＝-2.
（2）x2+4x-1 ＝ 0 ；
分析：出现了x2 +4x，接近完全平方式的结构特点，考虑用配方法.
（3）9（x+1）2＝（2x-5）2 ；
分析：移项易发现符合平方差公式，考虑用因式分解法.
解：∵ a ＝ 9，b ＝ -12，c ＝ -1， ∴ Δ ＝ b 2-4 a c ＝（-12）2-4×9×（-1）＝ 144+36 ＝ 180>0，
（4）9x2-12x-1 ＝ 0.
分析：方程的结构没有明显特殊性，考虑公式法.
x2 + px + q = 0 （p2 - 4q ≥0）
(x+m)2＝n（n ≥ 0）
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x + m) （x + n）＝0
一元二次方程的解法及适用类型
1.一般地，当一元二次方程一次项系数为0时（ax2+c=0）， 应选用直接开平方法；2.若常数项为0（ ax2+bx=0），应选用因式分解法；3.若一次项系数和常数项都不为0 (ax2+bx+c=0），先化为一般式，看一边的整式是否容易因式分解，若容易，宜选用因式分解法，不然选用公式法；4.当二次项系数是1，且一次项系数是偶数时，用配方法也较简单.
1.下列一元二次方程最适合用因式分解法来解的是( )A．(x－2)(x＋5)＝2 B．(x－2)2＝ x 2－4C． x 2＋5 x －2＝0 D．12(2－ x)2＝3
2．一元二次方程x(x －3)＋3－ x ＝0的根是( )A．1 B．3 C．1和3 D．1和2
3．已知等腰三角形的腰和底的长分别是一元二次方程x 2－4 x ＋3＝0的根，则该三角形的周长可以是( )A．5 B ．7 C．5或7 D．10
6．若正数a是一元二次方程x 2－5x＋m＝0的一个根，－a是一元二次方程x2＋5x－m＝0的一个根，则a的值是 ．
4．方程x 2＝| x |的根是 ．
5．如果x 2－ x －1＝(x ＋1)0，那么x的值为 ．
7．用因式分解法解下列方程：(1)2(x －3)2＝x2－9；
(2)(3x＋2)2－4x2＝0；
(3)5x(2x－3)＝10x－15. 
解：2(x－3)2＝(x＋3)(x－3)，(x－3)[2(x－3)－(x＋3)]＝0.解得x1＝3，x2＝9.
8．已知三角形的两边长分别为3和7，第三边长是方程x(x－7)－10(x－7)＝0的一个根，求这个三角形的周长．
解：解方程x(x－7)－10(x－7)＝0，得x1＝7，x2＝10.当x＝10时，3＋7＝10，∴x2＝10不合题意，舍去．∴这个三角形的周长为3＋7＋7＝17.
简记口诀：右化零 左分解两因式 各求解
如果a ·b=0，那么a=0或b=0
将方程左边因式分解，右边=0
因式分解的方法有ma+mb+mc=m(a+b+c);a2 ±2ab+b2=(a ±b)2；a2 -b2=(a +b)(a -b)