




初中数学湘教版八年级上册2.2 命题与证明教学ppt课件
展开1.知道证明的必要性,掌握证明的基本步骤和书写 格式;(重点)2.掌握反证法证明的基本步骤和格式;(难点)
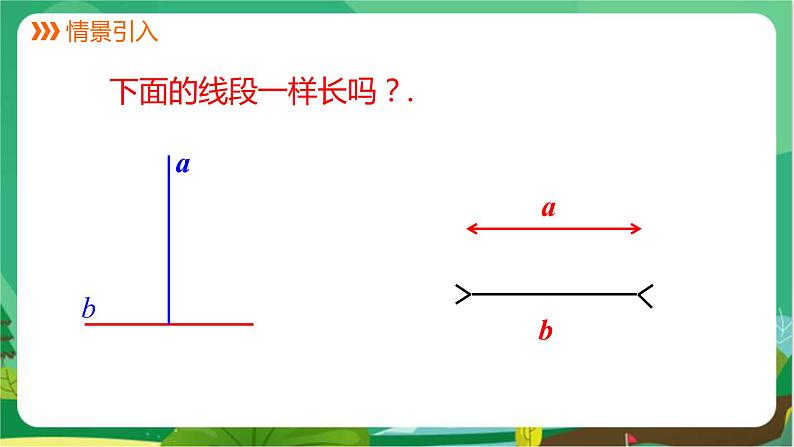
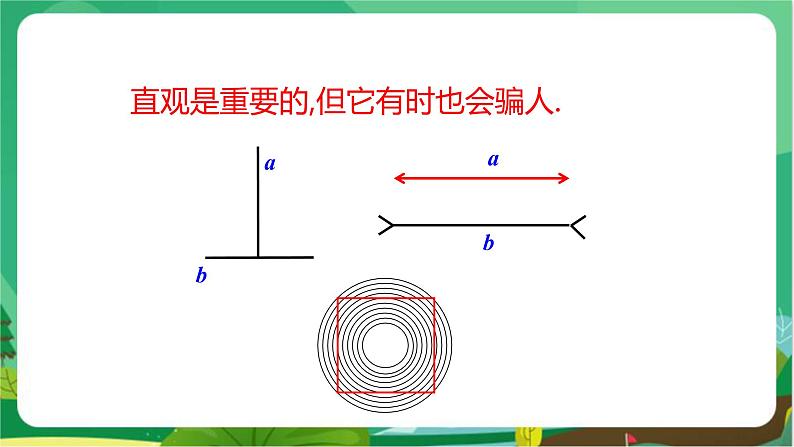
下面的线段一样长吗?.
下面的两个正方形一样吗?.
直观是重要的,但它有时也会骗人.
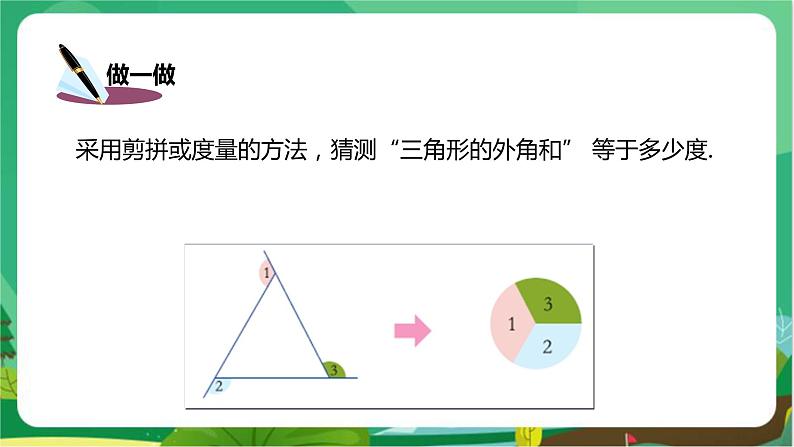
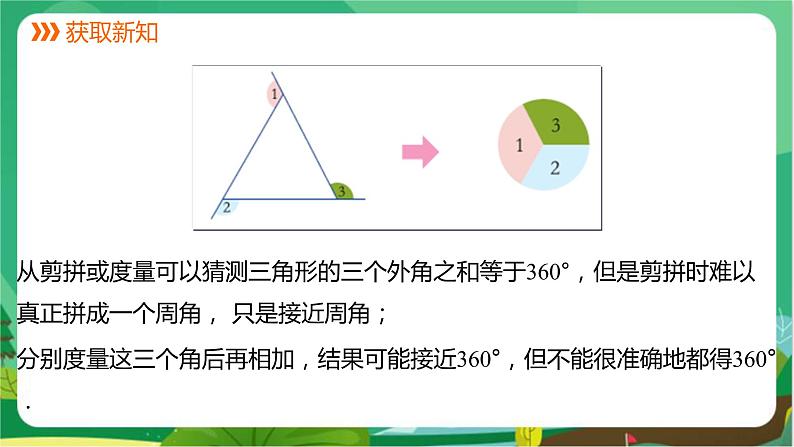
采用剪拼或度量的方法,猜测“三角形的外角和” 等于多少度.
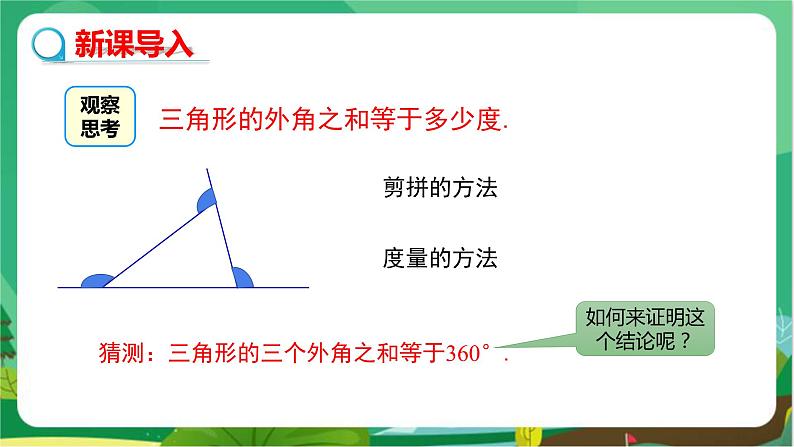
三角形的外角之和等于多少度.
猜测:三角形的三个外角之和等于360°.
如何来证明这个结论呢?
从剪拼或度量可以猜测三角形的三个外角之和等于360°,但是剪拼时难以真正拼成一个周角, 只是接近周角;
分别度量这三个角后再相加,结果可能接近360°,但不能很准确地都得360°.
另外,由于不同形状的三角形有无数个,我们也不可能用剪拼或度量的方法来一一验证,因此,我们只能猜测任何一个三角形的外角和都为360°.
此时猜测出的命题仅仅是一种猜想, 未必都是真命题.要确定这个命题是真命题,还需要通过推理的方法加以证明.
已知:如图,∠BAF,∠CBD和∠ACE分别是△ABC的三个外角.
求证:∠BAF+∠CBD+∠ACE=360°.
∵ ∠BAF=∠2+∠3,
∴∠BAF+∠CBD+∠ACE=2(∠1+∠2+∠3).
∠CBD=∠1+∠3,
∠ACE=∠1+∠2,
∵∠1+∠2+∠3=180°(三角形内角和定理),
∴ ∠BAF+∠CBD+∠ACE =2×180°=360°.
证明与图形有关的命题时,一般有以下步骤:
(1)根据题意,画出图形。
(2)结合图形,写出已知求证
(3)写出证明过程,并且步步有依据。
经过刚才三站的“证明”之旅,你能说出完整的几何命题证明需要哪几个步骤吗?
从一个命题的条件出发,通过讲道理(推理),得出它的结论成立,从而判断该命题为真,这个过程叫做证明 。
( 定义)(定理)(基本事实)
例1 已知:如图,在△ABC中,∠B=∠C,点D在线段BA 的延长线上,射线AE平分∠DAC.
证明:∵∠DAC =∠B +∠C(三角形外角定理),
∴ ∠DAC=2∠B(等式的性质).
又∵AE平分∠DAC(已知),
∴∠DAC=2∠DAE(角平分线的定义)
∴∠DAE=∠B(等量代换).
∴AE∥BC(同位角相等,两直线平行)
例2 已知:∠A,∠B,∠C是△ABC的内角.
求证:∠A,∠B,∠C中至少有一个角大于或等于60°.
解析:这个命题的结论是“至少有一个”,也就是说可能出现“有一个” “有两个” “有三个”这三种情况. 如果直接来证明,将很繁琐,因此,我们将从另外一个角度来证明.
证明:假设∠A,∠B,∠C 中没有一个角大于或等于60°,
即∠A<60°,∠B<60°,∠C<60°,
则∠A+∠B+∠C<180°.
这与“三角形的内角和等于180°”矛盾,
因此,∠A, ∠B, ∠C中至少有一个角大于或等于60°.
像这样,先假设命题不成立,然后利用命题的条件或有关的结论,通过推理导出矛盾,从而得出假设不成立,即所证明的命题正确,这种证明方法称为反证法.
反证法是一种间接证明的方法,其基本的思路可归结为“否定结论,导出矛盾,肯定结论”.
应用反证法的情形:(1) 直接证明困难;(2) 直接证明需分成很多情况进行讨论;(3) 结论为“至少”、“至多”、“有无穷多个” 的一类命题; (4) 结论为 “唯一”类命题.
用反正法证明时,导出矛盾的几种可能:
(1)与原命题的条件矛盾;
(3)与定义、公理、定理、性质矛盾;
(4)与客观事实矛盾.
1. 已知:如图,AB与CD 相交于点E. 求证:∠A+∠C=∠B+∠D.
证明: ∵ AB与CD 相交于点E ,
∴ ∠AEC=∠BED (对顶角相等),
又 ∵∠A+∠C +∠AEC =∠B+∠D +∠BED =180°(三角形内角和等于180°),
证明:因为∠AGB=∠2(对顶角相等), ∠1=∠2(已知),所以 ∠1=∠AGB(等量代换),所以CE∥BF(同位角相等,两直线平行).所以∠C=∠BFD(两直线平行,同位角相等).因为∠B=∠C,所以∠B=∠BFD(等量代换),所以AB∥CD(内错角相等,两直线平行),所以∠A=∠D(两直线平行,内错角相等).
4.求证:△ABC中不能有两个钝角.
证明:假设△ABC中能有两个钝角,即∠A<90°,∠B>90°,∠C>90°, 所以∠A+∠B+∠C>180°,与三角形的内角和为180°矛盾, 所以假设不成立,因此原命题正确,即△ABC中不能有两个钝角.
1. 在括号内填上理由.
已知:如图,∠A+∠B= 180°.求证:∠C+∠D= 180°.证明:∵∠A+∠B= 180°(已知), ∴ AD∥BC( ). ∴ ∠C+∠D= 180° ( ).
同旁内角互补,两直线平行
两直线平行,同旁内角互补
2. 已知:如图,直线AB,CD被直线MN所截, ∠1=∠2. 求证:∠2=∠3,∠3+∠4=180°.
证明: ∵ ∠1=∠2,
∴ ∠2 =∠3(两直线平行,内错角相等)
∠3+∠4=180°(两直线平行, 同旁内角互补).
∴ AB∥CD(同位角相等,两直线平行)
3. 已知:如图,AB与CD 相交于点E. 求证:∠A+∠C=∠B+∠D.
又 ∠A+∠C +∠AEC =∠B+∠D +∠BED =180°(三角形内角和等于180°),
1如图,∠1+∠2=180°,若∠3=50°,则∠4= 50° .
2如图,已知AD∥BC,∠1=∠2,则下列结论不成立的是( C )
3如图,DH∥EG∥BC,DC∥EF,与∠1相等的角有( D )
(1)如果∠1=∠2,那么 AD ∥ BC ;( 内错角相等,两直线平行 )
4根据图形填空,并填上推理的依据.
(2)如果∠3=∠4,那么 AB ∥ CD ;( 内错角相等,两直线平行 )
(3)如果∠5=∠ABC,那么 AD ∥ BC ;
( 同位角相等,两直线平行 )
(4)如果∠DAB+∠ADC=180°,那么 AB ∥ CD .( 同旁内角互补,两直线平行 )
同位角相等,两直线平行
同旁内角互补,两直线平行
5如图,下列推理及所给出的理由正确的是( C )
①因为∠B=∠BEF,所以AB∥EF;
②因为∠B=∠CDE,所以AB∥CD;
③因为∠DCE+∠AEF=180°,所以AB∥EF;
6如图,给出下面的推理:
④因为∠A+∠AEF=180°,所以AB∥EF.
其中正确的推理是( B )
7如图,AB∥CD,EF为直线,∠1=63°,∠2=27°,求证:EF⊥CD.
证明:因为AB∥CD,(已知)所以∠1=∠3.(两直线平行,同位角相等)又因为∠2=27°,∠1=63°,(已知)所以∠EFC=∠2+∠3=27°+63°=90°.所以EF⊥CD.(垂直的定义)
8如图,AC∥DF,AB∥EF,点D、E分别在AB、AC上,求证:∠1=∠2.
证明:∵AB∥EF,∴∠A=∠2.∵AC∥DF,∴∠1=∠A,∴∠1=∠2.
9如图,根据已知条件,直线AB与直线CD平行吗?说说你的理由.
解:直线AB与直线CD平行.
理由:∵∠AGH=110°,∴∠BGH=180°-110°=70°(邻补角定义).而∠DHF=70°,即∠BGH=∠DHF,∴AB∥CD(同位角相等,两直线平行).(证明方法不唯一,正确即可)
10如图,有三个论断:①∠1=∠2;②∠B=∠D;③∠A=∠C,请从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
解:已知∠B=∠D,∠A=∠C.
证明:∵∠A=∠C,∴AB∥CD,∴∠B=∠BFC.∵∠B=∠D,∴∠BFC=∠D.∴DE∥BF.∴∠DMN=∠BNM.∵∠1=∠DMN,∠2=∠BNM,∴∠1=∠2.
(画图)写出已知、求证
八年级上册2.2 命题与证明教学课件ppt: 这是一份八年级上册2.2 命题与证明教学课件ppt,文件包含教学课件八上·湘教·22命题与证明第2课时真假命题与定理pptx、222docx等2份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
初中数学湘教版八年级上册2.2 命题与证明教学课件ppt: 这是一份初中数学湘教版八年级上册2.2 命题与证明教学课件ppt,文件包含教学课件八上·湘教·22命题与证明第1课时定义与命题pptx、221docx等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。
湘教版八年级上册2.2 命题与证明评课ppt课件: 这是一份湘教版八年级上册2.2 命题与证明评课ppt课件,共13页。PPT课件主要包含了不是命题,是命题,绝对值等内容,欢迎下载使用。













