







数学九年级上册23.1 平均数与加权平均数教学ppt课件
展开第二十三章 数据分析
23.1 平均数与加权平均数
第2课时 加权平均数
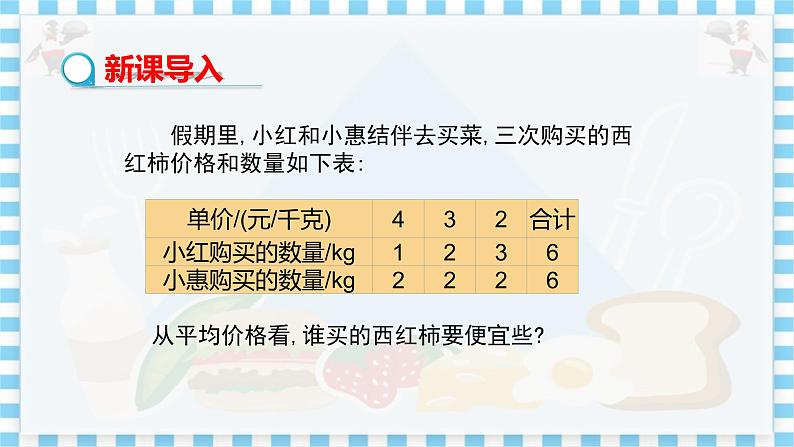
教学目标 1.理解数据的权和加权平均数的概念,体会权的作用. 2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法. 教学重难点 重点:掌握加权平均数的计算方法. 难点:理解数据的权和加权平均数的概念. 教学过程 导入新课 问题:假期里,小红和小惠结伴去买菜,三次购买的西红柿价格和数量如下表:
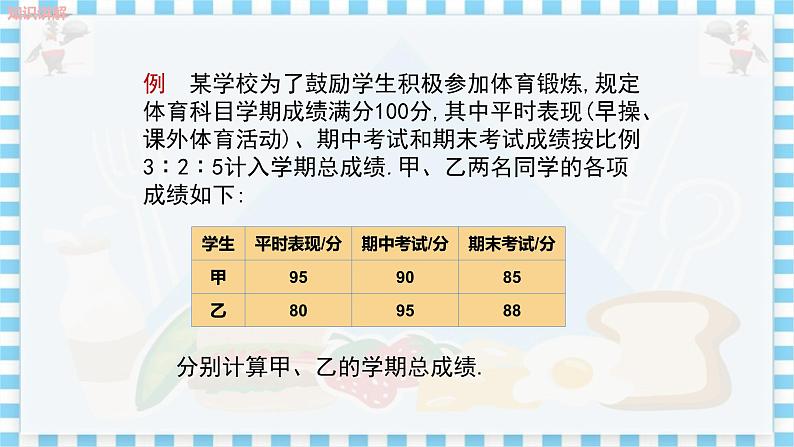
从平均价格看,谁买的西红柿要便宜些? 学生思考如何解决? 思考小亮和小明的下列说法,你认为他俩谁说得对?为什么? 小亮的说法: 每次购买单价相同,购买总量也相同,平均价格应该也一样,都是(4+3+2)÷3=3(元/千克). 小明的说法: 购买的总量虽然相同,但小红花了16元,小慧花了18元,所以平均价格不一样,小红买的西红柿要便宜些. 探究新知 解决上面的问题 小红购买不同单价的西红柿的数量不同,所以平均价格不是三个单价的平均数.实际上,平均价格是总花费金额与购买总量的比,因此 ≈2.67(元/千克), =3(元/千克). 从平均价格看,小红买的西红柿要便宜些. 老师引领学生思考 从上面这个问题你看出了什么?遇到这种情况所求的平均数与算术平均数一样吗? 学生:数据出现的次数不同,即比重不同时,所求的平均数不是算术平均数. 老师给出加权平均数的概念. 加权平均数 已知n个数 x1, x2 ,…,xn,若 w1, w2 ,…, wn为一组正数,则把 叫做 n个数 x1 , x2,…, xn 的加权平均数, w1, w2,…, wn分别叫做这n个数的权重,简称为权. 思考:在前面买西红柿的问题中,加权平均数是多少?哪些数是权? 小红购买的西红柿平均价格约为2.67元/千克,它是数4,3,2的加权平均数,三个数的权分别为1,2,3. 例 某学校为了鼓励学生积极参加体育锻炼,规定体育科目学期成绩满分为100分,其中平时表现(早操、课外体育活动)、期中考试和期末考试成绩按比例3∶2∶5计入学期总成绩.甲、乙两名同学的各项成绩如下:
分别计算甲、乙的学期总成绩. 解:三项成绩按3∶2∶5的比例确定,就是分别用3,2,5作为三项成绩的权,用加权平均数作为学期总成绩. 甲的学期总成绩为=89(分), 乙的学期总成绩为=87(分). 思考: (1)分配的“权”不同,甲、乙二人的总成绩是否会发生变化? 回答:分配的“权”不同,甲、乙二人的总成绩会发生变化. (2)算术平均数和加权平均数的区别和联系是什么? 回答:算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数. 练习:某电视节目主持人大赛要进行专业素质、综合素质、外语水平和临场应变能力四项测试,各项测试均采用10分制,两名选手的各项测试成绩如下表所示:
(1)如果按四项测试成绩的算术平均数排名次,名次是怎样的? (2)如果规定按专业素质、综合素质、外语水平和临场应变能力四项测试的成绩各占60%,20%,10%,10%计算总成绩,名次有什么变化? 解:(1)甲、乙各项成绩的算术平均数分别为: =8.45(分), =8.65(分). 比较算术平均数,乙排名第一,甲排名第二. (2)甲、乙的加权平均成绩分别为: =9.0×60%+8.5×20%+7.5×10%+8.8×10%=8.73(分), =8.0×60%+9.2×20%+8.4×10%+9.0×10%=8.38(分). 比较加权平均数,甲排名第一,乙排名第二. 总结:权主要有三种表现形式:百分比,比例,数据出现的次数. 老师带领总结加权平均数的意义 加权平均数不仅与每个数据的大小有关,还受每个数据的权的影响. 数据的“权”反映数据的“重要程度”. 权越大,该数据所占的比重越大;反之,权越小,该数据所占的比重越小. 注意:(1)一组数据的平均数是唯一的. (2)平均数的单位要与原数据的单位一致. (3)一组数据的平均数不一定是这组数据中的数. 课堂练习 1.某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:
(1)如果根据三项测试的平均成绩决定录用人选,那么谁将被录用? (2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4∶3∶1的比例确定各人测试成绩,此时谁将被录用? 2.某校规定学生的体育成绩由三部分组成:早锻炼及体育课外活动表现占成绩的20%,体育理论测试占30%,体育技能测试占50%,小颖的上述三项成绩依次是92分、80分、84分,则小颖这学期的体育成绩是多少? 参考答案 1.解:(1)A的平均成绩为(72+50+88)÷3=70(分). B的平均成绩为(85+74+45)÷3=68(分). C的平均成绩为(67+70+67)÷3=68(分). 由于70>68,故A将被录用. (2)A的测试成绩为(72×4+50×3+88×1)÷(4+3+1)=65.75(分). B的测试成绩为(85×4+74×3+45×1)÷(4+3+1)=75.875(分). C的测试成绩为(67×4+70×3+67×1)÷(4+3+1)=68.125(分). 因此候选人B将被录用. 2.解:小颖这学期的体育成绩是92×20%+80×30%+84×50%=84.4(分). 答:小颖这学期的体育成绩是84.4分. 课堂小结 加权平均数 已知n个数 x1, x2 ,…,xn,若 w1, w2 ,…, wn为一组正数,则把叫做 n个数 x1 , x2,…, xn 的加权平均数, w1, w2,…, wn分别叫做这n个数的权重,简称为权. 布置作业 教材第8页习题A组. 板书设计 23.1 平均数与加权平均数 第2课时 加权平均数 加权平均数 已知n个数 x1, x2 ,…,xn,若 w1, w2 ,…, wn为一组正数,则把叫做 n个数 x1 , x2,…, xn 的加权平均数, w1, w2,…, wn分别叫做这n个数的权重,简称为权. 加权平均数的意义
| 教学反思
教学反思
教学反思
教学反思
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
初中数学第23章 数据分析23.1 平均数与加权平均数教学课件ppt: 这是一份初中数学第23章 数据分析23.1 平均数与加权平均数教学课件ppt,文件包含教学课件九上·河北教育版·231平均数与加权平均数第3课时用样本平均数估计总体平均数-副本pptx、2313docx等2份课件配套教学资源,其中PPT共13页, 欢迎下载使用。
初中数学冀教版九年级上册23.1 平均数与加权平均数教学课件ppt: 这是一份初中数学冀教版九年级上册23.1 平均数与加权平均数教学课件ppt,文件包含教学课件九上·河北教育版·231平均数与加权平均数第1课时平均数pptx、2311docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
2021学年23.1 平均数与加权平均数多媒体教学课件ppt: 这是一份2021学年23.1 平均数与加权平均数多媒体教学课件ppt,共25页。PPT课件主要包含了情境引入,学习目标,平均数,先和后分,移多补少,平均水平,平均数与加权平均数,合作探究,算术平均数,典例解析等内容,欢迎下载使用。













