初中数学25.1 比例线段教学课件ppt

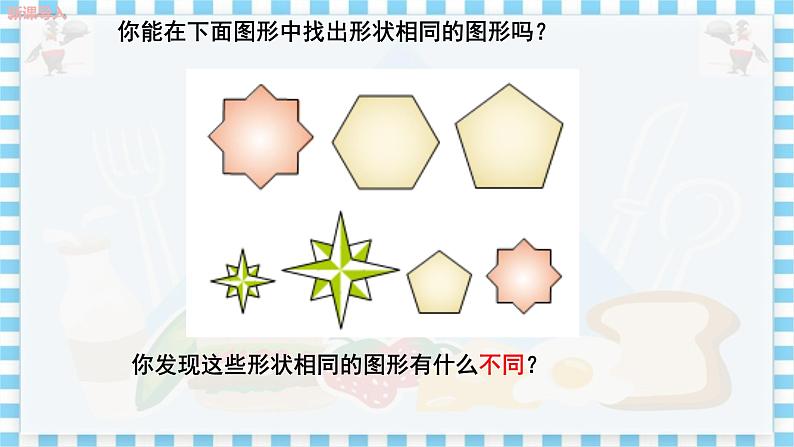
教学目标

1.知道线段的比和比例线段的概念，会求两条线段的比.

2.理解并掌握比例的基本性质及其应用.

3.结合实例了解黄金分割.

教学重难点

重点：理解线段的比与成比例线段的概念及求解.

难点：运用比例的性质解决问题.

教学过程

导入新课

1.通过用幻灯片展示几组形状相同但大小不同的图片，让学生进行对比，引发学生思考.

2.再给出几组形状相同的图形.

你能在下面图形中找出形状相同的图形吗？

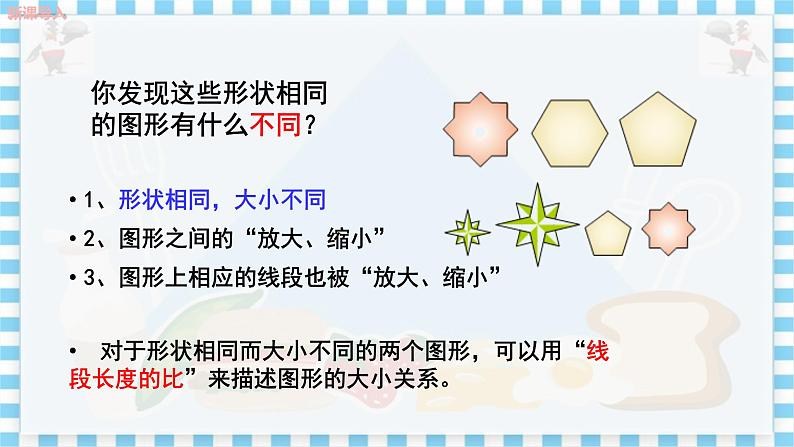
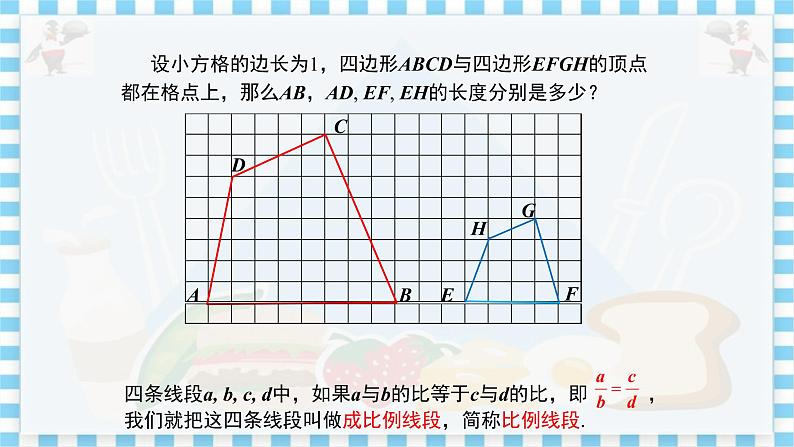
师：对于上面我们给出的几组图形，形状相同的图形有什么不同吗？

生：大小不同.

师：大小不同的两个图形我们应该怎样得到呢？

生：通过图形之间的放大或者缩小得到另一个图形.

师：图形上相应的线段关系又如何呢？

生：放大或缩小的同时图形上相应的线段也被放大或缩小.

师：这样对于形状相同而大小不同的两个图形，我们可以用相应线段长度的比来描述图形的大小关系.

设计意图：通过生活中常见的实物图片和图形，引发学生进行对比和思考，这样能激发学生学习的兴趣，从而开始愉快的一节课.

探究新知

探究点一　线段的比与成比例线段

师：怎样度量线段的长度？怎样比较两条线段的大小？

生：度量线段的长度时要选用同一度量单位，比较线段的大小就是比较线段长度的大小.

师：由此大家能猜想线段的比吗？

生：两条线段的比就是两条线段长度的比.

师：那么我们应怎样定义两条线段的比呢？求比时应注意什么问题呢？

生：如果选用同一个度量单位，量得两条线段AB和CD的长度分别是m和n，我们就把m和n的比叫做线段AB和CD的比.即AB∶CD＝m∶n，或写成.其中，线段AB，CD分别叫做这个线段比的前项和后项. 如果把表示成比值k，那么＝k，或AB＝k·CD.两条线段的比实际上就是两个数的比.

  注意：1.两条线段的比就是其长度的比，它是一个数，它没有单位.比值总是正的.

2.两条线段的比是有顺序的. 

3.两条线段的比与所选的长度单位无关.     

4.求两条线段的比时，如果单位不同，那么必须先化成同一单位，再求它们的比.

  巩固练习

若线段AB＝12 cm，CD＝8 cm，则＝________.

  答案：

设计意图：通过层层问题让学生理解线段的比的概念，这样大大降低了学习难度，学生能较容易地接受新知识.

图1

师：用多媒体展示图1，设小方格的边长为1，四边形ABCD与四边形EFGH的顶点都在格点上.回答下列问题：

（1）求线段AB，AD，EF，EH的长度.

（2）分别计算，，，的值，你发现了什么？

学生独立完成第1小题，然后小组讨论第2小题，让小组代表发表本小组的见解.

学生总结，教师点评：

通过计算得到＝，＝.

师：这样的线段有什么专有名称？

生：这样的线段我们把它叫做成比例线段.

最后教师点评：在四条线段a，b，c，d中，如果a与b的比等于c与d的比，即，我们就把这四条线段叫做成比例线段，简称比例线段.

由此可知AB，EF，AD，EH是成比例线段，AB，AD，EF，EH也是成比例线段.

注意：四条线段成比例与这四条线段的排列顺序有关.

探究点二　比例的基本性质

师：如果线段a，b，c，d成比例，即，那么ad＝bc 吗？

生：由等式的基本性质，在两边同乘以bd，得ad＝bc.

师：反之，如果线段a，b，c，d满足ad＝bc，那么这四条线段成比例吗？

生：成比例.

由教师补充，由等积式得到比例式时要注意a，b，c，d都不等于0.

教师总结：

比例的基本性质：（1）如果，那么ad＝bc；

（2）如果ad＝bc，那么（b，d≠0）.

两内项之积，等于两外项之积.

探究点三　等比性质

师：已知a，b，c，d，e，f 六个数，如果(b＋d＋f≠0)，那么成立吗？

生：成立

师：你是怎么得到的呢？

生：令，

所以a=bk，c=dk，e=fk，

所以.

师：我们把这种方法叫k方法.

如果＝＝…＝(b＋d＋…＋n≠0)，那么.

我们把这条性质叫做比例的等比性质.

注意：在运用等比性质时，前提是分母b＋d＋…＋n≠0.

巩固练习

已知(n＋q0)，则

A.                          B.                        C.                           D.1

答案：B

探究点四　黄金分割

问题：如图2所示，已知线段AB=a，点C在AB上.

图2

当时，线段AC的长是多少?

解：设AC＝x，则BC＝a-x.

∵ ，∴ ，

∴ 建立关于x的方程，

解得.

∵ AC的长为正数，∴ AC＝.

总结：在线段AB上有一点C，如果点C把AB分成的两条线段AC和BC满足，那么称线段AB被点C黄金分割，点C称为线段AB的黄金分割点，称为黄金比. 

每条线段上的黄金分割点都有两个.

新知应用

例1　判断下列线段a，b，c，d是否为成比例线段.

（1）；

（2）.

解：（1）∵

∴ ，

∴ 线段a，b，c，d不是成比例线段.

（2）∵

∴ ，

∴线段a，b，c，d是成比例线段.

例2　根据下列条件，求a∶b的值.

（1）4a=5b；（2）.

解：（1）∵ 4a=5b，∴ .

（2）∵ ，∴ 8a＝7b，∴ .

例3　在△ABC与△DEF中，已知，且△ABC的周长为18，求△DEF的周长.

【问题探索】利用比例的等比性质得出两个三角形的周长比，这样就能求出△DEF的周长.

解：∵，∴ ，

∴ 4（AB+BC+CA）＝3（DE+EF+FD），

即DE+EF+FD＝（AB+BC+CA）.

又∵△ABC的周长为18，即AB+BC+CA＝18，

∴ DE+EF+FD＝（AB+BC+CA）＝24，

∴ △DEF的周长为24.

【总结】比例的等比性质是解决本题的关键，一定要会灵活运用.

课堂练习

1.若两地的实际距离为300 km，图上距离为3 cm，则这张地图的比例尺为(　　)

A.1 000 000：1                 B.10 000 000：1           

C.1：1 000 000                 D.1：10 000 000

2.下列四条线段中，不能成比例的是(　　)

A.a＝3，b＝6，c＝4，d＝8                   

B.a＝1，b＝，c＝，d＝             

C.a＝4，b＝6，c＝5，d＝10                  

D.a＝2，b＝，c＝，d＝

3.（1）已知，那么＝　　　　，＝　　　　.

（2）如果，那么＝　　　　.

（3）如果，那么　　　　.

4.如果求m的值.

5.已知线段a＝0.3 m，b＝60 cm，c＝12 dm.

(1)求线段a与线段b的比；

(2)如果线段a，b，c，d成比例，求线段d的长.

6.已知a，b，c是△ABC的三边，满足且a＋b＋c＝12，请你探索△ABC的形状.

参考答案

1.D　

2.C

3.

4.解：①当x＋y＋z＝0时，

y＋z＝－x，z＋x＝－y，x＋y＝－z，

∴ m为其中任何一个比值，即m＝＝－1.

②当x＋y＋z≠0时，

m＝＝＝2.

∴ m＝2或－1.

5.解：(1)∵ a＝0.3 m＝30 cm，b＝60 cm，

∴ a∶b＝30∶60＝1∶2.

(2)∵线段a，b，c，d成比例，

∴ .

∵ c＝12 dm＝120 cm，

∴ ，∴d＝240 cm.

6.解：设可得a＝3k－4，b＝2k－3，c＝4k－8，

代入a＋b＋c＝12，得9k－15＝12，解得k＝3，

则a＝5，b＝3，c＝4，∴b2＋c2＝a2，即△ABC为直角三角形.

课堂小结

布置作业

习题A组、B组.

板书设计

25.1　比例线段

成比例线段：在四条线段a，b，c，d中，如果a与b的比等于c与d的比，即，我们就把这四条线段叫做成比例线段，简称比例线段.

比例的基本性质：（1）如果，那么ad＝bc；

（2）如果ad＝bc，那么（b，d≠0）.

比例的等比性质：如果＝＝…＝(b＋d＋…＋n≠0)，那么＝.

教学反思

教学反思

教学反思

教学反思

教学反思

教学反思