初中数学冀教版九年级上册26.1 锐角三角函数教学ppt课件

这是一份初中数学冀教版九年级上册26.1 锐角三角函数教学ppt课件，文件包含教学课件九上·河北教育版·261锐角三角函数第1课时正切pptx、2611docx等2份课件配套教学资源，其中PPT共27页， 欢迎下载使用。
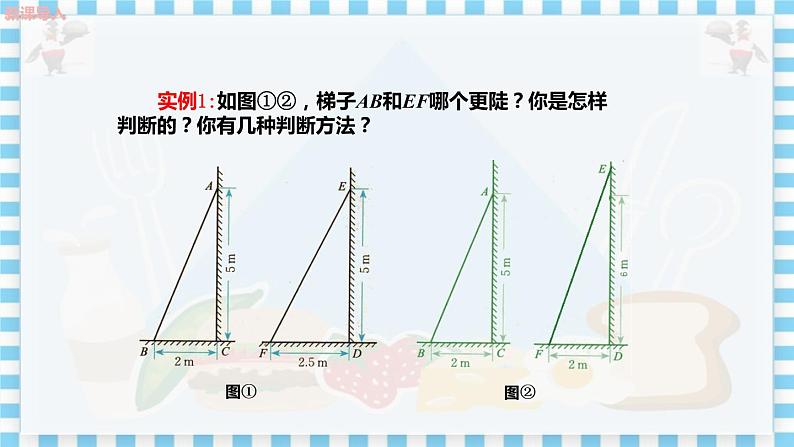
第二十六章　解直角三角形26.1　锐角三角函数第1课时  正切教学目标1.理解正切的意义和与现实生活的联系.2.能够根据直角三角形的边角关系，用正切进行简单的计算.教学重难点重点：理解正切的定义.难点：用正切进行简单的计算.教学过程复习巩固1.直角三角形两锐角、三边之间的关系：如图1，在Rt △ABC中，∠C＝90°.两锐角关系：∠A+∠B＝90°.三边关系：AC 2 + BC 2 ＝AB2.2.相似三角形的性质：相似三角形对应边成比例，对应角相等.导入新课活动1（学生交流，教师点评）【探究】任意画Rt△ABC 和Rt△A′B′C′，使得∠C＝∠C′＝90°，∠A＝∠A′＝α，那么与有什么关系.能解释一下吗？图2教师引出课题： 第二十六章 解直角三角形26.1　锐角三角函数第1课时  正切探究新知探究点一　锐角的正切活动2（学生交流，教师点评）1.如图3所示，在Rt△ABC 和Rt△A′B′C′中，因为∠C＝∠C′＝90°，∠A＝∠A′＝α，所以Rt△ABC∽Rt△A′B′C′，则两个三角形的两组直角边之间有怎样的关系？学生回答：.                        图32.如图4所示，已知∠EAF<90°，BC⊥AF，B'C'⊥AF，垂足分别为C，C'.与具有怎样的关系?  学生回答：＝教师总结：在两个直角三角形中，当一对锐角相等时，这两个直角三角形相似，从而两条对应直角边的比相等，即当∠A(小于90°)确定时，以∠A为锐角的Rt△ABC的两条直角边的比是确定的.这就是说，在Rt△ABC中，当锐角∠A的度数一定时，不管三角形的大小如何，∠A的对边与∠A的邻边的比都是一个固定值.【总结】∠A的正切的定义在Rt△ABC中，∠C＝90°，∠A的对边为a，∠A的邻边为b，斜边为c.∠A的对边与邻边的比叫做∠A的正切，记作tan A，即tan A＝＝.【思考】师生互动(1)∠A的正切tan A表示的是tan 与A的乘积还是一个整体?学生：tan A表示的是一个整体.(2)当∠A的大小变化时，tan A是否变化?学生：tan A随着∠A的大小变化而变化.(3)tan A有单位吗?学生：tan A是一个比值，没有单位.(4)∠B的正切怎么表示?tan A与tan B之间有怎样的关系?学生：(5)要求一个锐角的正切值，我们需要知道直角三角形中的哪些边?学生：需要知道这个锐角的对边和邻边.(6)若知道直角三角形的斜边和一直角边，你能求一个锐角的正切值吗?学生：根据勾股定理求出另一直角边，再根据正切定义求解.【注意】1.正切是一个比值，没有单位.2.正切值只与角的大小有关，与三角形的大小无关.3.tan A是一个整体符号，不能写成tan A，tan A不表示“tan”乘以“A ”.4.当用三个字母表示角时，角的符号“∠”不能省略，如tan∠ABC.5.tan2A表示(tan A)2，而不能写成tan A2.新知应用例1　在Rt△ABC中，∠C=90°.(1)如图6(1)所示，∠A=30°，求tan A，tan B的值.(2)如图6(2)所示，∠A=45°，求tan A的值.         （1）                    （2）图6解：(1)在Rt△ABC中，∵ ∠A=30°，∴ ∠B＝60°，且a＝.∴ b＝.∴ ，.(2)在Rt△ABC中，∵∠A=45°，∴a=b.∴tan A=tan 45°＝.这样，就得到 tan 30°＝，tan 45°=1，tan 60°＝.探究点二  正切的应用【问题】　如图7（1）（2）所示，梯子AB和EF哪个更陡？你是怎样判断的？        （1）                         （2）图7师生互动：学生回答，教师点评.学生：梯子的铅直高度与其水平距离的比相同时，梯子就一样陡.若比不同，比值大的梯子更陡.【归纳总结】1.当梯子与地面所成的角为锐角A时，tan A＝，tan A的值越大，梯子越陡.因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.2.当倾斜角确定时，其对边与邻边之比随之确定，这一比值只与倾斜角的大小有关，而与物体的长度无关.新知应用例2  如图8表示甲、乙两个自动扶梯，哪一个自动扶梯比较陡?     图8解：甲梯中，.乙梯中，.∵ ，∴ 甲梯更陡.课堂练习1.如图9所示，在Rt△ABC中，∠C=90°，三边分别为a，b，c，则tan A等于(　　)图9A.　　　　　　　B.　　　　　　　C.　　　　　　　D.2.把△ABC三边的长度都扩大为原来的3倍，则锐角A的正切值 (　　)A.不变  B.缩小为原来的C.扩大为原来的3倍 D.不能确定3.在Rt△ABC中，∠C＝90°，若斜边AB是直角边BC的3倍，则tan B的值是(　　)A.　　　　　　　B.3　　　　　　　　C.　　　　　　D.4.如图10，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是(　    )A.2                                  B.    C.                                D.5.已知Rt△ABC中，∠C=90°，tan A=，BC=12，则AC等于　　　　. 6.如图11，在Rt△ABC中，∠C＝90°，，则tan A＝　　　　.              　　　　           图11　　　　　   　　   　　图12　　　　7.如图12，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB，垂足为D，则tan∠BCD＝____.8.如图13所示，在Rt△ABC中，∠C=90°.(1)若tan A=，BC=9，求AB的长;(2)若tan B=，AC=16，求AB的长.参考答案1.B　 2.A   3.D   4. D5.9　解析：根据正切定义可得＝，所以AC＝9.故填9.6.　解析：由正切定义可知，因为，可设AB＝17a，BC＝15a，从而可用勾股定理得出第三边AC＝8a，再用正切的定义求解得.7.　解析：根据题意得∠BCD＝∠CAB，所以tan∠BCD＝tan∠CAB＝.8.解：（1）∵tan A＝，又BC=9，∴AC=12.由勾股定理可得AB＝＝15.∴AB的长为15.（2）∵ ，AC＝16，∴  BC＝12.由勾股定理可得AB＝＝20.∴ AB的长为20.课堂小结(学生总结，老师点评)锐角∠A的正切如图14，在Rt△ABC中，如果锐角A确定，那么∠A的对边与邻边的比便随之确定，这个比叫做 ∠A的正切，记作tan A，tan A＝ ＝.【注意】tan A的大小只与∠A的大小有关，而与直角三角形的边长无关.布置作业教材第106页练习题A组第1，2题.B组第1，2题板书设计26.1　锐角三角函数第1课时  正切【探究】　　　　　　正切：在Rt△ABC中，∠C=90°.           　  例1 tan A＝ ＝.                例2 教学反思                   教学反思                       教学反思                       教学反思                       教学反思