冀教版数学九上 28.3 圆心角和圆周角（第3课时） 教学课件+教案

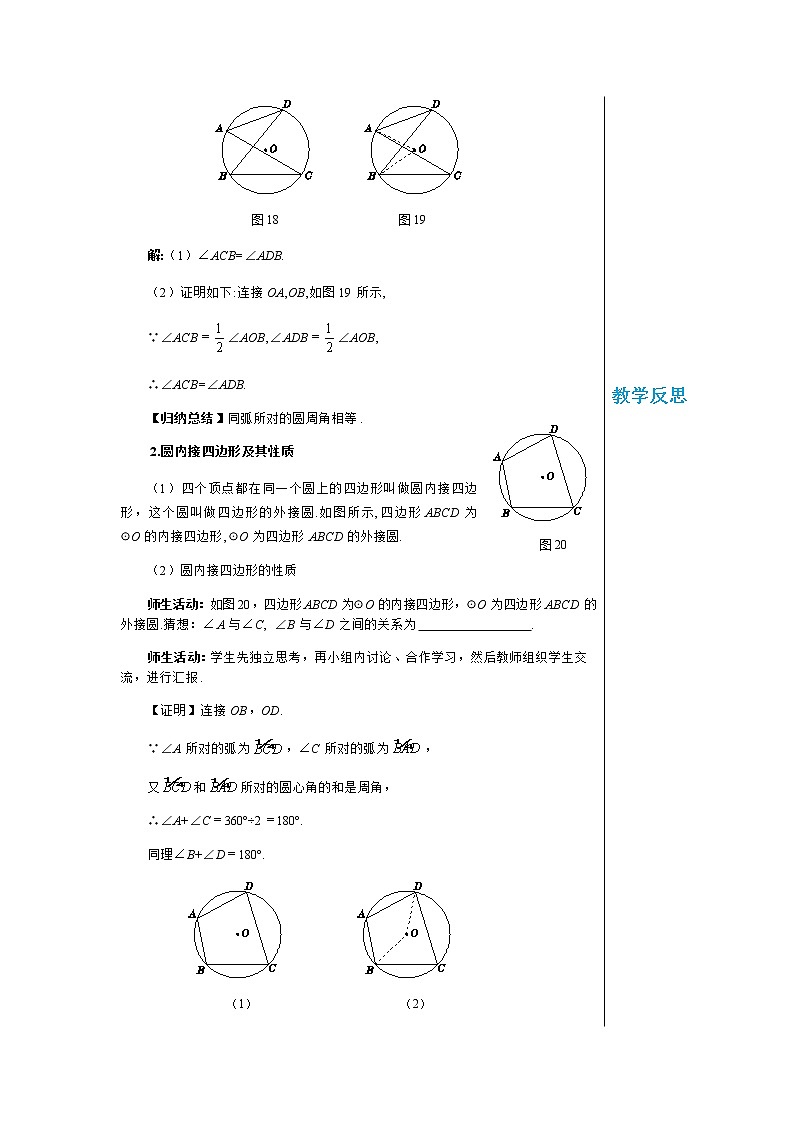
教学目标

1.掌握圆周角定理的另一个推论.

2.理解圆内接四边形和四边形的外接圆的概念.

3.掌握圆内接四边形的性质,并会用此性质进行有关的计算和证明.

教学重难点

重点：同弧所对的圆周角相等、圆内接多边形的概念及圆内接四边形的性质.

难点：同弧所对的圆周角相等、圆内接四边形性质的探究过程及应用.

教学过程

复习提问

1.什么是圆心角、圆周角?

2.同弧所对的圆周角和圆心角有什么关系?

3.直径所对的圆周角是多少度?90°的圆周角所对的弦是直径吗?

设计意图　通过复习圆周角定理及推论,巩固与圆周角有关的知识,做好新旧知识之间的衔接,为本节课新知识的学习做铺垫.通过生活实际问题情境的创设,提出与本节课有关的问题,让学生体会数学与生活密切相关,激发好奇心和求知欲.

探究新知

1.同弧所对的圆周角

师生活动：教师提问，学生分组讨论后回答

如图18所示,∠ACB与∠ADB分别为☉O上同一条弧AB所对的两个圆周角.

（1）∠ACB与∠ADB之间具有怎样的大小关系?

（2）试证明你的猜想.

图18　　　　　　　　　　图19

解:（1）∠ACB=∠ADB.

（2）证明如下:连接OA,OB,如图19所示,

∵∠ACB＝∠AOB,∠ADB＝∠AOB,

∴∠ACB=∠ADB.

【归纳总结】同弧所对的圆周角相等.

2.圆内接四边形及其性质

（1）四个顶点都在同一个圆上的四边形叫做圆内接四边形，这个圆叫做四边形的外接圆.如图所示,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆.

（2）圆内接四边形的性质

师生活动：如图20，四边形ABCD为☉O的内接四边形，☉O为四边形ABCD的外接圆.猜想：∠A与∠C, ∠B与∠D之间的关系为                 .

师生活动：学生先独立思考，再小组内讨论、合作学习，然后教师组织学生交流，进行汇报.

【证明】连接OB，OD.

∵∠A所对的弧为，∠C所对的弧为，

又和所对的圆心角的和是周角，

∴∠A+∠C＝360°÷2＝180°.

同理∠B+∠D＝180°.

（1）　　　　　　　　　　　　（2）

图21

【归纳总结】圆内接四边形的对角互补.

新知应用

例 如图22所示,四边形ABCD为☉O的内接四边形,∠DCE为四边形ABCD的一个外角.求证∠DCE=∠BAD.

证明:∵四边形ABCD为☉O的内接四边形,

∴∠BAD+∠BCD=180°.

∵∠BCD+∠DCE=180°,

∴∠DCE=∠BAD.

【归纳总结】

圆内接四边形的外角等于它的内对角.

课堂练习

1.判断：

（1）同一个圆中等弧所对的圆周角相等.（   ）

（2）相等的弦所对的圆周角也相等.（   ）

（3）同弦所对的圆周角相等.（    ）

2.如图23，在☉O的内接四边形ABCD中，∠BOD＝120°，那么∠BCD是（　　）

A.120°        　　　　　　　　　B.100°     

C.80°         　　　　　　　　　D.60°

图23     　　          图24 

3.如图24，∠A＝50°， ∠ABC＝60 °，BD是☉O的直径，则∠AEB＝（     ）

  A.70°                           B.110°     

C.90°                           D.120°

4.如图25，AB是☉O的直径， C，D是圆上的两点，∠ABD＝40°，则∠BCD＝        .

图25                          图26 

5.如图26，已知圆心角∠AOB＝100°，则圆周角∠ACB＝      ，∠ADB＝        .

参考答案

1.（1）√（2）×（3）×

2.A  3.B   4.50°    5. 130°　50°

课堂小结

1.同弧所对的圆周角相等.

2.圆内接四边形的概念及性质.

布置作业

教材第161页习题A组第1,2题.

教材第162页习题B组第1,2题.

板书设计

28.3   圆心角和圆周角

第3课时

1.同弧所对的圆周角相等.

2.四个顶点都在同一个圆上的四边形叫做圆内接四边形，这个圆叫做四边形的外接圆.

3. 圆内接四边形的性质：（1）圆内接四边形的对角互补；（2）圆内接四边形的外角等于它的内对角.

教学反思

教学反思

教学反思