重庆市第八中学2022-2023学年九年级下学期第一次月考数学试题

重庆八中2022-2023学年度（下）初三

数学试题

（全卷共四个大题，满分150分，考试时间120分钟）

注意事项：

1.试题的答案书写在答题卡上，不得在试题卷上直接作答；

2.作答前认真阅读答题卡上的注意事项；

3.作图（包括作辅助线）请一律用黑色？目铅笔完成；

4.考试结束，由监考人员将试题卷和答题卡一并收回.

参考公式：

一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将等磬卡上题号右侧 正确答案所对应的方框涂黑.

1.的相反数是

A.            B.-3             C.3               D.

2.重庆市统计局发布人口数约为32133000人，用科学记数表示为：

A．3.2133ⅹ107人          B. 3.2133ⅹ106人

C. 32.13ⅹ106人           D.0.32133ⅹ107人

3.下列不是有理数的是

A.        B.          C.          D.0

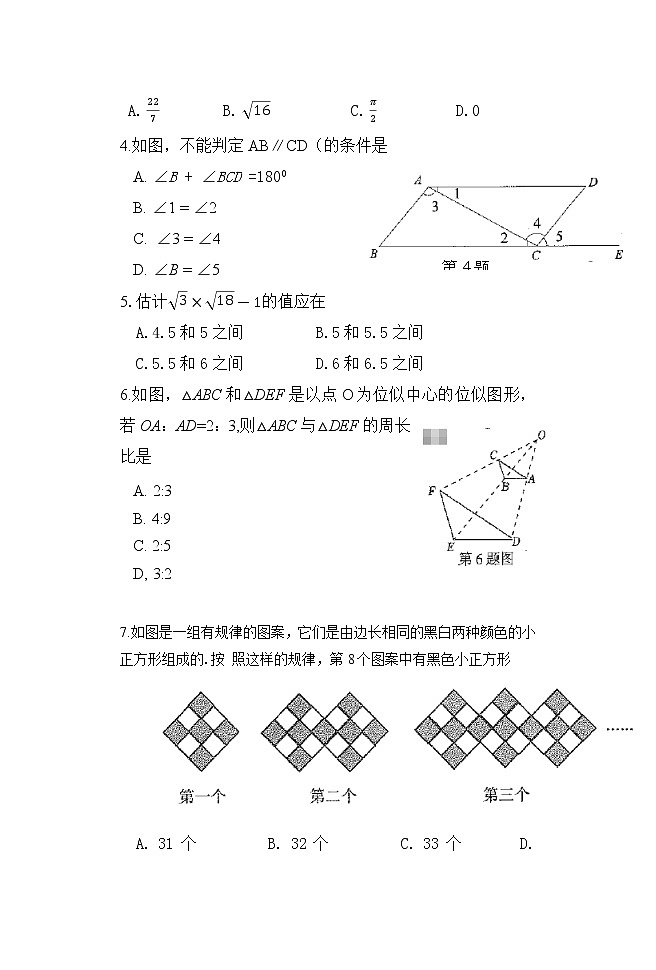
4.如图，不能判定AB∥CD（的条件是

A. ∠B + ∠BCD =1800

B. ∠1 = ∠2

C. ∠3 = ∠4

D. ∠B = ∠5

5.估计的值应在

A.4.5和5之间         B.5和5.5之间

C.5.5和6之间         D.6和6.5之间

6.如图，△ABC和△DEF是以点O为位似中心的位似图形，若OA：AD=2：3,则△ABC与△DEF的周长比是

A. 2:3

B. 4:9

C. 2:5

D, 3:2

7.如图是一组有规律的图案，它们是由边长相同的黑白两种颜色的小正方形组成的.按 照这样的规律，第8个图案中有黑色小正方形

A. 31 个           B. 32 个           C. 33 个         D. 34 个

8. 2021年某市政府投资2亿元人民币建设了公租房7万平方米，预计2023年投资9.5 亿万元人民币建设公租房,若在这两年内每年投资的增长率相同，设年均增长率为工 , 则可列方程组为

A．2（l + x） = 9.5

B．2（l + x） + 2（l + x）2 =9.5

C．2 + 2（l + x） + 2（l + x）2=9.5

D．2（l + x）2 =9.5

9.如图，AB是⊙O的弦，OD为⊙O半径，OC⊥AB,垂足为C, OD//AB, OD =2OC,则∠ODB为

A. 60° 

B. 65°

C. 70°

D. 75°

10.如图，在矩形ABCD中，点E是对角线AC上的中点，过点E作EF⊥EG交DC于点F,交AB于点G.若AD =4, ,则GF 的长度为

A.

B. 5

C.

D. 17

11.若数a使关于x的不等式组有解但最多有三个整数解，且

使关于y的分式方程有整数解，则所有满足条件的整数a的值之和是

A. 11                B. 10           C. 9           D. 8

12.对整式a2+2a进行如下操作：将a2+2a与另一个整式再相加，使得a2+2a与x1的和等于(a+ 2)2,表示为m1= a2+2a + x1 =(a+ 2)2 ,称为第一次操作；将第一次操作的结果m1与另一个整式y1相减，使得m1与y1的差等于a2-2,表示为m2= m1- y1= a2-2,称为第二次操作；将第二次的操作结果m2与另一个整式x2相加，使得加m2与x2的和等于(a+3)2,表示为m3= m2 + x2=(a+ 3)2 ,称为第三次操作；将第三次操作的结果m3与另一个整式y2相减，使得m3与y2的差等于公a2-3,表示为m4=m3-y2= a2-3,称为第四次操作，以此类推，下列四种说法：

① x2 = 6a + 11；     ②y3-x3=1; ③ x2022-y2021 = 2a +1 ；

④当a为奇数时，第n次操作结果为；当n为偶数时，第n次操作结果为；四个结论中正确的有

A. 1个         B. 2个       C. 3个        D. 4个

二、填空题：（本大题4个小题，每小题4分，共16分）请将每小题的答案直接填在等您卡中对应的横线上.

13.计算：=____________.

14.如图，管中放置着三根同样的绳子AA1、BB1、CC1小明和小张两人分别站在管的左右两边并随机选取一根绳子，若每边 每根绳子被选中的机会相等，则两人选到同一根绳子的概率为____________

15.如图，在菱形ABCD中，点E是BC的中点，以C为圆心，CE 为半径作弧，交CQ于点F，连接AE、AF, AB =6, ∠B=60° , 则阴影部分的面积为____________.（结果不取近似值）

16.为了同学们的身体健康，学校初、高中部分别购买了A、B、C三种健身器材.已知初中部购买A、B、C的数量之比为3：4：3, A、B、C的单价之比为2：1：1；高中部购买A种器材比初中部购买A种器材多出的费用占高中部购买三种器材总费用的,高中部购买A种工具的单价比初中部少20% ,高中部购买B种工具超出初中部B种工具的费用与高中部购买C种工具超出初中部购买C种工具的费用之比为2： 3；高中部购买A种工具的费用与购买B种工具的费用之比为4： 3；那么初中部购买A种工具的数量与高中部购买的A种工具的数量之比为____________。

三、解答题：（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的 演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.

17.计算：

（l）              （2）

18.如图，在RT△ABC中，∠ACB =90°； CD⊥AB于点D，AB =EF,且 CB=CE.

（1）用尺规完成以下基本作图：作∠ECH,使∠ECH =∠BCD,交EF于点H（不写作法和证明，保留作图痕迹）

（2）在（1）所作的图形中，求证：CD=CH（请补全下面的证明过程，除题目给的字母外，不添加其它字母或者符号)

证明：

∵∠ACB-900

∴∠ECF=180°-∠ACB =90°

∵在 Rt△ABC和Rt△FEC中

AB =____________①

CB = CE

∴Rt△ABC≌Rt△FEC（HL）

∴∠B =____________②

∵△CBD和△CEH中.

____________③

CB =CE

∠B = ∠ECF

∴____________④

∴CD = CH

四、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.

19.某校近期开展了课外阅读主题周活动，经初步统计，所有学生的课外阅读时长都不低于6小时，但不足12小时，从七，八年级中各随机抽取了20名学生，对他们在活动 期间课外阅读时长（单位：小时）进行整理、描述和分析（阅读时长记为x, 6≤x<7 , 记为6； 7≤x <8,记为7； 8≤x <9,记为8；…以此类推），下面分别给出了抽取的学 生课外阅读时长的部分信息，七年级抽取的学生课外阅读时长：

根据以上信息,解答下列问题:

(1) 填空: a =____________，b =____________，c =____________

（2）该校七年级有800名学生，估计七年级在主题周活动期间课外阅读时长在9小时及 以上的学生人数；

（3）根据以上数据，你认为该校七，八年级学生在主题周活动中，哪个年级学生的阅读 积极性更高？请说明理由.（写出一条理由即可）

20.如图，反比例函数的图象经过点A（-2，2）,一次函数的图象经过点A且与反比例函数图象的另一个交点为B（1，n）.

（1）求一次函数与反比例函数的解析式，并在图中画出该一次函数的图象；

（2）结合图象，直接写出不等式组的解集__________________。

（3）把的图象向下平移4个单位长度,若平移后的直线与反比例函数的图象在第三象限交于 点C（-1,m）,求三角形ABC的面积.

21.露营爱好者在露营时为遮阳和防雨会借助垂直于地面的树干AB搭建一种“天幕”，其截面示意图是轴对称图形，对称轴是垂直于地面的支撑杆CD,用绳子拉直CE后系在 树干AB上的点A处，使得A,C,E在一条直线上，通过调节点A的高度可控制“天幕”的开合，若CE = CF =3米，CD⊥EF于点O

（参考数据：）

⑴天晴时打开“天幕”，若∠ACF=1500，求遮阳宽度EF；（结果保留一位小数）

（2）下雨时收拢“天幕”，∠ACF由1500减小到1200，求点O下降的高度.（结果保留一位小数）

22.甲、乙两支队伍计划自驾去旅游.两队计划同一天出发，沿不同的路线前往目的地汇合.甲队走A路线，全程1600千米，乙队走B路线，全程2000千米，由于B路线高速公路较多，乙队平均每天行驶的路程是甲队的1.5倍，这样乙队用以比甲队提前1天到达目的地.

（1）求甲、乙两队分别多少天到达目的地？

（2）在他们的旅行计划中，乙队每人每天的平均花费始终为336元.甲队最开始计划有13个人同行，计划每人每天花费400元，后来又有若干个人一起加入甲队，经过计 算，甲队实际每增加1人时，每人每天的平均花费将减少40元.若最终甲、乙两队一 起旅行的人数相同，且旅行天数与各自原计划天数一致，两队共需花费48000元，后来有多少人加入甲队？

23.若一个四位数的千位数字与十位数字的差为3,百位数字与个位数字的差为3,则称 这个四位数字n为“珊珊数”；将其千位与百位对调，十位与个位对调得到新数n′，并记M（n）=n - n′,例如：若n = 4311, ∵4-1=3, 3-1≠3，∴4311不是“珊珊数”； 若n = 9360, ∵ 9-6 = 3， 3-0 = 3, ∴9630 是“珊珊数”，加（以）M（n）= 9630 —6903=2727 ；

（1）判断8451, 3303是否是“珊珊数”，请说明理由；如果是，请求出对应的M（n）的值；

（2）若一个四位数是“珊珊数”，且能被33整除,求出所有满足条件的“珊珊数”.

24.如图1,在平面直角坐标系中，抛物线与x轴交于A、B两点（点A 在点B的右侧），与y轴交于点C,OA=4, OB =2,点C（0, -4）, OD=3,连接AD.

（1）求抛物线的解析式；

（2）点F是线段AO上一点，过点F作EF⊥x轴交抛物线于点E,交AD于点M,点N是直线AD上一点，EM =EN,当△EMN的周长最大时，求点E的坐标和此时△EMN周长；

（3）如图2,已知Q（，0）.点P为直线AD上一动点，连接PQ,将抛物线上下平移，平移后的抛物线左侧部分经过点P；当△APQ是以PQ为腰的等腰三角形时，求抛物线的平移距离d.

25.在菱形ABCD中，∠D=60°,点H在平面内，点E为直线上一点.

（1）如图1,当H在AC上时，BE=HE,若AB=4, CH = 3AH ,求CE的长；

（2）如图2,当H在GA延长线上时，HB=HE,O为AC的中点，连接EO并延长交AD 于点G,求证：AH =AG;

（3）如图3, E在直线BC上运动,若∠BHC=300,将△OCE沿OE所在直线翻折至△OC′E, 连接 HC＇，在这个过程中，当ΔC＇OH 的面积取得最大值时，请直接写出的值.