第7章 平行线中作辅助线的方法 冀教版七年级下册专题(含答案)

这是一份第7章 平行线中作辅助线的方法 冀教版七年级下册专题(含答案)，共5页。
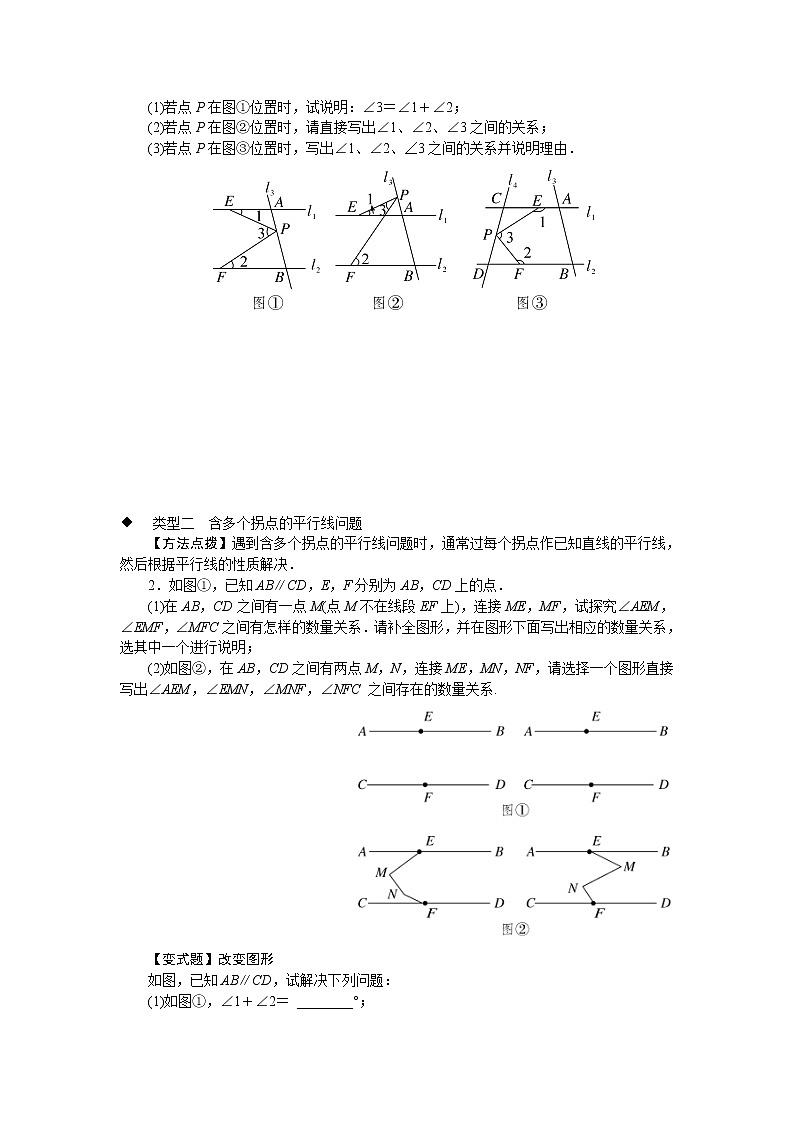
专题：平行线中作辅助线的方法　　 类型一　含一个拐点的平行线问题【方法点拨】在有关图形的计算和推理中，常见一类“折线”“拐角”型问题，解决这类问题的方法是经过拐点作平行线，建立已知角和未知角的联系，从而化“未知”为“已知”．常见的类型有以下几种： 1.阅读下列解题过程，然后解答后面的问题．如图①，已知AB∥CD，∠B＝35°，∠D＝32°，求∠BED的度数．解：过E作EF∥AB，则AB∥CD∥EF.∵AB∥EF，∴∠1＝∠B＝35°.∵CD∥EF，∴∠2＝∠D＝32°.∴∠BED＝∠1＋∠2＝35°＋32°＝67°.然后解答下列问题：如图，是明明设计的智力拼图玩具的一部分，现在明明遇到两个问题，请你帮他解决： (1)如图②，∠D＝30°，∠ACD＝65°，为了保证AB∥DE，∠A应为多大？        (2)如图③，∠G、∠GFH、∠H之间有什么关系时，GP∥HQ?        【变式题】改变图形如图，已知直线l1∥l2，l3、l4和l1、l2分别交于点A、B、C、D，点P 在直线l3或l4上且不与点A、B、C、D重合．记∠AEP＝∠1，∠PFB＝∠2，∠EPF＝∠3.(1)若点P在图①位置时，试说明：∠3＝∠1＋∠2；(2)若点P在图②位置时，请直接写出∠1、∠2、∠3之间的关系；(3)若点P在图③位置时，写出∠1、∠2、∠3之间的关系并说明理由．         类型二　含多个拐点的平行线问题【方法点拨】遇到含多个拐点的平行线问题时，通常过每个拐点作已知直线的平行线，然后根据平行线的性质解决．2．如图①，已知AB∥CD，E，F分别为AB，CD上的点．(1)在AB，CD之间有一点M(点M不在线段EF上)，连接ME，MF，试探究∠AEM，∠EMF，∠MFC之间有怎样的数量关系．请补全图形，并在图形下面写出相应的数量关系，选其中一个进行说明；(2)如图②，在AB，CD之间有两点M，N，连接ME，MN，NF，请选择一个图形直接写出∠AEM，∠EMN，∠MNF，∠NFC 之间存在的数量关系. 【变式题】改变图形如图，已知AB∥CD，试解决下列问题：(1)如图①，∠1＋∠2＝ ________°；(2)如图②，∠1＋∠2＋∠3＝________°；(3)如图③，求∠1＋∠2＋∠3＋∠4的度数；(4)如图④，试探究∠1＋∠2＋∠3＋∠4＋…＋∠n的度数．                               参考答案与解析1．解：(1)∠A＝35°.理由如下：如图②，过C作CM∥DE，则∠1＝∠D＝30°，∴∠2＝∠ACD－∠1＝35°，∴∠2＝∠A，∴CM∥AB.又∵CM∥DE，∴AB∥DE.即∠A＝35°时，AB∥DE.(2)当∠G＋∠GFH＋∠H＝360°时，GP∥HQ.理由如下：如图③，过F作FN∥GP，则∠G＋∠4＝180°.又∵∠G＋∠GFH＋∠H＝360°，∴∠3＋∠H＝180°，∴FN∥HQ，∴GP∥HQ.即∠G＋∠GFH＋∠H＝360°时，GP∥HQ.【变式题】解：(1)如图①，过P作PQ∥l1.∵l1∥l2，∴PQ∥l1∥l2，∴∠1＝∠QPE，∠2＝∠QPF.∵∠3＝∠QPE＋∠QPF，∴∠3＝∠1＋∠2.(2)∠3＝∠2－∠1.　解析：如图②，过P作PQ∥l1.∵l1∥l2，∴PQ∥l2.∴∠1＝∠QPE，∠2＝∠QPF.∵∠3＝∠QPF－∠QPE，∴∠3＝∠2－∠1.(3)∠3＝360°－∠1－∠2.理由如下：如图③，过P作PQ∥l1，∵l1∥l2，∴PQ∥l2.同(1)可证得：∠3＝∠CEP＋∠DFP.∵∠CEP＋∠1＝180°，∠DFP＋∠2＝180°，∴∠CEP＋∠DFP＋∠1＋∠2＝360°，即∠3＝360°－∠1－∠2.2．解：(1)在图①中，∠EMF＝∠AEM＋∠MFC.理由如下：过点M作MP∥AB.∵AB∥CD，∴MP∥CD∥AB，∴∠4＝∠3，∠1＝∠2.∵∠EMF＝∠2＋∠3，∴∠EMF＝∠1＋∠4＝∠AEM＋∠MFC.在图②中，∠AEM＋∠EMF＋∠MFC＝360°.理由如下：过点M作MQ∥AB.∵AB∥CD，∴MQ∥CD∥AB，∴∠CFM＋∠1＝180°，∠AEM＋∠2＝180°，∴∠CFM＋∠1＋∠AEM＋∠2＝360°.∵∠EMF＝∠1＋∠2，∴∠AEM＋∠EMF＋∠MFC＝360°.(2)在图③中，∠EMN＋∠MNF－∠AEM－∠NFC＝180°；在图④中，∠EMN－∠MNF＋∠AEM＋∠NFC＝180°.【变式题】解：(1)180　(2)360(3)如图③，分别过点E，F作EG∥AB，FH∥AB.∵AB∥CD，∴AB∥EG∥FH∥CD，∴∠1＋∠AEG＝180°，∠GEF＋∠EFH＝180°，∠HFC＋∠4＝180°.∴∠1＋∠2＋∠3＋∠4＝540°.(4)如图④，根据上述规律，作(n－2)条辅助线，运用(n－1)次两条直线平行，同旁内角互补，即可得到n个角的和是180°(n－1)．∴∠1＋∠2＋∠3＋∠4＋…＋∠n＝180°(n－1)．