2023年中考苏科版数学一轮复习专题练习-一次函数与反比例函数综合应用

这是一份2023年中考苏科版数学一轮复习专题练习-一次函数与反比例函数综合应用，共6页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
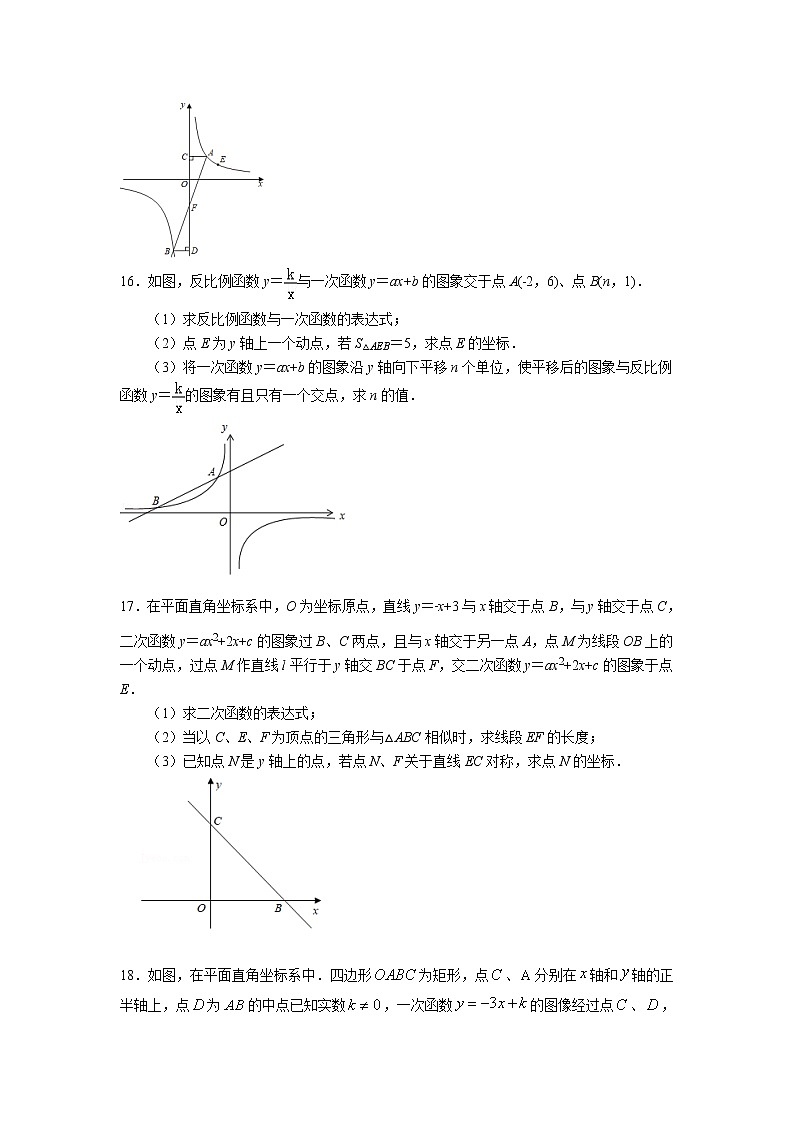
2023年中考数学一轮复习专题练习一次函数与反比例函数综合应用一、选择题1．下列式子：①y=3x−5；②y=；③y=；④y2=x；⑤y=|x|，其中y是x的函数的个数是(　　)A．2个　　　　B．3个　　　　C．4个　　　  D．5个  2．点P（3，﹣1）关于x轴对称的点的坐标是（　　）A．（﹣3，1）    B．（﹣3，﹣1）C．（1，﹣3）    D．（3，1）3.下列函数是反比例函数的是（　　）A．　　　B．　　　C．y＝x2　　　D．y＝2x＋14.在反比例函数的图像上有A（x1，y1），B（x2，y2）两点，x1＜0＜x2，y1＜y2，则m的取值范围是（　　）A．m＞　　　 B．m＜　　　C．m≥　　　D．m≤5．一次函数y＝—2x＋3的图象与坐标轴的交点是                   （    ）A．(3，1)(1，)    B．(1，3)(，1)    C．(3，0)(0，)     D．(0，3)(，0)6．若函数y＝（m+2）x|m|﹣3是反比例函数，则m的值是（　　）A．2       B．﹣2     C．±2       D．不为2的实数7．已知点A（﹣2，y1）、B（﹣1，y2）、C（3，y3）都在反比例函数y＝的图象上，则（　　）A．y1＜y2＜y3 B．y3＜y2＜y1 C．y3＜y1＜y2 D．y2＜y1＜y38. 函数y1＝x和y2＝的图像如图所示，则y1＞y2的x取值范围是（　　）A．x＜－1或x＞1　　　   B．x＜－1或0＜x＜1C．－1＜x＜0或x＞1　　  D．－1＜x＜0或0＜x＜19. 如图，函数y＝－x与函数y＝－的图像相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为C、D，则四边形ACBD的面积为（　　）A．2　　　  B．4　　　　 C．6　　　　 D．8　　　　　第8题　　　　　    第9题　　　　　   二、填空题10．已知直线y＝k1x（k1≠0）与反比例函数y＝（k2≠0）的图象交于M．N两点，若点M的坐标是（1，2），则点N的坐标是　   　．11．如图，直线y1＝x+2与双曲线y2＝交于A（2，m）、B（﹣6，n）两点．则当y1≤y2时，x的取值范围是　   　．12．如图，一次函数y＝x与反比例函数y＝（k＞0）的图象在第一象限交于点A，点C在以B（7，0）为圆心，2为半径的⊙B上，已知AC长的最大值为7，则该反比例函数的函数表达式为　   　．13．如图，直角坐标系xOy中，直线y＝﹣x+b分别交x，y轴的正半轴于点A，B，交反比例函数y＝﹣的图象于点C，D（点C在第二象限内），过点C作CE⊥x轴于点E，记四边形OBCE的面积为S1，△OBD的面积为S2，若，则CD的长为　   　．     14．点A（a，b）是一次函数y＝x﹣2与反比例函数y＝ 的交点，则a2b﹣ab2＝　   　．三、解答题15．如图，点A和点E(2，1)是反比例函数y＝（x＞0）图象上的两点，点B在反比例函数y＝（x＜0）的图象上，分别过点A，B作y轴的垂线，垂足分别为点C，D，AC＝BD，连接AB交y轴于点F．（1）k＝　　；（2）设点A的横坐标为a，点F的纵坐标为m，求证：am＝﹣2；（3）连接CE，DE，当∠CED＝90°时，直接写出点A的坐标：　　．16．如图，反比例函数y＝与一次函数y＝ax+b的图象交于点A(﹣2，6)、点B(n，1)．（1）求反比例函数与一次函数的表达式；（2）点E为y轴上一个动点，若S△AEB＝5，求点E的坐标．（3）将一次函数y＝ax+b的图象沿y轴向下平移n个单位，使平移后的图象与反比例函数y＝的图象有且只有一个交点，求n的值．17．在平面直角坐标系中，O为坐标原点，直线y＝﹣x+3与x轴交于点B，与y轴交于点C，二次函数y＝ax2+2x+c的图象过B、C两点，且与x轴交于另一点A，点M为线段OB上的一个动点，过点M作直线l平行于y轴交BC于点F，交二次函数y＝ax2+2x+c的图象于点E．（1）求二次函数的表达式；（2）当以C、E、F为顶点的三角形与△ABC相似时，求线段EF的长度；（3）已知点N是y轴上的点，若点N、F关于直线EC对称，求点N的坐标． 18．如图，在平面直角坐标系中．四边形为矩形，点、分别在轴和轴的正半轴上，点为的中点已知实数，一次函数的图像经过点、，反比例函数的图像经过点，求的值．已知一次函数y＝kx+b和反比例函数y＝图象相交于A（2，4），B（n，﹣2）两点．（1）求一次函数和反比例函数的解析式；（2）观察图象，直接写出不等式kx+ b﹣  ＜0的解集；（3）点C（a，b），D（a，c）（a＞2）分别在一次函数和反比例函数图象上，且满足CD＝2，求a的值．      20如图，已知反比例函数y＝（x＞0，k是常数）的图象经过点A（1，4），点B（m，n），其中m＞1，AM⊥x轴，垂足为M，BN⊥y轴，垂足为N，AM与BN的交点为C．（1）求出反比例函数解析式；（2）求证：△ACB∽△NOM．（3）延长线段AB，交x轴于点D，若点B恰好为AD的中点，求此时点B的坐标．21.如图，二次函数y＝﹣x2﹣2x+4﹣a2的图象与一次函数y＝﹣2x的图象交于点A、B（点B在右侧），与y轴交于点C，点A的横坐标恰好为a．动点P、Q同时从原点O出发，沿射线OB分别以每秒和2个单位长度运动，经过t秒后，以PQ为对角线作矩形PMQN，且矩形四边与坐标轴平行．（1）求a的值及t＝1秒时点P的坐标；（2）当矩形PMQN与抛物线有公共点时，求时间t的取值范围；（3）在位于x轴上方的抛物线图象上任取一点R，作关于原点（0，0）的对称点为R′，当点M恰在抛物线上时，求R′M长度的最小值，并求此时点R的坐标．       22．如图，在平面直角坐标系中，直线l1：y＝﹣x与反比例函数y＝的图象交于A，B两点（点A在点B左侧），已知A点的纵坐标是2；（1）求反比例函数的表达式；（2）将直线l1：y＝x沿y向上平移后的直线l2与反比例函数y＝在第二象限内交于点C，如果△ABC的面积为30，求平移后的直线l2的函数表达式．         23．如图，在平面直角坐标系中，□ABCO的顶点A在x轴正半轴上，两条对角线相交于点D，双曲线y＝（x＞0）经过C，D两点．（1）求□ABCO的面积．（2）若□ABCO是菱形，请直接写出：①tan∠AOC＝　   　．②将菱形ABCO沿x轴向左平移，当点A与O点重合时停止，则平移距离t与y轴所扫过菱形的面积S之间的函数关系式：　   　． 24．学习了图形的旋转之后，小明知道，将点P绕着某定点A顺时针旋转一定的角度α，能得到一个新的点P′，经过进一步探究，小明发现，当上述点P在某函数图象上运动时，点P′也随之运动，并且点P′的运动轨迹能形成一个新的图形．试根据下列各题中所给的定点A的坐标、角度α的大小来解决相关问题．【初步感知】如图1，设A（1，1），α＝90°，点P是一次函数y＝kx+b图象上的动点，已知该一次函数的图象经过点P1（﹣1，1）．（1）点P1旋转后，得到的点P1′的坐标为 　      　；（2）若点P′的运动轨迹经过点P2′（2，1），求原一次函数的表达式．【深入感悟】如图2，设A（0，0），α＝45°，点P是反比例函数y＝﹣（x＜0）的图象上的动点，过点P′作二、四象限角平分线的垂线，垂足为M，求△OMP′的面积．【灵活运用】如图3，设A（1，﹣），α＝60°，点P是二次函数y＝x2+2x+7图象上的动点，已知点B（2，0）、C（3，0），试探究△BCP′的面积是否有最小值？若有，求出该最小值；若没有，请说明理由．