2020届天津市部分区高三质量调查（一）数学试题 PDF版

天津市部分区2020年高三质量调查试卷（一）

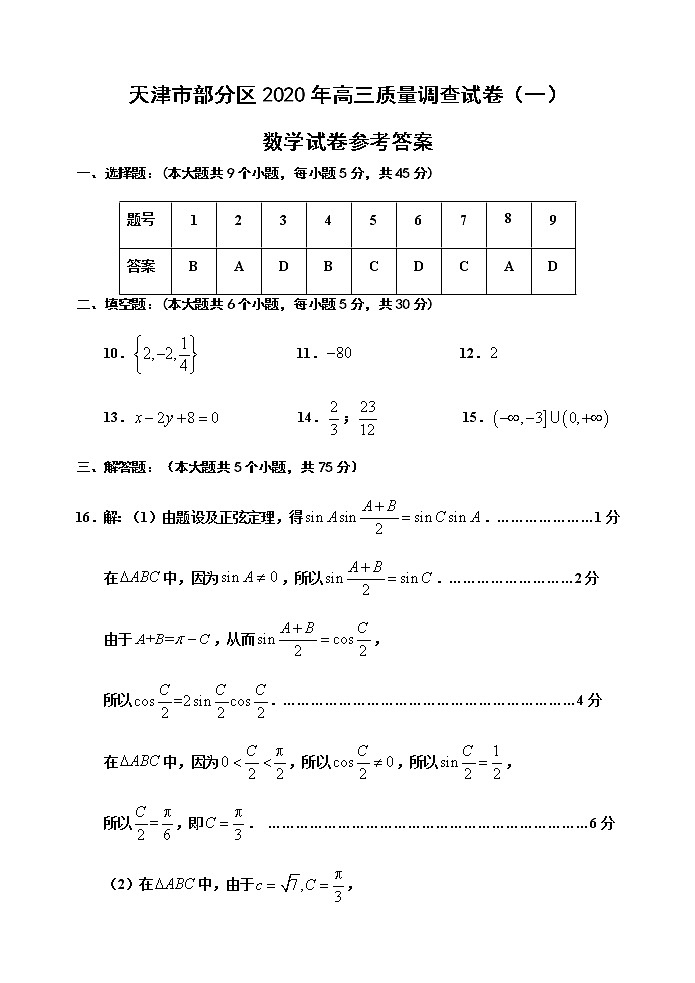
数学试卷参考答案

一、选择题：(本大题共9个小题，每小题5分，共45分)

二、填空题：(本大题共6个小题，每小题5分，共30分)

10．              11．               12．

13．           14．；            15．   

三、解答题：（本大题共5个小题，共75分）

16．解：（1）由题设及正弦定理，得．…………………1分

在中，因为，所以．………………………2分

由于，从而，

所以．………………………………………………………4分

在中，因为，所以，所以，

所以，即． ……………………………………………………………6分                                     

（2）在中，由于，

则由余弦定理，得，即． ……………8分

因为，所以，

解得，从而． …………………………………………………………10分

在中，由正弦定理，得

因为中，，且，所以，

所以． ……………………………12分

所以．

．……………………………14分

17．解：因为四边形，均为正方形，所以．

又，

从而以点为坐标原点，分别以向量

的方向为轴、轴、轴的正方向,建立

如图所示的空间直角坐标系． ……1分

不妨设，则有

，

所以． ………………………2分

（1）证明：【方法一】易知，平面的法向量为．

     由于，所以，即． …………………4分

     又因为平面，所以平面．………………………5分

【说明】本小题的其它解法如下（这里过程略述），若步骤完整、过程严谨，请参照赋分标准，酌情赋分：

【方法二】取的中点,连接．证明平面平面，进而证得

平面．

【方法三】取的中点,连接．先证明,进而证得平

面．

（2）由题意，知,,．

设平面的法向量为，

则有  即

令，得． ……………………………………………………7分

设平面的法向量为，

则有  即

令，得．……………………………………………………8分

所以，所以， ………………10分 

设二面角的大小为，

所以．

故所求二面角的正弦值为．………………………………11分

（3）设点（），则,

且有．

设直线与平面所成角为，

则有，即， ………………12分

整理，得，解得或（舍去）．…………14分

所以． …………………………………………………………15分

18．解：（1）易得，抛物线的焦点的坐标为，准线方程，

所以椭圆的右焦点，左焦点为． ……………………2分

设椭圆的半焦距为,依题意得

   解得． ………………………………………5分

故所求椭圆的方程为． ………………………………………………6分

（2）【方法一】由题意，得的左顶点．

又知直线的斜率存在，不妨设为（），点,

则直线方程为．………………………………………………7分

联立方程组

消去并整理，得， （※）………………9分

易得，

所以点为方程（※）的实数根，

从而，所以．

所以． …………………………11分

由题意，点均在上，且关于原点对称，

所以点,即．………………………12分

因为,所以，解得． ………………………14分

故所求直线的方程为，即． …………………15分

【方法二】由题意，得的左顶点，直线的斜率为，

所以直线的方程为．  ……………………………………………7分

联立方程组

消去并整理，得．

解得，或．………………………………………………………10分

所以点的横坐标（因为为点的横坐标），

所以点的纵坐标，从而点．…………………………12分

由题意，点均在上，且关于原点对称，

所以点的坐标为，所以．………………………………14分

所以直线的方程为,

即所求直线的方程为．…………………………………………15分

19．解：（1）设等比数列公比为，由，

得 消去并整理，得，………………………2分

解得,从而．

所以；  ……………………………………………………………………3分

设等差数列的公差为，由,，

得    …………………………………………………………………5分

解得．

所以．  …………………………………………………6分

（2）由（1）及题意，得其中． ………………8分

①当为奇数时，不妨设数列的前项和为，

所以，

即，   …………………………9分

所以．

上述两式相减，得

      ，  …………11分

所以．  ………………………………………………12分

②当为偶数时，易得，数列前项和为

．………………14分

设{Cn}的前2n项和为T2n

则

．………………………………………15分

20．解：（1）因为（），

所以（）． ……………………………………………1分

因为是的极值点，所以，

即，所以． …………………………………………………………2分

此时，，（）．

易得，当时， ；当时，，

所以函数在区间上单调递减；在区间上单调递增，………4分

所以函数在处的极值是最小值．…………………………………5分

（2）由（1）知，，所以，且．

所以． ……………………………………………………………6分

设（），则． ……………………7分

显然，当时，恒成立，

所以函数在上单调递增，且．………………………9分

所以,当时，，即；

     当时，，即．

所以，函数的单调递减区间为；单调递增区间为． ………11分

（3）证明：由（1）可知,

当时，，即．………………………………12分

不妨令（），

则有（）．……………………………………………13分

所以，

即．…………………………………15分

因为函数在区间上单调递增，

所以（得证）． …………………………………16分