2023版考前三个月冲刺回扣篇　回扣4　立体几何与空间向量

这是一份2023版考前三个月冲刺回扣篇　回扣4　立体几何与空间向量，共12页。
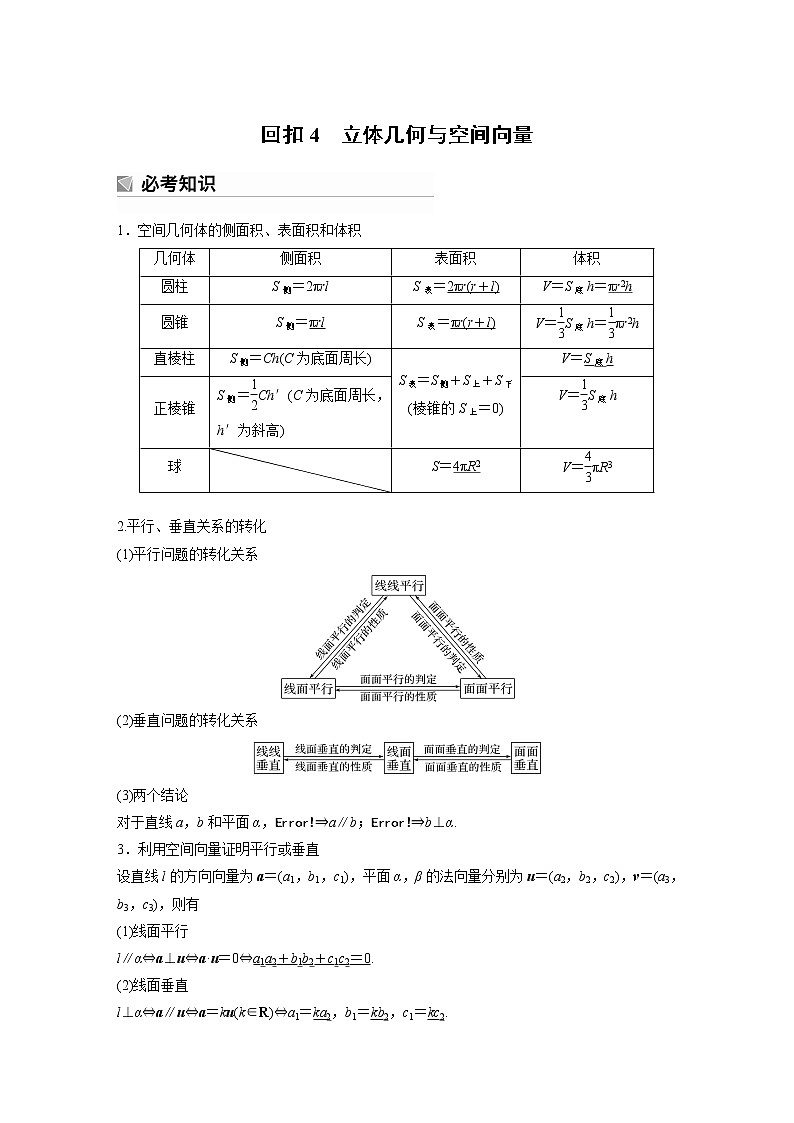
1．空间几何体的侧面积、表面积和体积
2.平行、垂直关系的转化
(1)平行问题的转化关系
(2)垂直问题的转化关系
(3)两个结论
对于直线a，b和平面α，eq \b\lc\ \rc\}(\a\vs4\al\c1(a⊥α,b⊥α))⇒a∥b；eq \b\lc\ \rc\}(\a\vs4\al\c1(a∥b,a⊥α))⇒b⊥α.
3．利用空间向量证明平行或垂直
设直线l的方向向量为a＝(a1，b1，c1)，平面α，β的法向量分别为u＝(a2，b2，c2)，v＝(a3，b3，c3)，则有
(1)线面平行
l∥α⇔a⊥u⇔a·u＝0⇔a1a2＋b1b2＋c1c2＝0.
(2)线面垂直
l⊥α⇔a∥u⇔a＝ku(k∈R)⇔a1＝ka2，b1＝kb2，c1＝kc2.
(3)面面平行
α∥β⇔u∥v⇔u＝λv(λ∈R)⇔a2＝λa3，b2＝λb3，c2＝λc3.
(4)面面垂直
α⊥β⇔u⊥v⇔u·v＝0⇔a2a3＋b2b3＋c2c3＝0.
4．利用空间向量求空间角
(1)设直线l1，l2的夹角为θ，则有cs θ＝|cs〈l1，l2〉|(其中l1，l2分别是直线l1，l2的方向向量)．
(2)设直线l与平面α的夹角为θ，则有sin θ＝|cs〈l，n〉|(其中l是直线l的方向向量，n是平面α的法向量)．
(3)设平面α，β的夹角为θ，则有cs θ＝|cs〈n1，n2〉|(其中n1，n2分别是平面α，β的法向量)．
5．点到平面的距离的求法
(1)定义法：可以利用两个平面垂直作出点到平面的垂线段．
(2)等积法：可以通过换底法把距离问题转化为体积和面积的计算．
(3)向量法：设A是平面α外一点，B是平面α上一点，n是平面α的法向量，则A到平面α的距离是eq \f(|\(AB,\s\up6(→))·n|,|n|).
1．棱锥的平行截面的性质
如果棱锥被平行于底面的平面所截，那么所得的截面与底面相似，截面面积与底面面积的比等于顶点到截面的距离与棱锥高的比的平方．
2．长方体、正方体的内切球和外接球
(1)长方体的体对角线长d与共点的三条棱长a，b，c之间的关系为d2＝a2＋b2＋c2；
若长方体外接球的半径为R，则有(2R)2＝a2＋b2＋c2.
(2)棱长为a的正方体内切球半径r＝eq \f(a,2)，外接球半径R＝eq \f(\r(3),2)a.
3．正四面体的性质
设棱长为a，则正四面体的高h＝eq \f(\r(6),3)a，内切球半径为eq \f(\r(6),12)a，外接球半径为eq \f(\r(6),4)a.
4.球与旋转体的组合通常作轴截面解题．如图所示，设球O的半径为R，截面圆O′的半径为r，M为截面圆上任一点，球心O到截面圆O′的距离为d，则在Rt△OO′M中，OM2＝OO′2＋O′M2，即R2＝d2＋r2.
1．(2022·沈阳模拟)现有一个侧面展开图为半圆形的圆锥，其内部放有一个小球，当小球体积最大时，该圆锥与小球的体积之比是( )
A．9∶4 B．9∶5
C．3∶2 D．3∶1
答案 A
解析 因为圆锥侧面展开图为半圆，
设圆锥母线为l，底面半径为R，
则2πR＝πl，所以l＝2R，
可知圆锥轴截面为正三角形，圆锥高为eq \r(3)R，
当小球是圆锥的内切球时，小球体积最大，轴截面如图所示．
设此时小球半径为r，
则有(eq \r(3)R－r)·sin 30°＝r，
即r＝eq \f(\r(3),3)R，
故V球＝eq \f(4,3)πr3＝eq \f(4,3)π·eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),3)R))3＝eq \f(4\r(3),27)πR3，
V圆锥＝eq \f(1,3)πR2·(eq \r(3)R)＝eq \f(\r(3),3)πR3，
所以V圆锥∶V球＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),3)πR3))∶eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4\r(3),27)πR3))＝9∶4.
2．(多选)(2022·石家庄模拟)设a，b为两条不同的直线，α，β为两个不同的平面，则下列结论不正确的是( )
A．若a∥b，b∥α，则a∥α
B．若a∥b，a∥α，b∥β，则a∥β
C．若a⊥b，a⊥α，b∥β，则α⊥β
D．若a⊥α，b∥α，则a⊥b
答案 ABC
解析 当a⊂α时，a∥b，b∥α可以成立，故A不正确；
当a⊂β时，若a∥b，b⊂α，此时a∥α，b∥β成立，故B不正确；
当α∥β时，若b⊂α，a⊥α，此时a⊥b，b∥β成立，故C不正确，故D正确．
3．(2022·张家口模拟)如图是战国时期的一个铜镞，其由两部分组成，前段是高为2 cm、底面边长为1 cm的正三棱锥，后段是高为0.6 cm的圆柱，圆柱底面圆与正三棱锥底面的正三角形内切，则此铜镞的体积约为(参考数据：π≈3.14，eq \r(3)≈1.732)( )
A．0.25 cm3 B．0.65 cm3
C．0.15 cm3 D．0.45 cm3
答案 D
解析 因为正三棱锥的底面边长为1，
设其内切圆半径为r，由等面积法，
可得eq \f(1,2)×1×1×sin 60°＝eq \f(1,2)×(1＋1＋1)r，
解得r＝eq \f(\r(3),6)，所以其内切圆半径为eq \f(\r(3),6).
由三棱锥体积与圆柱体积公式可得，
V＝eq \f(1,3)×eq \f(1,2)×1×1×sin 60°×2＋π×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(3),6)))2×0.6≈0.45(cm3)．
4．(多选)(2022·济南模拟)在棱长为1的正方体ABCD－A1B1C1D1中，O为正方形A1B1C1D1的中心，则下列结论正确的是( )
A．BO⊥AC
B．BO∥平面ACD1
C．点B到平面ACD1的距离为eq \f(\r(3),3)
D．直线BO与直线AD1的夹角为eq \f(π,3)
答案 ABC
解析 对于A，如图，连接B1D1，A1C1，
则B1D1，A1C1交于点O，
在正方体ABCD－A1B1C1D1中，AC∥A1C1，BB1⊥ 平面A1B1C1D1，A1C1⊂ 平面A1B1C1D1，
故A1C1⊥BB1，而A1C1⊥B1D1，B1D1∩BB1＝B1，B1D1，BB1⊂ 平面BB1D1，
故A1C1⊥平面BB1D1，
故AC⊥平面BB1D1，而BO⊂平面BB1D1，
故AC⊥BO，故A正确；
对于B，连接BD，交AC于E，连接D1E，
则BE∥OD1，BE＝OD1，
故四边形BOD1E是平行四边形，
故BO∥D1E，
又D1E⊂平面ACD1，BO⊄平面ACD1，
则BO∥平面ACD1，故B正确；
对于C，设点B到平面ACD1的距离为d，
因为，
故eq \f(1,3)×eq \f(1,2)×1×1×1
＝eq \f(1,3)×eq \f(1,2)×eq \r(2)×eq \r(2)×sin 60°×d，
解得d＝eq \f(\r(3),3)，故C正确；
对于D，连接BC1，则AD1∥BC1，
∠OBC1即为直线BO与直线AD1的夹角或其补角，
在△BOC1 中，C1O＝eq \f(\r(2),2)，
BO＝eq \r(1＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(2),2)))2)＝eq \f(\r(6),2)，BC1＝eq \r(2)，
所以cs∠OBC1＝eq \f(BO2＋BC\\al(2,1)－OC\\al(2,1),2BO·BC1)
＝eq \f(\f(3,2)＋2－\f(1,2),2×\f(\r(6),2)×\r(2))＝eq \f(\r(3),2)，
则∠OBC1＝eq \f(π,6)，故D错误．
5．(多选)(2022·顺义模拟)如图，设E，F分别是长方体ABCD－A1B1C1D1的棱CD上的两个动点，点E在点F的左边，且满足2EF＝DC＝eq \f(1,2)BC，则下列结论正确的是( )
A．B1D1⊥平面B1EF
B．三棱锥D1－B1EF的体积为定值
C．A1A∥平面B1EF
D．平面A1ADD1⊥平面B1EF
答案 BD
解析 B1D1与D1C1显然不垂直，而EF∥C1D1，因此B1D1与EF显然不垂直，从而B1D1⊥平面B1EF是错误的，A错误；
，在三棱锥B1－D1EF中，平面D1EF即平面CDD1C1，B1到平面CDD1C1的距离为B1C1，是定值，在△D1EF中，EF的长不变，D1到EF的距离不变，面积为定值，因此三棱锥的体积是定值，B正确；
平面B1EF就是平面B1A1DC，而AA1与平面B1A1DC相交，C错误；
长方体中CD⊥平面A1D1DA，CD⊂平面B1A1DC，
所以平面A1D1DA⊥平面B1A1DC，
即平面A1ADD1⊥平面B1EF，D正确．
6．已知过圆锥顶点P的截面为△PAB，O为底面圆的圆心，若二面角P－AB－O的大小为60°，∠AOB＝120°，AB＝2eq \r(3)，则圆锥的侧面积为( )
A.eq \r(3)π B．2eq \r(3)π C.eq \r(7)π D．2eq \r(7)π
答案 D
解析 如图，作OC⊥AB，连接PC，
则C为AB的中点，
∵PB＝PA，∴AB⊥PC，
∴∠PCO即为二面角P－AB－O的平面角，
∴∠PCO＝60°.
在等腰△AOB中，∠AOB＝120°，AB＝2eq \r(3)，
∴AO＝OB＝2，OC＝1，
∴PO＝OC·tan 60°＝eq \r(3).
在Rt△POB中，PB＝eq \r(PO2＋OB2)＝eq \r(7).
∴圆锥的侧面积为π·OB·PB＝2eq \r(7)π.
7．(2022·九江模拟)如图，棱长为3的正方体ABCD－A1B1C1D1中，P为棱CC1上一点，且eq \(CP,\s\up6(→))＝2eq \(PC1,\s\up6(―→))，M为平面BDC1内一动点，则MC＋MP的最小值为 ．
答案 2eq \r(2)
解析 如图，连接A1C，与平面BC1D交于点E，
易知A1C⊥平面BC1D，
作点C关于平面BC1D的对称点N，
易知A1N＝NE＝EC＝eq \f(1,3)A1C＝eq \r(3)，
连接NP，A1C1，由eq \f(CP,CC1)＝eq \f(CN,CA1)＝eq \f(2,3)，
得NP∥A1C1，且NP＝eq \f(2,3)A1C1＝2eq \r(2)，
∴MC＋MP＝MN＋MP≥NP，
当M为NP与平面BC1D的交点时取等号，
则MC＋MP的最小值为2eq \r(2).
8．三棱锥P－ABC中，底面为等边三角形，侧棱长相等，∠APB＝90°，点P到底面ABC的距离为2，则该三棱锥外接球的体积为 ．
答案 36π
解析 因为三棱锥P－ABC中，底面为等边三角形，侧棱长相等，
所以三个侧面均为全等的等腰三角形，
又∠APB＝90°，
即三个侧面均为全等的等腰直角三角形，
所以PA，PB，PC两两互相垂直，且PA＝PB＝PC，
所以可将三棱锥P－ABC补形为正方体，
则该三棱锥的外接球即为正方体的外接球，
设PA＝PB＝PC＝a，
则AB＝AC＝BC＝eq \r(2)a，
又点P到底面ABC的距离为2，
所以由eq \f(1,3)S△ABC×2＝eq \f(1,3)S△PBC×PA，
即eq \f(1,3)×eq \f(\r(3),4)(eq \r(2)a)2×2＝eq \f(1,3)×eq \f(1,2)a×a×a，
解得a＝2eq \r(3)，
所以正方体的外接球直径2R＝eq \r(a2＋a2＋a2)＝eq \r(2\r(3)2＋2\r(3)2＋2\r(3)2)＝6，即R＝3，
所以该三棱锥外接球的体积为
V＝eq \f(4,3)πR3＝eq \f(4,3)π×33＝36π.
9.如图，在三棱柱ABC－A1B1C1中，AB＝4，∠BAC＝30°，侧面BCC1B1是正方形，E是BB1的中点，CE＝eq \r(5)，CE⊥AC.
(1)求证：CC1⊥AC；
(2)F是线段AC1上的点，若平面ABC与平面CEF的夹角为45°，求AF的长．
(1)证明 因为四边形BCC1B1是正方形，E为BB1的中点，CE＝eq \r(5)，所以BC＝2.
在△ABC中，由正弦定理得，
sin∠ACB＝eq \f(ABsin∠BAC,BC)＝eq \f(4×sin 30°,2)＝1，
所以∠ACB＝90°，即AC⊥BC.
因为AC⊥CE，BC∩CE＝C，
BC⊂平面BCC1B1，CE⊂平面BCC1B1，
所以AC⊥平面BCC1B1.
又因为CC1⊂平面BCC1B1，
所以AC⊥CC1.
(2)解 由(1)得AC＝2eq \r(3)，BC＝CC1＝2，AC1＝4，AC，BC，CC1两两垂直．
以C为原点，CA，CB，CC1所在直线分别为x轴、y轴、z轴，建立如图所示的空间直角坐标系，
则C(0,0,0)，E(0,2,1)，
A(2eq \r(3)，0,0)，C1(0,0,2)，
于是eq \(CE,\s\up6(→))＝(0,2,1)，eq \(CA,\s\up6(→))＝(2eq \r(3)，0,0)，
eq \(AC1,\s\up6(―→))＝(－2eq \r(3)，0,2)．
设eq \(AF,\s\up6(→))＝λeq \(AC1,\s\up6(―→))，λ∈[0,1)，
则eq \(CF,\s\up6(→))＝eq \(CA,\s\up6(→))＋λeq \(AC1,\s\up6(―→))＝(2eq \r(3)－2eq \r(3)λ，0,2λ)，
设平面CEF的法向量为n＝(x，y，z)，
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(CE,\s\up6(→))＝0，,n·\(CF,\s\up6(→))＝0，)) 即eq \b\lc\{\rc\ (\a\vs4\al\c1(2y＋z＝0，,2\r(3)－2\r(3)λx＋2λz＝0，))
令z＝－2，得n＝eq \b\lc\(\rc\)(\a\vs4\al\c1( \f(2λ,\r(3)－\r(3)λ)，1，－2)).
平面ABC的一个法向量为m＝(0,0,1)．
所以cs〈m，n〉＝eq \f(m·n,|m||n|)
＝eq \f(－2,\r(\b\lc\(\rc\)(\a\vs4\al\c1( \f(2λ,\r(3)－\r(3)λ)))2＋12＋－22))，
由平面ABC与平面CEF的夹角为45°，
得|cs〈m，n〉|＝cs 45°，
即eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(－2,\r(\b\lc\(\rc\)(\a\vs4\al\c1( \f(2λ,\r(3)－\r(3)λ)))2＋12＋－22))))＝eq \f(\r(2),2)，
解得λ＝eq \f(3,5)(λ＝3舍去)，
则AF＝eq \f(3,5)AC1＝eq \f(3,5)×4＝eq \f(12,5).
10.在菱形ABCD中，∠ABC＝120°，EA⊥平面ABCD，EA∥FD，EA＝AD＝2FD＝2，
(1)证明：直线FC∥平面EAB；
(2)求平面EFC与平面FCA夹角的正弦值；
(3)线段EC上是否存在点M使得直线EB与平面BDM所成角的正弦值为eq \f(\r(2),8)？若存在，求eq \f(EM,MC)；若不存在，说明理由．
(1)证明 以D为原点，分别以DA，DT(T为BC中点)，DF所在直线为x轴、y轴、z轴建立如图所示的空间直角坐标系，
则A(2,0,0)，B(1，eq \r(3)，0)，C(－1，eq \r(3)，0)，
D(0,0,0)，E(2,0,2)，F(0,0,1)．
eq \(EA,\s\up6(→))＝(0,0，－2)，eq \(AB,\s\up6(→))＝(－1，eq \r(3)，0)，
设n＝(x，y，z)为平面EAB的法向量，
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n·\(EA,\s\up6(→))＝0，,n·\(AB,\s\up6(→))＝0，))即eq \b\lc\{\rc\ (\a\vs4\al\c1(－2z＝0，,－x＋\r(3)y＝0，))
可得n＝(eq \r(3)，1,0)，又eq \(FC,\s\up6(→))＝(－1，eq \r(3)，－1)，
可得n·eq \(FC,\s\up6(→))＝0，
又因为直线FC⊄平面EAB，
所以直线FC∥平面EAB.
(2)解 eq \(EF,\s\up6(→))＝(－2,0，－1)，
eq \(FC,\s\up6(→))＝(－1，eq \r(3)，－1)，eq \(FA,\s\up6(→))＝(2,0，－1)，
设n1＝(x1，y1，z1)为平面EFC的法向量，
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n1·\(EF,\s\up6(→))＝0，,n1·\(FC,\s\up6(→))＝0，))即eq \b\lc\{\rc\ (\a\vs4\al\c1(－2x1－z1＝0，,－x1＋\r(3)y1－z1＝0，))
可得n1＝(－3，eq \r(3)，6)，
设n2＝(x2，y2，z2)为平面FCA的法向量，
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n2·\(FA,\s\up6(→))＝0，,n2·\(FC,\s\up6(→))＝0，))即eq \b\lc\{\rc\ (\a\vs4\al\c1(2x2－z2＝0，,－x2＋\r(3)y2－z2＝0，))
可得n2＝(1，eq \r(3)，2)，
所以|cs〈n1，n2〉|＝eq \f(|n1·n2|,|n1||n2|)＝eq \f(\r(6),4)，
则sin〈n1，n2〉＝eq \r(1－cs2〈n1，n2〉)＝eq \f(\r(10),4)，
所以平面EFC与平面FCA夹角的正弦值为eq \f(\r(10),4).
(3)解 由题意可得，eq \(EC,\s\up6(→))＝(－3，eq \r(3)，－2)，
设eq \(EM,\s\up6(→))＝λeq \(EC,\s\up6(→))＝(－3λ，eq \r(3)λ，－2λ)，
则M(2－3λ，eq \r(3)λ，2－2λ)，
则eq \(BD,\s\up6(→))＝(－1，－eq \r(3)，0)，
eq \(DM,\s\up6(→))＝(2－3λ，eq \r(3)λ，2－2λ)，
设n3＝(x3，y3，z3)为平面BDM的法向量，
则eq \b\lc\{\rc\ (\a\vs4\al\c1(n3·\(BD,\s\up6(→))＝0，,n3·\(DM,\s\up6(→))＝0，))
即eq \b\lc\{\rc\ (\a\vs4\al\c1(－x3－\r(3)y3＝0，,2－3λx3＋\r(3)λy3＋2－2λz3＝0，))
可得n3＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\r(3)，－1，\f(2\r(3)λ－\r(3),1－λ)))，
由eq \(EB,\s\up6(→))＝(－1，eq \r(3)，－2)，
得|cs〈eq \(EB,\s\up6(→))，n3〉|＝eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(－2\r(3)－2×\f(2\r(3)λ－\r(3),1－λ),2\r(2)×\r(4＋\b\lc\(\rc\)(\a\vs4\al\c1(\f(2\r(3)λ－\r(3),1－λ)))2))))
＝eq \f(\r(2),8)，
解得λ＝eq \f(1,4)或λ＝－eq \f(7,8)(舍)，
所以eq \f(EM,MC)＝eq \f(1,3).几何体
侧面积
表面积
体积
圆柱
S侧＝2πrl
S表＝2πr(r＋l)
V＝S底h＝πr2h
圆锥
S侧＝πrl
S表＝πr(r＋l)
V＝eq \f(1,3)S底h＝eq \f(1,3)πr2h
直棱柱
S侧＝Ch(C为底面周长)
S表＝S侧＋S上＋S下(棱锥的S上＝0)
V＝S底h
正棱锥
S侧＝eq \f(1,2)Ch′(C为底面周长，h′为斜高)
V＝eq \f(1,3)S底h
球
S＝4πR2
V＝eq \f(4,3)πR3