

所属成套资源:2023版考前三个月冲刺回扣篇
2023版考前三个月冲刺回扣篇 回扣6 解析几何
展开这是一份2023版考前三个月冲刺回扣篇 回扣6 解析几何,共11页。
1.两条直线的位置关系
2.圆的三种方程
(1)圆的标准方程:(x-a)2+(y-b)2=r2(r>0).
(2)圆的一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0).
(3)圆的直径式方程:(x-x1)(x-x2)+(y-y1)(y-y2)=0(A(x1,y1),B(x2,y2)是圆的直径的两端点).
3.三种距离公式
(1)A(x1,y1),B(x2,y2)两点的距离
|AB|=eq \r(x2-x12+y2-y12).
(2)点到直线的距离d=eq \f(|Ax0+By0+C|,\r(A2+B2))(其中点P(x0,y0),直线方程为Ax+By+C=0).
(3)两平行线间的距离d=eq \f(|C2-C1|,\r(A2+B2))(其中两平行线方程分别为l1:Ax+By+C1=0,
l2:Ax+By+C2=0).
4.直线与圆的位置关系
直线l:Ax+By+C=0和圆C:(x-a)2+(y-b)2=r2(r>0)有相交、相离、相切三种情况.可从代数和几何两个方面来判断:
(1)代数法(即判断直线与圆的方程联立所得方程组的解的情况):Δ>0⇔相交;Δ<0⇔相离;Δ=0⇔相切.
(2)几何法(即比较圆心到直线的距离与半径的大小):设圆心到直线的距离为d,则d
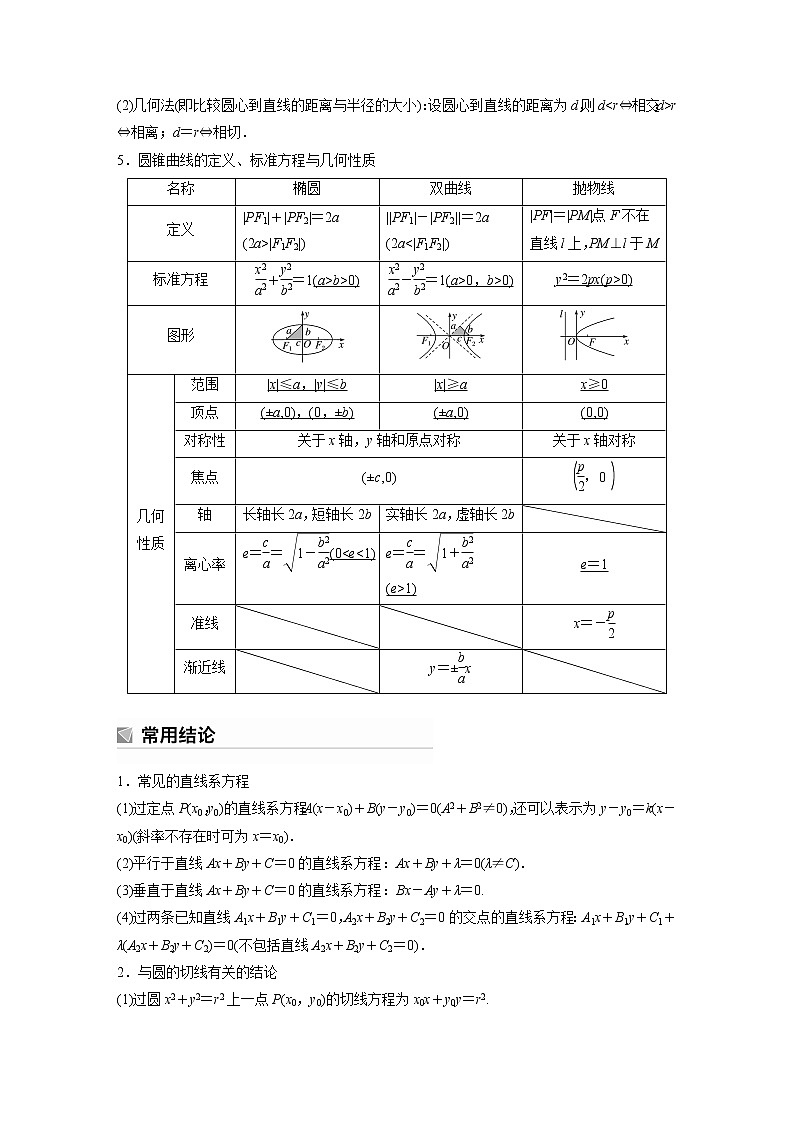
5.圆锥曲线的定义、标准方程与几何性质
1.常见的直线系方程
(1)过定点P(x0,y0)的直线系方程:A(x-x0)+B(y-y0)=0(A2+B2≠0),还可以表示为y-y0=k(x-x0)(斜率不存在时可为x=x0).
(2)平行于直线Ax+By+C=0的直线系方程:Ax+By+λ=0(λ≠C).
(3)垂直于直线Ax+By+C=0的直线系方程:Bx-Ay+λ=0.
(4)过两条已知直线A1x+B1y+C1=0,A2x+B2y+C2=0的交点的直线系方程:A1x+B1y+C1+λ(A2x+B2y+C2)=0(不包括直线A2x+B2y+C2=0).
2.与圆的切线有关的结论
(1)过圆x2+y2=r2上一点P(x0,y0)的切线方程为x0x+y0y=r2.
(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的切线方程为(x0-a)(x-a)+(y0-b)·(y-b)=r2.
(3)过圆x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点为A,B,则过A,B两点的直线方程为x0x+y0y=r2.
3.两圆公共弦
两个圆的方程相减得到的二元一次方程即为两圆公共弦所在的直线方程.
4.通径
(1)椭圆通径长为eq \f(2b2,a).
(2)双曲线通径长为eq \f(2b2,a).
(3)抛物线通径长为2p.
5.双曲线的方程与渐近线方程的关系
(1)若双曲线的方程为eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0),则渐近线的方程为eq \f(x2,a2)-eq \f(y2,b2)=0,即y=±eq \f(b,a)x.
(2)若渐近线的方程为y=±eq \f(b,a)x,即eq \f(x,a)±eq \f(y,b)=0,则双曲线的方程可设为eq \f(x2,a2)-eq \f(y2,b2)=λ.
(3)若所求双曲线与双曲线eq \f(x2,a2)-eq \f(y2,b2)=1有公共渐近线,其方程可设为eq \f(x2,a2)-eq \f(y2,b2)=λ(λ>0,焦点在x轴上;λ<0,焦点在y轴上).
(4)焦点到渐近线的距离总是b.
6.抛物线焦点弦的常用结论
设AB是过抛物线y2=2px(p>0)焦点F的弦,若A(x1,y1),B(x2,y2),α为直线AB的倾斜角,且y1>0>y2,则
(1)焦半径|AF|=x1+eq \f(p,2)=eq \f(p,1-cs α),
|BF|=x2+eq \f(p,2)=eq \f(p,1+cs α).
(2)x1x2=eq \f(p2,4),y1y2=-p2.
(3)弦长|AB|=x1+x2+p=eq \f(2p,sin2α).
(4)eq \f(1,|FA|)+eq \f(1,|FB|)=eq \f(2,p).
(5)以弦AB为直径的圆必与准线相切.
(6)S△OAB=eq \f(p2,2sin α)(O为抛物线的顶点).
1.(2022·淄博模拟)已知条件p:直线x+2y-1=0与直线a2x+(a+1)y-1=0平行,条件q:a=1,则p是q的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
答案 D
解析 当直线x+2y-1=0与直线a2x+(a+1)·y-1=0平行时,
eq \f(a2,1)=eq \f(a+1,2)≠1,解得a=-eq \f(1,2),
当a=1时,直线x+2y-1=0与直线a2x+(a+1)y-1=0重合,
所以p是q的既不充分也不必要条件.
2.已知圆C:x2+y2+2ay=0(a>0)截直线eq \r(3)x-y=0所得的弦长为2eq \r(3),则圆C与圆C′:(x-1)2+(y+1)2=1的位置关系是( )
A.相离 B.外切 C.相交 D.内切
答案 C
解析 圆C的圆心为(0,-a),半径为a,
其圆心到直线eq \r(3)x-y=0的距离为eq \f(|a|,\r(3+1))=eq \f(a,2),
所截得的弦长为2eq \r(a2-\b\lc\(\rc\)(\a\vs4\al\c1(\f(a,2)))2)=eq \r(3)a=2eq \r(3),解得a=2.
所以圆C的标准方程为x2+(y+2)2=4,C的圆心为(0,-2),半径为2.
又C′的圆心为(1,-1),半径为1,
|CC′|=eq \r(0-12+-2+12)=eq \r(2),
故可得2-1<|CC′|<2+1,则两圆的位置关系是相交.
3.设F1,F2分别是双曲线eq \f(x2,4)-eq \f(y2,45)=1的左、右焦点,P是该双曲线上的一点,且3|PF1|=5|PF2|,则△PF1F2的面积等于( )
A.14eq \r(3) B.7eq \r(15)
C.15eq \r(3) D.5eq \r(15)
答案 C
解析 设|PF1|=5x,|PF2|=3x,
则由双曲线的定义可得,
|PF1|-|PF2|=5x-3x=2x=2a=4,
所以x=2,故|PF1|=10,|PF2|=6,
又|F1F2|=14,
故cs∠F1PF2=eq \f(100+36-196,2×10×6)=-eq \f(1,2),
故sin∠F1PF2=eq \f(\r(3),2),
所以△PF1F2的面积为
eq \f(1,2)×10×6×eq \f(\r(3),2)=15eq \r(3).
4.(多选)(2022·南京模拟)已知抛物线y2=4x的焦点为F,过原点O的动直线l交抛物线于另一点P,交抛物线的准线于点Q,下列说法正确的是( )
A.若O为线段PQ的中点,则|PF|=2
B.若|PF|=4,则|OP|=2eq \r(5)
C.存在直线l,使得PF⊥QF
D.△PFQ面积的最小值为2
答案 AD
解析 抛物线y2=4x的准线为x=-1,
焦点F(1,0),
若O为PQ的中点,
则xP=1,
所以|PF|=xP+1=2,
故A正确;
若|PF|=4,则xP=4-1=3,
所以|OP|=eq \r(x\\al(2,P)+y\\al(2,P))=eq \r(x\\al(2,P)+4xP)=eq \r(21),故B错误;
设P(a2,2a),则Qeq \b\lc\(\rc\)(\a\vs4\al\c1(-1,-\f(2,a))),
所以eq \(FP,\s\up6(→))=(a2-1,2a),eq \(QF,\s\up6(→))=eq \b\lc\(\rc\)(\a\vs4\al\c1(2,\f(2,a))),
所以eq \(FP,\s\up6(→))·eq \(QF,\s\up6(→))=2a2-2+4=2a2+2>0,
所以FP与FQ不垂直,故C错误;
S△PFQ=eq \f(1,2)·|OF|·|yP-yQ|=eq \f(1,2)×1×eq \b\lc\|\rc\|(\a\vs4\al\c1(2a+\f(2,a)))=|a|+eq \f(1,|a|)≥2,
当且仅当|a|=eq \f(1,|a|),即a=±1时,取等号,
所以△PFQ面积的最小值为2,故D正确.
5.(多选)(2022·青岛模拟)已知椭圆C:eq \f(x2,4)+eq \f(y2,3)=1的左、右焦点分别是F1,F2,Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3),y0))为椭圆C上一点,则下列结论正确的是( )
A.△MF1F2的周长为6
B.△MF1F2的面积为eq \f(\r(15),3)
C.△MF1F2的内切圆的半径为eq \f(\r(15),9)
D.△MF1F2的外接圆的直径为eq \f(32,11)
答案 ABC
解析 椭圆C:eq \f(x2,4)+eq \f(y2,3)=1的左、右焦点分别是F1(-1,0),F2(1,0),
因为Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3),y0))为椭圆C上一点,
则eq \f(\b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)))2,4)+eq \f(y\\al(2,0),3)=1,解得|y0|=eq \f(\r(15),3),
所以|MF1|=eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(7,3)))2+\b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(15),3)))2)=eq \f(8,3),
|MF2|=4-eq \f(8,3)=eq \f(4,3).
所以△MF1F2的周长为2a+2c=4+2=6,A正确;
△MF1F2的面积为eq \f(1,2)×2c×|y0|=c×|y0|
=1×eq \f(\r(15),3)=eq \f(\r(15),3),B正确;
设△MF1F2的内切圆的半径为r,
则eq \f(1,2)×6×r=eq \f(\r(15),3),r=eq \f(\r(15),9),C正确;
cs∠F1MF2=eq \f(\f(64,9)+\f(16,9)-4,2×\f(8,3)×\f(4,3))=eq \f(11,16)>0,
所以∠F1MF2为锐角,
sin∠F1MF2=eq \r(1-\f(121,256))=eq \f(\r(135),16)=eq \f(3\r(15),16),
所以△MF1F2的外接圆的直径为eq \f(|F1F2|,sin∠F1MF2)=eq \f(2,\f(3\r(15),16))=eq \f(32,3\r(15))=eq \f(32\r(15),45),D错误.
6.已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点,且|FA|·|FB|=6,则|AB|=________.
答案 6
解析 设抛物线的准线为l,则l=-1,
|FA|=m,|FB|=n,
分别过点A,B作AA1⊥l于点A1,BB1⊥l于点B1,
由三角形相似定理得,
eq \f(m,n)=eq \f(m-2,2-n),即2(m+n)=2mn=12,
所以m+n=6,即|AB|=6.
7.已知直线l过点P(0,1),且与圆O:x2+y2=3相交于A,B两点,设eq \(OC,\s\up6(→))=eq \(OA,\s\up6(→))+eq \(OB,\s\up6(→)),若点C在圆O上,则直线l的倾斜角为________.
答案 30°或150°
解析 因为eq \(OC,\s\up6(→))=eq \(OA,\s\up6(→))+eq \(OB,\s\up6(→)),|OA|=|OB|,
则四边形OACB为菱形,所以OC⊥AB.
设D为垂足,因为点C在圆O上,
则|OD|=eq \f(|OC|,2)=eq \f(\r(3),2).
设直线l的方程为y=kx+1,
由eq \f(1,\r(k2+1))=eq \f(\r(3),2),
得k2=eq \f(1,3),即k=±eq \f(\r(3),3),
设倾斜角为α,则tan α=±eq \f(\r(3),3),
因为α∈(0,π),
所以直线l的倾斜角为30°或150°.
8.(2022·石家庄模拟)已知椭圆C1和双曲线C2有公共的焦点F1,F2,曲线C1和C2在第一象限相交于点P,且∠F1PF2=60°.若椭圆C1的离心率的取值范围是eq \b\lc\[\rc\](\a\vs4\al\c1(\f(\r(3),3),\f(\r(2),2))),则双曲线C2的离心率的取值范围是________.
答案 eq \b\lc\[\rc\](\a\vs4\al\c1(\f(\r(6),2),\r(3)))
解析 设椭圆C1:eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0),
双曲线C2:eq \f(x2,a\\al(2,1))-eq \f(y2,b\\al(2,1))=1(a1>0,b1>0),
椭圆与双曲线的半焦距为c,
椭圆离心率e=eq \f(c,a),
双曲线离心率e1=eq \f(c,a1),
如图,设|PF1|=s,
|PF2|=t,
由椭圆定义可得,s+t=2a,由双曲线定义可得,
s-t=2a1,
联立可得s=a1+a,t=a-a1,
由余弦定理得,
4c2=s2+t2-2stcs∠F1PF2
=(a+a1)2+(a-a1)2-2(a+a1)·(a-a1)cs 60°
=a2+3aeq \\al(2,1),
即4=eq \f(1,e2)+eq \f(3,e\\al(2,1)),
解得eeq \\al(2,1)=eq \f(3,4-\f(1,e2)),
因为e∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(\r(3),3),\f(\r(2),2))),
所以eq \f(1,3)≤e2≤eq \f(1,2),2≤eq \f(1,e2)≤3,
可得eq \f(3,2)≤eeq \\al(2,1)≤3,
故eq \f(\r(6),2)≤e1≤eq \r(3).
9.已知椭圆C:eq \f(y2,a2)+eq \f(x2,b2)=1(a>b>0)的离心率e=eq \f(1,2),左、右顶点分别为曲线y=2x2-6与x轴的交点.
(1)求椭圆C的方程;
(2)过C的下焦点作一条斜率为k的直线l,l与椭圆C相交于点A与B,O为坐标原点,求△OAB面积的最大值.
解 (1)设椭圆的半焦距为c(c>0).
由曲线y=2x2-6与x轴的交点,
可得椭圆C的左、右顶点分别为(-eq \r(3),0),(eq \r(3),0),即b=eq \r(3),
椭圆的离心率e=eq \f(1,2),
即eq \f(c,a)=eq \f(1,2),
因为a2=b2+c2,
所以a2=3+eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)a))2,
解得a2=4,所以a=2,c=1,
所以椭圆C的方程为eq \f(y2,4)+eq \f(x2,3)=1.
(2)由(1)可知椭圆C的下焦点为(0,-1),故l的方程为y=kx-1,
由eq \b\lc\{\rc\ (\a\vs4\al\c1(y=kx-1,,\f(y2,4)+\f(x2,3)=1,))消去y可得
(3k2+4)x2-6kx-9=0,
设A(x1,y1),B(x2,y2),
则x1+x2=eq \f(6k,3k2+4),x1x2=-eq \f(9,3k2+4),
所以|AB|=eq \r(1+k2)·eq \r(x1+x22-4x1x2)
=eq \r(k2+1)·eq \r(\b\lc\(\rc\)(\a\vs4\al\c1(\f(6k,3k2+4)))2+\f(36,3k2+4))
=eq \f(12k2+1,3k2+4).
又O到l:kx-y-1=0的距离为d=eq \f(1,\r(k2+1)),
所以S△OAB=eq \f(1,2)|AB|d
=eq \f(6k2+1,3k2+4)·eq \f(1,\r(k2+1))
=eq \f(6\r(k2+1),3k2+4).
令t=eq \r(k2+1)≥1,则k2=t2-1,
则S△OAB=eq \f(6t,3t2+1)=eq \f(6,3t+\f(1,t)).
对于函数y=3t+eq \f(1,t)(t≥1),
y′=3-eq \f(1,t2)=eq \f(3t2-1,t2)>0,
即函数y=3t+eq \f(1,t)(t≥1)在t∈[1,+∞)上单调递增,
所以当t=1,k=0时,y=3t+eq \f(1,t)取得最小值4,
此时S△OAB取得最大值eq \f(3,2).
10.已知双曲线C:eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0)的离心率是eq \f(\r(5),2),实轴长是8.
(1)求双曲线C的方程;
(2)过点P(0,3)的直线l与双曲线C的右支交于不同的两点A和B,若直线l上存在不同于点P的点D满足|PA|·|DB|=|PB|·|DA|成立,证明:点D的纵坐标为定值,并求出该定值.
解 (1)依题意得eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(c,a)=\f(\r(5),2),,2a=8,,c2=a2+b2,))解得eq \b\lc\{\rc\ (\a\vs4\al\c1(a2=16,,b2=4,))
所以双曲线C的方程是eq \f(x2,16)-eq \f(y2,4)=1.
(2)设A(x1,y1),B(x2,y2),D(x0,y0),直线l的方程为y=kx+3,
将直线方程y=kx+3代入双曲线方程eq \f(x2,16)-eq \f(y2,4)=1,
化简整理得(1-4k2)x2-24kx-52=0,
Δ=(-24k)2+4×(1-4k2)×52=208-256k2,
则x1+x2=eq \f(24k,1-4k2),x1x2=-eq \f(52,1-4k2).
要使直线与双曲线的右支有两个不同的交点A和B,
则应满足eq \b\lc\{\rc\ (\a\vs4\al\c1(1-4k2≠0,,Δ>0,,x1+x2>0,,x1x2>0,))即eq \b\lc\{\rc\ (\a\vs4\al\c1(1-4k2≠0,,208-256k2>0,,\f(24k,1-4k2)>0,,-\f(52,1-4k2)>0,))
解得-eq \f(\r(13),4)
得eq \f(|PA|,|PB|)=eq \f(|DA|,|DB|),
故eq \f(x1,x2)=eq \f(x0-x1,x2-x0),
所以x0=eq \f(2x1x2,x1+x2)=eq \f(\f(-104,1-4k2),\f(24k,1-4k2))=-eq \f(13,3k).
又y0=kx0+3=-eq \f(13,3)+3=-eq \f(4,3),
所以点D的纵坐标为定值-eq \f(4,3).斜截式
一般式
直线方程
y=k1x+b1,
y=k2x+b2
A1x+B1y+C1=0,
A2x+B2y+C2=0
相交
k1≠k2
A1B2-A2B1≠0
垂直
k1k2=-1
A1A2+B1B2=0
平行
k1=k2且b1≠b2
eq \b\lc\{\rc\ (\a\vs4\al\c1(A1B2-A2B1=0,,B1C2-B2C1≠0))
或eq \b\lc\{\rc\ (\a\vs4\al\c1(A1B2-A2B1=0,,A1C2-A2C1≠0))
重合
k1=k2且b1=b2
A1B2-A2B1
=B1C2-B2C1
=A1C2-A2C1=0
名称
椭圆
双曲线
抛物线
定义
|PF1|+|PF2|=2a
(2a>|F1F2|)
||PF1|-|PF2||=2a
(2a<|F1F2|)
|PF|=|PM|点F不在直线l上,PM⊥l于M
标准方程
eq \f(x2,a2)+eq \f(y2,b2)=1(a>b>0)
eq \f(x2,a2)-eq \f(y2,b2)=1(a>0,b>0)
y2=2px(p>0)
图形
几何
性质
范围
|x|≤a,|y|≤b
|x|≥a
x≥0
顶点
(±a,0),(0,±b)
(±a,0)
(0,0)
对称性
关于x轴,y轴和原点对称
关于x轴对称
焦点
(±c,0)
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(p,2),0))
轴
长轴长2a,短轴长2b
实轴长2a,虚轴长2b
离心率
e=eq \f(c,a)=eq \r(1-\f(b2,a2))(0
(e>1)
e=1
准线
x=-eq \f(p,2)
渐近线
y=±eq \f(b,a)x
相关学案
这是一份2023版考前三个月冲刺回扣篇 回扣3 数 列,共7页。
这是一份2023版考前三个月冲刺回扣篇 回扣3 数 列【无答案版】,共4页。
这是一份2023版考前三个月冲刺回扣篇 回扣1 非主干内容,共6页。学案主要包含了集合与常用逻辑用语,平面向量,不等式,复数等内容,欢迎下载使用。












