2023版考前三个月冲刺回扣篇　回扣6　解析几何【无答案版】

这是一份2023版考前三个月冲刺回扣篇　回扣6　解析几何【无答案版】，共5页。
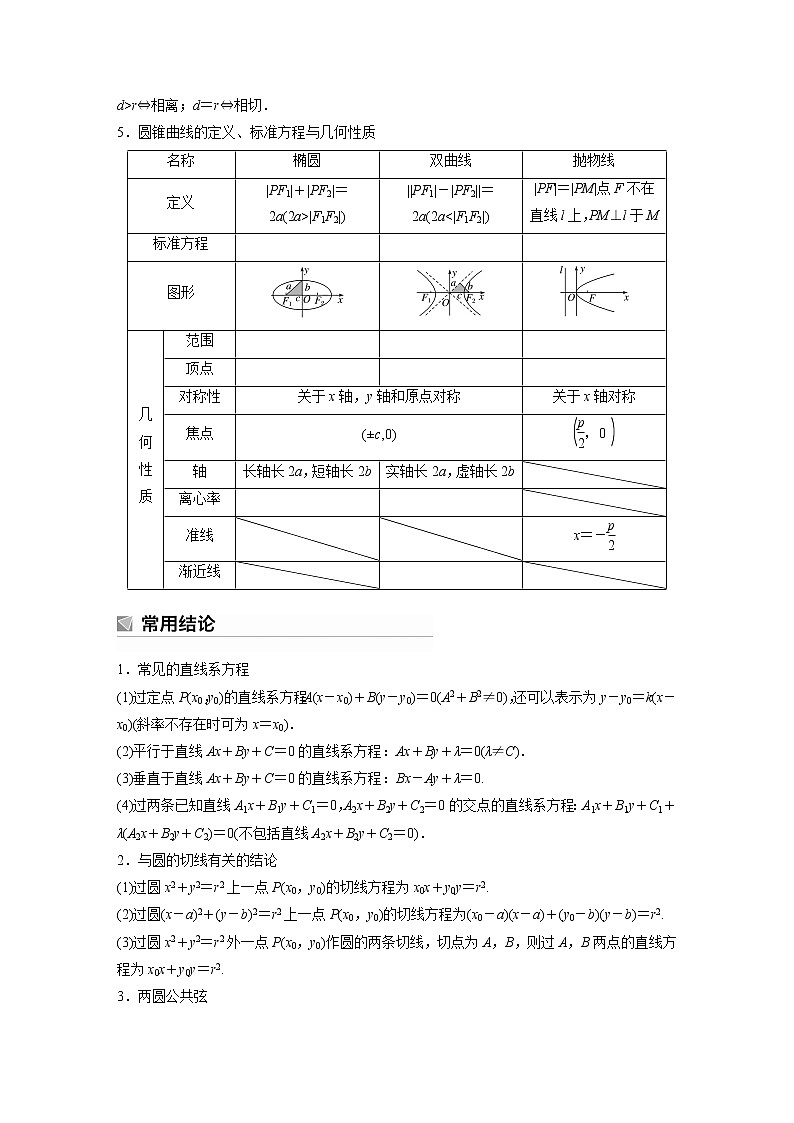
1．两条直线的位置关系
2.圆的三种方程
(1)圆的标准方程：(x－a)2＋(y－b)2＝r2(r>0)．
(2)圆的一般方程：x2＋y2＋Dx＋Ey＋F＝0(D2＋E2－4F>0)．
(3)圆的直径式方程：(x－x1)(x－x2)＋(y－y1)(y－y2)＝0(A(x1，y1)，B(x2，y2)是圆的直径的两端点)．
3．三种距离公式
(1)A(x1，y1)，B(x2，y2)两点的距离
|AB|＝________________________________________________________________________.
(2)点到直线的距离d＝________________________________________(其中点P(x0，y0)，直线方程为Ax＋By＋C＝0)．
(3)两平行线间的距离d＝________________________(其中两平行线方程分别为l1：Ax＋By＋C1＝0，l2：Ax＋By＋C2＝0)．
4．直线与圆的位置关系
直线l：Ax＋By＋C＝0和圆C：(x－a)2＋(y－b)2＝r2(r>0)有相交、相离、相切三种情况．可从代数和几何两个方面来判断：
(1)代数法(即判断直线与圆的方程联立所得方程组的解的情况)：Δ>0⇔相交；Δ0，b>0)，则渐近线的方程为eq \f(x2,a2)－eq \f(y2,b2)＝0，即y＝±eq \f(b,a)x.
(2)若渐近线的方程为y＝±eq \f(b,a)x，即eq \f(x,a)±eq \f(y,b)＝0，则双曲线的方程可设为eq \f(x2,a2)－eq \f(y2,b2)＝λ.
(3)若所求双曲线与双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1有公共渐近线，其方程可设为eq \f(x2,a2)－eq \f(y2,b2)＝λ(λ>0，焦点在x轴上；λ0)焦点F的弦，若A(x1，y1)，B(x2，y2)，α为直线AB的倾斜角，且y1>0>y2，则
(1)焦半径|AF|＝x1＋eq \f(p,2)＝eq \f(p,1－cs α)，
|BF|＝x2＋eq \f(p,2)＝eq \f(p,1＋cs α).
(2)x1x2＝eq \f(p2,4)，y1y2＝－p2.
(3)弦长|AB|＝x1＋x2＋p＝eq \f(2p,sin2α).
(4)eq \f(1,|FA|)＋eq \f(1,|FB|)＝eq \f(2,p).
(5)以弦AB为直径的圆必与准线相切．
(6)S△OAB＝eq \f(p2,2sin α)(O为抛物线的顶点)．
1．(2022·淄博模拟)已知条件p：直线x＋2y－1＝0与直线a2x＋(a＋1)y－1＝0平行，条件q：a＝1，则p是q的( )
A．充要条件
B．充分不必要条件
C．必要不充分条件
D．既不充分也不必要条件
2．已知圆C：x2＋y2＋2ay＝0(a>0)截直线eq \r(3)x－y＝0所得的弦长为2eq \r(3)，则圆C与圆C′：(x－1)2＋(y＋1)2＝1的位置关系是( )
A．相离 B．外切
C．相交 D．内切
3．设F1，F2分别是双曲线eq \f(x2,4)－eq \f(y2,45)＝1的左、右焦点，P是该双曲线上的一点，且3|PF1|＝5|PF2|，则△PF1F2的面积等于( )
A．14eq \r(3) B．7eq \r(15)
C．15eq \r(3) D．5eq \r(15)
4．(多选)(2022·南京模拟)已知抛物线y2＝4x的焦点为F，过原点O的动直线l交抛物线于另一点P，交抛物线的准线于点Q，下列说法正确的是( )
A．若O为线段PQ的中点，则|PF|＝2
B．若|PF|＝4，则|OP|＝2eq \r(5)
C．存在直线l，使得PF⊥QF
D．△PFQ面积的最小值为2
5．(多选)(2022·青岛模拟)已知椭圆C：eq \f(x2,4)＋eq \f(y2,3)＝1的左、右焦点分别是F1，F2，Meq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,3)，y0))为椭圆C上一点，则下列结论正确的是( )
A．△MF1F2的周长为6
B．△MF1F2的面积为eq \f(\r(15),3)
C．△MF1F2的内切圆的半径为eq \f(\r(15),9)
D．△MF1F2的外接圆的直径为eq \f(32,11)
6．已知抛物线y2＝4x的焦点为F，过点F的直线交抛物线于A，B两点，且|FA|·|FB|＝6，则|AB|＝________.
7．已知直线l过点P(0,1)，且与圆O：x2＋y2＝3相交于A，B两点，设eq \(OC,\s\up6(→))＝eq \(OA,\s\up6(→))＋eq \(OB,\s\up6(→))，若点C在圆O上，则直线l的倾斜角为________．
8．(2022·石家庄模拟)已知椭圆C1和双曲线C2有公共的焦点F1，F2，曲线C1和C2在第一象限相交于点P，且∠F1PF2＝60°.若椭圆C1的离心率的取值范围是eq \b\lc\[\rc\](\a\vs4\al\c1(\f(\r(3),3)，\f(\r(2),2)))，则双曲线C2的离心率的取值范围是________．
9．已知椭圆C：eq \f(y2,a2)＋eq \f(x2,b2)＝1(a>b>0)的离心率e＝eq \f(1,2)，左、右顶点分别为曲线y＝2x2－6与x轴的交点．
(1)求椭圆C的方程；
(2)过C的下焦点作一条斜率为k的直线l，l与椭圆C相交于点A与B，O为坐标原点，求△OAB面积的最大值．
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
10．已知双曲线C：eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的离心率是eq \f(\r(5),2)，实轴长是8.
(1)求双曲线C的方程；
(2)过点P(0,3)的直线l与双曲线C的右支交于不同的两点A和B，若直线l上存在不同于点P的点D满足|PA|·|DB|＝|PB|·|DA|成立，证明：点D的纵坐标为定值，并求出该定值．
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________
_______________________________________________________________________________斜截式
一般式
直线方程
y＝k1x＋b1，y＝k2x＋b2
A1x＋B1y＋C1＝0，
A2x＋B2y＋C2＝0
相交
k1≠k2
A1B2－A2B1≠0
垂直
k1k2＝－1
A1A2＋B1B2＝0
平行
k1＝k2且b1≠b2
eq \b\lc\{\rc\ (\a\vs4\al\c1(A1B2－A2B1＝0，,B1C2－B2C1≠0))或eq \b\lc\{\rc\ (\a\vs4\al\c1(A1B2－A2B1＝0，,A1C2－A2C1≠0))
重合
k1＝k2且b1＝b2
A1B2－A2B1
＝B1C2－B2C1
＝A1C2－A2C1＝0
名称
椭圆
双曲线
抛物线
定义
|PF1|＋|PF2|＝2a(2a>|F1F2|)
||PF1|－|PF2||＝2a(2a