




初中数学华师大版八年级下册第18章 平行四边形18.2 平行四边形的判定课文配套ppt课件
展开
这是一份初中数学华师大版八年级下册第18章 平行四边形18.2 平行四边形的判定课文配套ppt课件,共21页。PPT课件主要包含了逐点学练,本节小结,作业提升,学习目标,本节要点,学习流程,平行四边形的判定,知识点,感悟新知,对边关系等内容,欢迎下载使用。
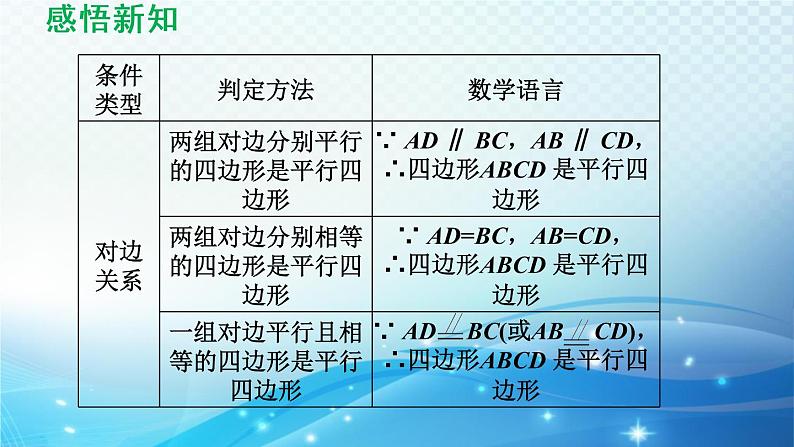
1. 判定方法: 判定平行四边形可以从对边、对角和对角线三个方面进行,如图18.2-1,在 ABCD 中,AC,BD 相交于点O,具体方法如下表所示.
2. 分式与分数、整式的关系:(1)分式中分母含有字母.由于字母可以表示不同的数,所以分式比分数更具有一般性. 分数是分式中字母取特定值时的特殊情况.(2)分式与整式的根本区别就是分式的分母中含有字母.3. 有理式:整式和分式统称有理式,即有理式
特别提醒1.平行四边形的判定定理和性质定理是互逆定理,解题时要注意区别,不能混淆.2.一组对边平行,另一组对边相等的四边形不一定是平行四边形.3.两组邻边分别相等的四边形不一定是平行四边形.
2. 灵活选择平行四边形判定定理的方法:(1)已知一组对边平行,可证明该组对边相等或证明另一组对边平行.(2)已知一组对边相等,可证明该组对边平行或证明另一组对边相等.(3)已知条件与对角线有关,可证明对角线互相平分.(4)已知条件与角有关,可证明两组对角分别相等或证明对边之间的关系.
如图18.2-2,已知BE ∥ DF,∠ ADF= ∠ CBE,AF=CE. 求证:四边形DEBF 是平行四边形.
解题秘方:紧扣条件“BE ∥ DF”需证明“BE=DF”或“DE ∥ BF”即可得到四边形DEBF 是平行四边形.
方法点拨:由边的关系判定平行四边形的基本思路1. 若已知一组对边平行,则可采用证这组对边相等或另一组对边平行这两种方法判定平行四边形;2. 若已知一组对边相等,则可采用证这组对边平行或另一组对边相等这两种方法判定平行四边形.
证明:∵ BE ∥ DF,∴∠ AFD= ∠ CEB.又∵∠ ADF= ∠ CBE,AF=CE,∴△ ADF ≌△ CBE(A. A. S.). ∴ DF=BE.又∵ BE ∥ DF,∴四边形DEBF 是平行四边形.
1-1. 如图, 已知△ ABC,分别以△ ABC的三边为边,在△ ABC的同侧作三个等边三角形: △ ABE,△ BCD,△ ACF. 求证: 四边形DEAF 是平行四边形.
∵△ACF是等边三角形,∴AC=AF.∴DE=AF.同理可得△ABC≌△FDC,∴DF=AB,∴DF=AE.∴四边形DEAF为平行四边形.
[中考·西宁] 如图18.2-3,在四边形ABCD 中,AC,BD 相交于点O,点O 是AC 的中点,AD ∥ BC,AC=8,BD=6.
解题秘方:紧扣对角线的关系判定平行四边形.
(1)求证:四边形ABCD 是平行四边形;
证明:∵点O 是AC 的中点,∴ OA=OC.∵ AD ∥ BC,∴∠ ADO= ∠ CBO.在△ AOD 和△ COB 中,∴△ AOD ≌△ COB(A. A. S.),∴ OD=OB.又∵ OA=OC,∴四边形ABCD 是平行四边形.
(2)若AC ⊥ BD,求ABCD 的面积.
解:∵四边形ABCD 是平行四边形,AC ⊥ BD,∴ S ABCD=2 S △ ABC=2× AC·BO= 2× AC· BD= AC·BD= ×8×6=24.
2-1. 如图,AC,BD 相交于点O,AB ∥ CD,AD ∥ BC,E,F 分别是OB,OD 的中点. 求证:四边形AFCE 是平行四边形.
相关课件
这是一份华师大版八年级下册第19章 矩形、菱形与正方形19.3 正方形集体备课课件ppt,共29页。PPT课件主要包含了逐点学练,本节小结,作业提升,学习目标,本节要点,学习流程,知识点,感悟新知,正方形的定义,正方形的性质等内容,欢迎下载使用。
这是一份华师大版七年级下册10.5 图形的全等图片课件ppt,共33页。PPT课件主要包含了逐点学练,本节小结,作业提升,学习目标,本节要点,学习流程,感悟新知,知识点,全等图形,①和⑥②③和⑤等内容,欢迎下载使用。
这是一份华师大版七年级下册第10章 轴对称、平移与旋转10.4 中心对称课文配套ppt课件,共27页。PPT课件主要包含了逐点学练,本节小结,作业提升,学习目标,本节要点,学习流程,感悟新知,知识点,中心对称图形,答案C等内容,欢迎下载使用。











