





所属成套资源:2023版考前三个月冲刺专题练
2023版考前三个月冲刺专题练 第18练 空间点、直线、平面之间的位置关系课件PPT
展开
这是一份2023版考前三个月冲刺专题练 第18练 空间点、直线、平面之间的位置关系课件PPT,共60页。PPT课件主要包含了PARTONE,专项典题精练,PARTTWO,练后疑难精讲,练后反馈,PARTTHREE,易错对点精补等内容,欢迎下载使用。
1.(2019·全国Ⅱ)设α,β为两个平面,则α∥β的充要条件是A.α内有无数条直线与β平行B.α内有两条相交直线与β平行C.α,β平行于同一条直线D.α,β垂直于同一平面
对于A,α内有无数条直线与β平行,当这无数条直线互相平行时,α与β可能相交,所以A不正确;对于B,根据两平面平行的判定定理与性质知,B正确;对于C,平行于同一条直线的两个平面可能相交,也可能平行,所以C不正确;对于D,垂直于同一平面的两个平面可能相交,也可能平行,如长方体的相邻两个侧面都垂直于底面,但它们是相交的,所以D不正确.
2.(多选)(2020·全国Ⅱ改编)设有下列四个命题,则下述命题是真命题的是A.两两相交且不过同一点的三条直线必在同一平面内B.过空间中任意三点有且仅有一个平面C.若空间两条直线不相交,则这两条直线平行D.若直线l⊂平面α,直线m⊥平面α,则m⊥l
A是真命题,两两相交且不过同一点的三条直线必定有三个交点,且这三个交点不在同一条直线上,由基本事实1“经过不在同一直线上的三个点,有且只有一个平面”,可知A为真命题;B是假命题,因为当空间中三点在一条直线上时,有无数个平面过这三个点;C是假命题,因为空间两条直线不相交时,它们可能平行,也可能异面;D是真命题,因为一条直线垂直于一个平面,那么它垂直于平面内的所有直线.
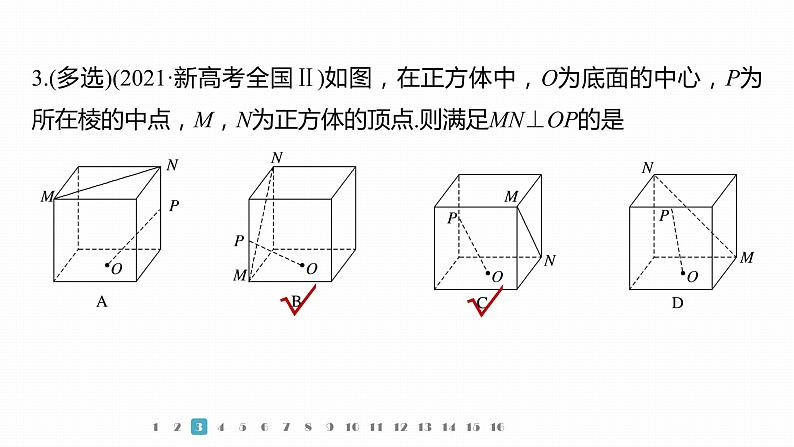
3.(多选)(2021·新高考全国Ⅱ)如图,在正方体中,O为底面的中心,P为所在棱的中点,M,N为正方体的顶点.则满足MN⊥OP的是
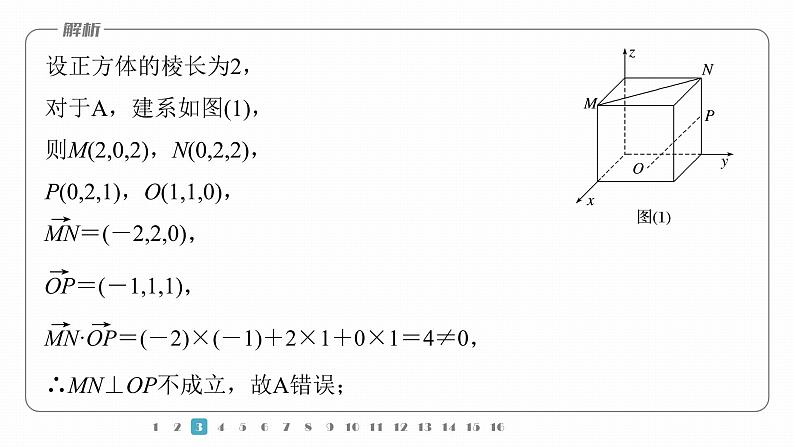
设正方体的棱长为2,对于A,建系如图(1),则M(2,0,2),N(0,2,2),P(0,2,1),O(1,1,0),
∴MN⊥OP不成立,故A错误;
对于B,建系如图(2),则M(2,0,0),N(0,0,2),P(2,0,1),O(1,1,0),
∴MN⊥OP,故B正确.同理可知,C正确,D错误.
4.(2019·全国Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线
取CD的中点O,连接ON,EO,如图所示.因为△ECD为正三角形,所以EO⊥CD,又平面ECD⊥平面ABCD,平面ECD∩平面ABCD=CD,所以EO⊥平面ABCD.设正方形ABCD的边长为2,
所以EN2=EO2+ON2=4,得EN=2.过M作CD的垂线,垂足为P,连接BP,
所以BM2=MP2+BP2
所以BM≠EN.连接BD,BE,因为四边形ABCD为正方形,所以N为BD的中点,即EN,MB均在平面BDE内,所以直线BM,EN是相交直线.
5.(2022·全国乙卷)在正方体ABCD-A1B1C1D1中,E,F分别为AB,BC的中点,则A.平面B1EF⊥平面BDD1B.平面B1EF⊥平面A1BDC.平面B1EF∥平面A1ACD.平面B1EF∥平面A1C1D
在正方体ABCD-A1B1C1D1中,AC⊥BD且DD1⊥平面ABCD,又EF⊂平面ABCD,所以EF⊥DD1,因为E,F分别为AB,BC的中点,所以EF∥AC,所以EF⊥BD,又BD∩DD1=D,BD,DD1⊂平面BDD1,所以EF⊥平面BDD1,
又EF⊂平面B1EF,所以平面B1EF⊥平面BDD1,故A正确;如图,以点D为原点,建立空间直角坐标系,设AB=2,则B1(2,2,2),E(2,1,0),F(1,2,0),B(2,2,0),A1(2,0,2),A(2,0,0),C(0,2,0),C1(0,2,2),
设平面B1EF的法向量为m=(x1,y1,z1),
可取m=(2,2,-1),同理可得平面A1BD的法向量为n1=(1,-1,-1),
平面A1AC的法向量为n2=(1,1,0),平面A1C1D的法向量为n3=(1,1,-1),则m·n1=2-2+1=1≠0,所以平面B1EF与平面A1BD不垂直,故B错误;因为m与n2不平行,所以平面B1EF与平面A1AC不平行,故C错误;因为m与n3不平行,所以平面B1EF与平面A1C1D不平行,故D错误.
6.(多选)(2021·新高考全国Ⅰ)在正三棱柱ABC-A1B1C1中,AB=AA1=1,点P满足 ,其中λ∈[0,1],μ∈[0,1],则A.当λ=1时,△AB1P的周长为定值B.当μ=1时,三棱锥P-A1BC的体积为定值
对于选项B,当μ=1时,点P在棱B1C1上运动,如图2所示,
对于选项C,取BC的中点D,B1C1的中点D1,连接DD1,A1B,
假设A1P⊥BP,则A1P2+BP2=A1B2,
解得μ=0或μ=1,所以点P与点D或D1重合时,A1P⊥BP;
方法一 对于选项D,易知四边形ABB1A1为正方形,所以A1B⊥AB1,设AB1与A1B交于点K,连接PK,要使A1B⊥平面AB1P,需A1B⊥KP,所以点P只能是棱CC1的中点,故选项D正确.方法二 对于选项D,分别取BB1,CC1的中点E,F,连接EF,则当μ= 时,点P在线段EF上运动,以点C1为原点建立如图所示的空间直角坐标系,则B(0,1,1),B1(0,1,0),
解得λ=1,所以只存在一个点P,使得A1B⊥平面AB1P,此时点P与F重合,故D正确.
7.(2022·全国乙卷)如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.
(1)证明:平面BED⊥平面ACD;
因为AD=CD,E为AC的中点,所以AC⊥DE.在△ADB和△CDB中,因为AD=CD,∠ADB=∠CDB,DB=DB,所以△ADB≌△CDB,所以AB=BC.因为E为AC的中点,所以AC⊥BE.又BE∩DE=E,BE,DE⊂平面BED,所以AC⊥平面BED,又AC⊂平面ACD,所以平面BED⊥平面ACD.
(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.
由(1)可知AB=BC,又∠ACB=60°,AB=2,所以△ABC为边长为2的正三角形,
因为AD=CD,AD⊥CD,所以△ADC为等腰直角三角形,所以DE=1.所以DE2+BE2=BD2,则DE⊥BE.由(1)可知,AC⊥平面BED.
连接EF,因为EF⊂平面BED,所以AC⊥EF,当△AFC的面积最小时,点F到直线AC的距离最小,即EF的长度最小.在Rt△BED中,当EF的长度最小时,
方法一 由(1)可知,DE⊥AC,BE⊥AC,所以EA,EB,ED两两垂直,以E为坐标原点,EA,EB,ED所在的直线分别为x,y,z轴建立如图所示的空间直角坐标系,则A(1,0,0),B(0, ,0),D(0,0,1),C(-1,0,0),
设平面ABD的法向量为n=(x1,y1,z1),
记CF与平面ABD所成的角为α,
方法二 因为E为AC的中点,所以点C到平面ABD的距离等于点E到平面ABD的距离的2倍.因为DE⊥AC,DE⊥BE,AC∩BE=E,AC,BE⊂平面ABC,所以DE⊥平面ABC.因为VD-AEB=VE-ADB,
因为AC⊥平面BED,EF⊂平面BED,所以AC⊥EF,
方法三 如图,过点E作EM⊥AB交AB于点M,连接DM,过点E作EG⊥DM交DM于点G. 因为DE⊥AC,DE⊥BE,AC∩BE=E,AC,BE⊂平面ABC,所以DE⊥平面ABC,又AB⊂平面ABC,所以DE⊥AB,又EM∩DE=E,EM,DE⊂平面DEM,所以AB⊥平面DEM,又EG⊂平面DEM,所以AB⊥EG,
又AB∩DM=M,AB,DM⊂平面ABD,所以EG⊥平面ABD,则EG的长度等于点E到平面ABD的距离.因为E为AC的中点,所以EG的长度等于点C到平面ABD的距离的 .
8.(2021·新高考全国Ⅰ)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:OA⊥CD;
因为AB=AD,O为BD的中点,所以OA⊥BD,又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,AO⊂平面ABD,所以AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
方法一 因为△OCD是边长为1的正三角形,且O为BD的中点,所以OC=OB=OD=1,
如图,过点E作EF∥AO,交BD于F,过点F作FG⊥BC,垂足为G,连接EG. 因为AO⊥平面BCD,所以EF⊥平面BCD,又BC⊂平面BCD,所以EF⊥BC,
又FG⊥BC,且EF∩FG=F,EF,FG⊂平面EFG,所以BC⊥平面EFG,则∠EGF为二面角E-BC-D的平面角,所以∠EGF=45°,则GF=EF.
因为FG⊥BC,CD⊥BC,所以GF∥CD,
方法二 如图所示,以O为坐标原点,OB,OA所在直线分别为x,z轴,在平面BCD内,以过点O且与BD垂直的直线为y轴建立空间直角坐标系.因为△OCD是边长为1的正三角形,且O为BD的中点,所以OC=OB=OD=1,
设A(0,0,a),a>0,
由题意可知平面BCD的法向量可取n=(0,0,1).设平面BCE的法向量为m=(x,y,z),
因为二面角E-BC-D的大小为45°,
得a=1,即OA=1,
9.(2022·咸阳模拟)已知m,n是不重合的直线,α,β,γ是不重合的平面,下列说法正确的是A.若α⊥γ,β⊥γ,则α∥βB.若m⊥α,n⊥α,则m⊥nC.若α∥β,γ∥β,则γ∥αD.若α⊥β,m⊥β,则m∥α
垂直于同一个平面的两个平面可以平行或相交,故A错误;垂直于同一个平面的两条直线平行,故B错误;若α∥β,γ∥β,则γ∥α,故C正确;若α⊥β,m⊥β,则m∥α或m⊂α,故D错误.
10.(多选)(2022·重庆模拟)如图,已知正方体ABCD-A1B1C1D1,P是棱CC1的中点,以下说法正确的是 A.过点P有且只有一条直线与直线AB,A1D1都相交B.过点P有且只有一条直线与直线AB,A1D1都平行C.过点P有且只有一条直线与直线AB,A1D1都垂直D.过点P有且只有一条直线与直线AB,A1D1所成角均为45°
过点P与直线AB相交的直线必在平面PAB内,过点P与直线A1D1相交的直线必在平面PA1D1内,故满足条件的直线必为两平面的交线,显然两平面有唯一交线,A正确;若存在一条直线与AB,A1D1都平行,则AB∥A1D1,矛盾,B不正确;因为A1D1∥AD,若l⊥A1D1则l⊥AD,若l⊥AB,则l⊥平面ABCD,显然满足条件的直线唯一,即CC1,C正确;取BB1,DD1的中点E,F,连接PE,PF,如图,则PE∥A1D1,PF∥AB,
若l与直线AB,A1D1所成角为45°,则l与PE,PF所成角为45°,显然∠EPF的角平分线及其外角平分线均符合题意,D不正确.
11.(多选)(2022·怀仁模拟)将正方形ABCD沿对角线BD翻折,使平面ABD与平面BCD的夹角为90°,则下列四个结论中正确的是A.AC⊥BDB.△ACD是等边三角形C.直线AB与平面BCD所成的角为D.AB与CD所成的角为
如图,取BD的中点E,连接AE,CE,则AE⊥BD,CE⊥BD,∵AE∩CE=E,AE,CE⊂平面AEC,∴BD⊥平面ACE,∵AC⊂平面ACE,∴BD⊥AC,故A正确;设折叠前正方形的边长为2,
∵平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,AE⊥BD,AE⊂平面ABD,∴AE⊥平面BCD,∴AE⊥CE,
即△ACD是等边三角形,故B正确;∵AE⊥平面BCD,
取BC的中点F,AC的中点G,连接EF,FG,EG,则EF∥CD,FG∥AB,∴∠EFG为异面直线AB,CD所成的角,
∴△EFG是等边三角形,
12.(多选)(2022·重庆质检)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点M在线段BC1(不包含端点)上运动,则下列结论正确的是 A.正方体ABCD-A1B1C1D1外接球的表面积为48πB.异面直线A1M与AD1所成角的取值范围是C.直线A1M∥平面ACD1D.三棱锥D1-AMC的体积随着点M的运动而变化
在正方体ABCD-A1B1C1D1中,AB与C1D1平行且相等,则四边形ABC1D1是平行四边形,AD1∥BC1,又△A1BC1是正三角形,A1M与BC1的夹角(锐角或直角)的范围是 ,因此B正确;由B知BC1∥AD1,而BC1⊄平面ACD1,AD1⊂平面ACD1,所以BC1∥平面ACD1,
同理A1B∥平面ACD1,又A1B∩BC1=B,A1B,BC1⊂平面A1BC1,所以平面A1BC1∥平面ACD1,而A1M⊂平面A1BC1,所以A1M∥平面ACD1,因此C正确;由BC1∥平面ACD1,因此随着点M的运动,点M到平面ACD1的距离不变,又△ACD1的面积为定值,所以 不变,因此D错误.
13.(2022·西安模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面四边形BCC1B1内(不含边界)一点,若A1P∥平面AEF,则线段A1P长度的取值范围是____________.
在正方体ABCD-A1B1C1D1中,分别取棱B1C1,BB1的中点M,N,连接A1M,MN,A1N,ME,BC1,如图,因为点E,F分别是棱BC,CC1的中点,则MN∥BC1∥EF,EF⊂平面AEF,MN⊄平面AEF,则有MN∥平面AEF,显然四边形BEMB1为矩形,有ME∥BB1∥AA1,ME=BB1=AA1,即有四边形AEMA1为平行四边形,则A1M∥AE,而AE⊂平面AEF,A1M⊄平面AEF,有A1M∥平面AEF,
又A1M∩MN=M,A1M,MN⊂平面A1MN,因此,平面A1MN∥平面AEF,因为A1P∥平面AEF,则有A1P⊂平面A1MN,又点P在平面BCC1B1上,平面A1MN∩平面BCC1B1=MN,从而得点P在线段MN上(不含端点),
14.(2022·南昌模拟)如图,四棱锥P-ABCD的底面是边长为1的正方形,点E是棱PD上一点,PE=3ED,若 且满足BF∥平面ACE,则λ=_____.
如图,连接BD,交AC于点O,连接OE,则BO=OD,在线段PE上取一点G使得GE=ED,
连接BG,FG,则BG∥OE,又因为OE⊂平面ACE,BG⊄平面ACE,所以BG∥平面ACE.因为BF∥平面ACE且满足BG∩BF=B,故平面BGF∥平面ACE.
因为平面PCD∩平面BGF=GF,平面PCD∩平面ACE=EC,则GF∥EC.
15.(2022·黄山检测)在矩形ABCD所在平面α的同一侧取两点E,F,使DE⊥α且AF⊥α,若AB=AF=3,AD=4,DE=1.
(1)求证:AD⊥BF;
∵四边形ABCD是矩形,∴AD⊥AB,又∵AF⊥α,∴AF⊥AD,又AF∩AB=A,AF,AB⊂平面ABF,∴AD⊥平面ABF,又∵BF⊂平面ABF,∴AD⊥BF.
(2)取BF的中点G,求证DF∥平面AGC;
连接BD交AC于点O,连接OG(图略),则OG是△BDF的中位线,OG∥DF,∵OG⊂平面AGC,DF⊄平面AGC,∴DF∥平面AGC.
(3)求多面体ABF-DCE的体积.
VABF-DCE=VF-ABCD+VE-FCD=VF-ABCD+VF-ECD
16.(2022·西宁模拟)如图,AB是圆O的直径,PA⊥圆O所在的平面,C为圆周上一点,D为线段PC的中点,∠CBA=30°,AB=2PA. (1)证明:平面ABD⊥平面PBC;
因为PA⊥圆O所在的平面,即PA⊥平面ABC,而BC⊂平面ABC,所以PA⊥BC,因为AB是圆O的直径,C为圆周上一点,所以AC⊥BC,又PA∩AC=A,PA,AC⊂平面PAC,所以BC⊥平面PAC,而AD⊂平面PAC,则BC⊥AD,
因为AC⊥BC,∠CBA=30°,所以AB=2AC,又AB=2PA,所以PA=AC,又D为线段PC的中点,所以AD⊥PC,又PC∩BC=C,PC,BC⊂平面PBC,所以AD⊥平面PBC,而AD⊂平面ABD,故平面ABD⊥平面PBC.
(2)若G为AD的中点,AB=4,求点P到平面BCG的距离.
由(1)得PA=AC,BC⊥平面PAC,CG⊂平面PAC,则BC⊥CG,BC⊥平面PCG,由题可知,G为AD的中点,AB=4,则PA=AC=2,
由于三棱锥P-BCG的体积等于三棱锥B-PCG的体积,
由于BC⊥平面PCG,
设点P到平面BCG的距离为d,由VP-BCG=VB-PCG,
考情分析高考必考内容,主要以几何体为载体考查空间点、线、面位置关系的判断,主要以选择题、填空题的形式出现,题目难度较小,或者以解答题的形式考查空间平行、垂直的证明,并与空间角的计算综合命题.
一、空间直线、平面位置关系的判定 核心提炼1.判断与空间位置关系有关的命题的方法:借助空间几何模型,如从长方体模型、四面体模型等模型中观察线面位置关系,结合有关定理,进行肯定或否定.2.两点注意:(1)平面几何中的结论不能完全引用到立体几何中.(2)当从正面入手较难时,可先假设结论成立,然后推出与题设或公认的结论相矛盾的命题,进而作出判断.
二、空间平行、垂直关系核心提炼1.直线、平面平行的判定定理及其性质定理(1)线面平行的判定定理:a⊄α,b⊂α,且a∥b⇒a∥α.(2)线面平行的性质定理:a∥α,a⊂β,α∩β=b⇒a∥b.(3)面面平行的判定定理:a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒β∥α.(4)面面平行的性质定理:α∥β,α∩γ=a,β∩γ=b⇒a∥b.
2.直线、平面垂直的判定定理及其性质定理(1)线面垂直的判定定理:m⊂α,n⊂α,m∩n=P,l⊥m,l⊥n⇒l⊥α.(2)线面垂直的性质定理:a⊥α,b⊥α⇒a∥b.(3)面面垂直的判定定理:a⊂β,a⊥α⇒α⊥β.(4)面面垂直的性质定理:α⊥β,α∩β=l,a⊂α,a⊥l⇒a⊥β.
三、空间直线、平面位置关系中的综合问题核心提炼1.处理空间点、直线、平面的综合问题,要认真审题,并仔细观察所给的图形,利用空间直线、平面平行与垂直的判定定理和性质定理求解.2.解决与折叠有关的问题的关键是弄清折叠前后的变化量和不变量,一般情况下,线段的长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的突破口.
1.[T3补偿](2022·北京模拟)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不垂直的是
如图1,因为M,N,Q为所在棱的中点,故由正方体的性质易得BB1⊥AB,CD⊥AB,MQ∥CD,MN∥BB1,所以MQ⊥AB,MN⊥AB,由于MQ∩MN=M,MQ,MN⊂平面MNQ,故AB⊥平面MNQ,故A不符合题意;如图2,因为M,N,Q为所在棱的中点,所以MN∥CD,MQ∥A1C,
由正方体的性质得AB1⊥CD,CD⊥BB1,AB1∩BB1=B1,AB1,BB1⊂平面ABB1,所以CD⊥平面ABB1,故CD⊥AB,所以MN⊥AB,同理得MQ⊥AB,MN∩MQ=M,MQ,MN⊂平面MNQ,故AB⊥平面MNQ,故B不符合题意;
如图3,因为M,N,Q为所在棱的中点,所以MN∥A1B1,AC∥A1B1,
故AB⊥平面MNQ不成立,故C符合题意;D选项同A选项,可判断AB⊥平面MNQ.
2.[T4补偿](2022·湖南师大附中模拟)已知E,F,G,H分别是三棱锥A-BCD的棱AB,AD,CD,CB上的点(不是顶点),则下列说法正确的是A.若直线EF,HG相交,则交点一定在直线BD上B.若直线EF,HG相交,则交点一定在直线AC上C.若直线EF,HG异面,则直线EF,HG中必有一条与直线BD平行D.若直线EF,HG异面,则直线EF,HG与直线BD分别相交
若直线EF,HG相交,设EF∩GH=P,则P∈EF,P∈GH,又EF⊂平面ABD,GH⊂平面BDC,所以P是平面ABD与平面CBD的公共点,则必在其交线BD上,即P∈BD,A正确,B错误;如图所示的情况满足EF,HG异面,但EF,HG均与BD相交,故C错误;当EF∥BD,且HG∩BD=P时,EF与HG异面,但EF与BD不相交,故D错误.
3.[T5补偿](多选)(2022·安庆模拟)已知ABCD-A1B1C1D1为正方体,P,Q,R分别为棱AD,A1B1,CC1的中点,则下列结论正确的是A.AB∥平面PQR B.AC∥平面PQRC.BP⊥QR D.BD1⊥平面PQR
取DC,B1C1,A1A的中点分别为L,M,N,连接LR,LP,RM,QM,QN,NP,由己知平面PQR即截面PLRMQN所在平面,其顶点分别为所在棱的中点,在△ACD中,PL为中位线,则AC∥PL,AC⊄平面PQR,PL⊂平面PQR,故AC∥平面PQR,三棱锥B-PQR为正三棱锥,故BP⊥QR.
因为AC⊥BD,AC⊥DD1,BD∩DD1=D,所以AC⊥平面BDD1,又BD1⊂平面BDD1,则AC⊥BD1.所以BD1⊥PL,同理可得BD1⊥RL,PL,RL⊂平面PQR,即可证得BD1⊥平面PQR.
4.[T12补偿](多选)(2022·太原模拟)如图,正方体ABCD-A1B1C1D1的棱长为a,E是棱DD1上的动点,则下列说法不正确的是 A.当E为DD1的中点时,直线B1E∥平面A1BDB.三棱锥C1-B1CE的体积为定值C.当E为DD1的中点时,B1E⊥BD1D.当E为DD1的中点时,直线B1E与平面CDD1C1所成的角正切值为
因为B1E⊂平面BDEB1,平面BDEB1∩平面A1BD=BD,若直线B1E∥平面A1BD,则由线面平行的性质可知,B1E∥BD,但是B1E与BD不平行,故A错误;
如图所示,当E为DD1的中点时,连接BD1交DB1于点O,若B1E⊥BD1,设垂足为F,
因为BB1
相关课件
这是一份2023版考前三个月冲刺专题练 第31练 数形结合思想课件PPT,共60页。PPT课件主要包含了专项典题精练,设Pxy,由图象可知,解得a=2,练后疑难精讲,练后反馈,易错对点精补,因为a·b=0,因为-6≤m≤6等内容,欢迎下载使用。
这是一份2023版考前三个月冲刺专题练 第26练 直线与圆锥曲线的位置关系课件PPT,共60页。PPT课件主要包含了PARTONE,专项典题精练,由①-②得,PARTTWO,练后疑难精讲,练后反馈,PARTTHREE,易错对点精补,两式相减得,因为PQ在椭圆上等内容,欢迎下载使用。
这是一份2023版考前三个月冲刺专题练 第32练 分类讨论思想课件PPT,共60页。PPT课件主要包含了专项典题精练,解得0m≤1,也是最小值,∵直线过12,∴1≤fx≤2,-∞4,又0ex1,可知f0=0,练后疑难精讲,练后反馈等内容,欢迎下载使用。









